Początki geometrii
Pierwszymi liniami, jakie człowiek sobie wyobraził, były linie proste i okręgi. To one wyznaczyły narodziny geometrii, co oznacza dosłownie „Pomiar Ziemi”, dając nam dokładne wyobrażenie o tym, do czego te linie były przeznaczone. Pierwszymi ekspertami od geometrii byli geodeci w starożytnym Egipcie. Grecy nazywali ich „arpedonapti” – ci, którzy wiążą liny. Egipscy eksperci zaciskali liny na ziemi, aby zaznaczyć linie i okręgi. Ślady tego starożytnego użycia są wciąż obecne w wielu współczesnych językach, jak na przykład w powiedzeniu „narysować linię”. Wykorzystanie lin do pomiarów ziemi pozostało niezmienione przez kilka stuleci i nadal można je znaleźć w pracy geodetów w stosunkowo niedawnych czasach.
Greccy historycy świadczą o narodzinach geometrii (dosłownie: Pomiar Ziemi) w Egipcie. Herodot mówi:
Jeżeli rzeka po prostu zniwelowała granice kawałka ziemi, rolą urzędników było przerysowanie dokładnych podziałów.
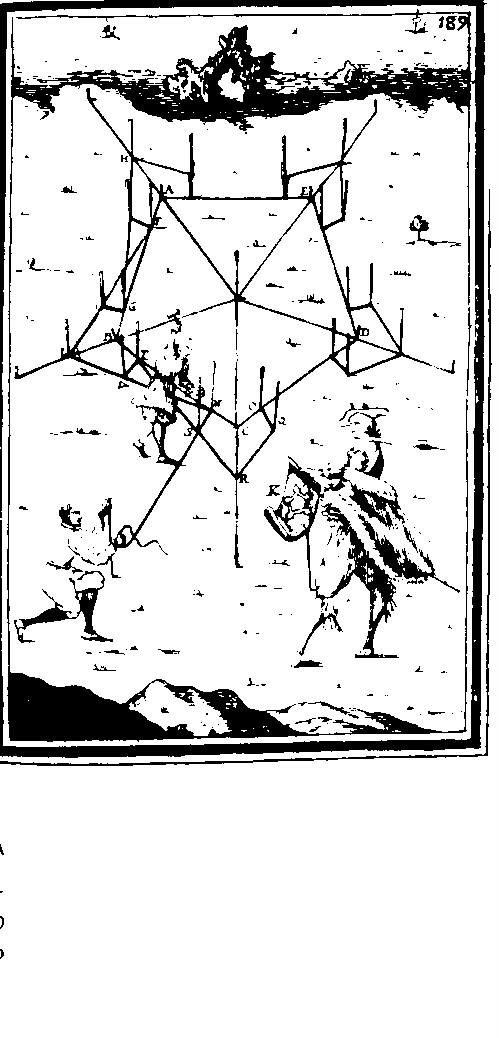 Egipskich ekspertów od geometrii nazywano „arpedonapti”, czyli tymi, którzy zawiązują liny. To właśnie poprzez zaciskanie sznurów rysowali dwie najprostsze i najważniejsze linie w geometrii: linię prostą i okrąg. Pierwsza z nich to po prostu napinanie liny między dwoma punktami, rodzaj operacji, której obraz jest wciąż obecny w wyrażeniach „rysować linię”, „rysować prostopadłą”; druga to obracanie jednego z dwóch punktów wokół drugiego, który jest nieruchomy. Czy mogli sobie wyobrazić zakres rozwoju tych dwóch elementarnych praktyk? Najprawdopodobniej nie. W rzeczywistości praktyczne potrzeby starożytnych mierniczych lądowych przypuszczalnie szybko spowodowały pojawienie się konieczności prac w rodzaju tych, które dziś nazywamy „z kwadratem i kompasem”, a które powinny być właściwie nazywane „z okręgami i liniami prostymi”.
Egipskich ekspertów od geometrii nazywano „arpedonapti”, czyli tymi, którzy zawiązują liny. To właśnie poprzez zaciskanie sznurów rysowali dwie najprostsze i najważniejsze linie w geometrii: linię prostą i okrąg. Pierwsza z nich to po prostu napinanie liny między dwoma punktami, rodzaj operacji, której obraz jest wciąż obecny w wyrażeniach „rysować linię”, „rysować prostopadłą”; druga to obracanie jednego z dwóch punktów wokół drugiego, który jest nieruchomy. Czy mogli sobie wyobrazić zakres rozwoju tych dwóch elementarnych praktyk? Najprawdopodobniej nie. W rzeczywistości praktyczne potrzeby starożytnych mierniczych lądowych przypuszczalnie szybko spowodowały pojawienie się konieczności prac w rodzaju tych, które dziś nazywamy „z kwadratem i kompasem”, a które powinny być właściwie nazywane „z okręgami i liniami prostymi”.
W dzisiejszych czasach tak naturalnie uważamy papier za naturalną arenę geometrii, że użycie samych tylko kwadratów i kompasów uważamy za arbitralne ograniczenie wprowadzone przez spekulatywne duchy, które przedkładały kilka liczb aksjomatów nad wielość wygód płynących z wielości instrumentów. W konsekwencji różnica między teoretycznym geometrą – mówię oczywiście o klasycznym, euklidesowym – a technikiem – tym, który mierzy, architektem – polega głównie na tym, że ten pierwszy decyduje się dobrowolnie nie używać instrumentów, kwadratów i pantografów, które ten drugi wykorzystuje na swoją korzyść.
W ten sposób mamy tendencję do całkowitego ignorowania geometrii „w terenie” na rzecz tej „na papierze”, nie dostrzegając, że kiedy przenosimy operacje geometryczne z terenu na papier, będą one wymagały niekiedy zupełnie innych technik i metod.
Nie należy pomijać faktu, że precyzja planu jest o wiele bardziej potrzebna w terenie (zarówno temu, który mierzy i dzieli na części kawałek ziemi, jak i architektowi, który tworzy budynki – najczęściej są to dwie te same osoby -) niż na papierze. Architekt, który ma jasne wyobrażenie o ogólnym planie i pamięta proces, który wykonał, aby przez niego przejść, potrzebowałby szkicu. Stosunkowo niedawne, jak również stare mapy, które, siłą rzeczy, zostały sporządzone przy użyciu skromnych instrumentów i pomocy, nie odtwarzają dokładnie granic kawałka ziemi. W rzeczywistości jest to niemożliwe, ponieważ nawet błąd o jeden punkt procentowy – najmniejszy, jaki mógłby się zdarzyć w dość dużej skali – rodziłby absolutny błąd, który trudno byłoby zaakceptować w terenie. W tym przypadku znajomość formy i miar obiektu, który ma być opisany (pole, budynek), jest fundamentalna; to od eksperta geometrii będzie zależało, czy odtworzy na polu precyzję, której brakuje na papierze. To samo dzieje się z matematykiem, dla którego dokładność figur nie jest wcale przydatna w demonstracjach. Geometria na papierze zastępuje precyzję operacji w terenie, geometrią procesu myślowego.
Przeciwnie, od logiki do materialnej dokładności, jako konsekwencja koniecznego powiększenia skali, aby przejść od planu do jego rzeczywistego stworzenia, czynność napinania liny pozostała jedną z głównych operacji od czasów starożytnego Egiptu i starożytnej Grecji. Praktyka ta przetrwała aż do czasów współczesnych, wyprzedzona jedynie przez wynalezienie i udoskonalenie niektórych instrumentów optycznych. Podczas gdy na papierze dość łatwo jest narysować prostopadłą za pomocą linijki i kwadratów, ta sama operacja na polu, z tym samym stopniem dokładności, wymaga radykalnie innych metod. W terenie kwadrat jest bezużyteczny, ponieważ jest zbyt mały w stosunku do wymiarów form. Nawet jeśli kwadrat jest niezwykle precyzyjny, to prostopadła, którą może wyznaczyć, będzie sięgała najwyżej mniej więcej metra. Jeżeli mamy wyznaczyć kwadrat o boku 30 metrów, to musimy przedłużyć tę linię 30 razy. Byłaby to operacja tak niedokładna, że prawdopodobnie dałaby takie same wyniki, jak gdybyśmy zmierzyli kąt prosty w przybliżeniu.
 Te rozważania sprowadzają nas z powrotem do początkowego pytania: jakich technik używali egipscy mierniczy do wyznaczenia kwadratowego kawałka ziemi? W jaki sposób uzyskiwali oni kąt kwadratowy?
Te rozważania sprowadzają nas z powrotem do początkowego pytania: jakich technik używali egipscy mierniczy do wyznaczenia kwadratowego kawałka ziemi? W jaki sposób uzyskiwali oni kąt kwadratowy?
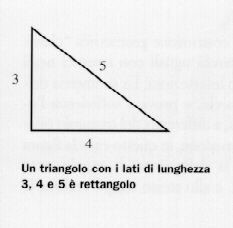
Jak sugerują niektórzy uczeni, jest możliwe, że znali twierdzenie Pitagorasa (VI w. p.n.e.) lub, dokładniej, mieli świadomość jego przeciwieństwa, to znaczy faktu, że trójkąt o bokach długości 3, 4 i 5, w którym kwadrat dłuższego boku jest równy sumie kwadratów dwóch pozostałych boków, jest trójkątem prostokątnym. Jeśli zatem rozciągniemy linę pierścieniową do długości 12 jednostek, oznaczoną w trzech punktach w odległości 3, 4 i 5, w kierunku kształtu trójkąta o wierzchołku w oznaczonych punktach, to kąt między najkrótszymi bokami trójkąta jest kątem prostym.
Nie wiadomo, czy to był proces starożytnych geodetów ziemi używane intheir czas jak nie zostało udowodnione, że starożytni Egipcjanie wiedział, że thetriangle z boków 3, 4 i 5 jest prawo kąt trójkąt. Nawet jeśli wiedzieli o tym, lub o innych trójkątach pitagorejskich (co jest silnie sugerowane przez obecność kilku trójkątów pitagorejskich, jeśli nie w matematyce egipskiej, to w babilońskiej), to implikuje to, że znali naturę lub przynajmniej wiedzieli, jak stworzyć kąt prosty.
Skąd ta wiedza pochodzi? Ze względu na brak choćby częściowej dokumentacji i świadków, możemy spróbować podejść do problemu z innego punktu widzenia, bardziej matematycznego niż historycznego. Pytanie, które musimy postawić, brzmi: co odróżnia kąt prosty od innych? Albo lepiej: na czym polega osobliwość kąta trójkąta o bokach 3, 4 i 5?
Natychmiastowa odpowiedź brzmi: w przeciwieństwie do innych trójkątów, pitagorejskie, a w szczególności najprostszy z nich, ten o bokach 3, 4 i 5, można dopasować do siebie, obracając je z jednej strony, a następnie z drugiej. W ten sposób uzyskuje się symetryczną konfigurację, która całkowicie wypełnia całą dostępną przestrzeń, bez zachodzenia na siebie i bez przerw.
 Żaden inny kąt oprócz kąta prostego nie ma tej cechy symetrii, która doczekała się własnej definicji w pierwszej kompletnej książce o geometrii, która dotarła do naszych czasów, Elementach Euklidesa (IV w. p.n.e.):
Żaden inny kąt oprócz kąta prostego nie ma tej cechy symetrii, która doczekała się własnej definicji w pierwszej kompletnej książce o geometrii, która dotarła do naszych czasów, Elementach Euklidesa (IV w. p.n.e.):
Gdy prosta padająca na inną tworzy równe kąty, to obie są proste.
Natura kąta kwadratowego polega na tym, że kąty powstałe w wyniku przecięcia dwóch prostych są równe. Można to natychmiast udowodnić na papierze, składając papier wzdłuż jednej ze zbiegających się linii i sprawdzając, czy druga linia się na nim rozkłada.
„Klasyczna” konstrukcja geometryczna, która polega na zakreśleniu dwóch okręgów, a następnie zjednoczeniu ich przecięć, również posiada tę własność.Symetryczny charakter formy jest dość oczywisty i jest to wyraźny dowód na równość kątów. Ponadto, w przeciwieństwie do trójkąta pitagorejskiego, który wymaga dalszej konstrukcji, w tym przypadku forma od razu sugeruje definicję kąta kwadratowego poprzez równość kątów i jednocześnie sama się konstruuje.
Są to wciąż proste przypuszczenia. Bez wątpienia proces ten jest zdecydowanie prostszy i bardziej precyzyjny niż ten pierwszy. Można by powiedzieć, że w ten sposób możemy wyznaczyć tylko prostopadłą przechodzącą przez środek danego odcinka, zwaną też osią odcinka. Nietrudno jednak zauważyć, że jeśli potrzebujemy prostopadłej na jednym z krańców, jak w przypadku rysowania kwadratu, konieczne będzie podwojenie odcinka przedłużając go w kierunku miejsca, gdzie chcemy narysować prostopadłą, a następnie powtórzenie poprzedniego procesu. Należy zauważyć, że wszystkie te techniki szczególnie dobrze sprawdzają się na terenach płaskich, takich jak równina egipska.