Porządek operacji: PEMDAS

PEMDASExamplesAn Issue

Purplemath

Jeśli zostaniesz poproszony o uproszczenie czegoś takiego jak „4 + 2×3”, pytanie, które naturalnie się pojawia, brzmi: „Którędy mam to zrobić? Bo są dwie opcje!” Mógłbym najpierw dodać:

…lub mógłbym najpierw pomnożyć:

Która odpowiedź jest właściwa?

MathHelp.com

Affiliate

Aby wyeliminować to zamieszanie, mamy pewne zasady pierwszeństwa, ustanowione co najmniej tak daleko jak w latach 1500, zwane „kolejnością operacji”. Operacje” to dodawanie, odejmowanie, mnożenie, dzielenie, wykładanie i grupowanie; „kolejność” tych operacji określa, które operacje mają pierwszeństwo (są załatwiane) przed którymi innymi operacjami.

Powszechną techniką zapamiętywania kolejności operacji jest skrót (lub, bardziej poprawnie, „akronim”) „PEMDAS”, który jest przekształcany w wyrażenie mnemoniczne „Please Excuse My Dear Aunt Sally”. To wyrażenie oznacza, i pomaga zapamiętać kolejność „nawiasów, wykładników, mnożenia i dzielenia oraz dodawania i odejmowania”. Ta lista mówi o kolejności operacji: Nawiasy wyprzedzają wykładniki, które wyprzedzają mnożenie i dzielenie (ale mnożenie i dzielenie są na tej samej randze), a mnożenie i dzielenie wyprzedzają dodawanie i odejmowanie (które są razem na najniższej randze). Innymi słowy, pierwszeństwo jest następujące:

Gdy masz kilka operacji tej samej rangi, po prostu działasz od lewej do prawej. Na przykład, 15 ÷ 3 × 4 nie jest 15 ÷ (3 × 4) = 15 ÷ 12, ale jest raczej (15 ÷ 3) × 4 = 5 × 4, ponieważ, idąc od lewej do prawej, najpierw dochodzimy do znaku dzielenia.

Jeśli nie jesteś tego pewien, przetestuj to w swoim kalkulatorze, który został zaprogramowany z hierarchią kolejności operacji. Na przykład, wpisując powyższe wyrażenie do kalkulatora graficznego, otrzymasz:

Używając powyższej hierarchii, widzimy, że w pytaniu „4 + 2×3” na początku tego artykułu, wybór 2 był poprawną odpowiedzią, ponieważ musimy wykonać mnożenie przed wykonaniem dodawania.

(Uwaga: Osoby posługujące się brytyjskim językiem angielskim często używają akronimu „BODMAS” zamiast „PEMDAS”. BODMAS to skrót od „Brackets, Orders, Division and Multiplication, and Addition and Subtraction” (nawiasy, polecenia, dzielenie i mnożenie, dodawanie i odejmowanie). Ponieważ „nawiasy” to to samo co nawiasy, a „rzędy” to to samo co wykładniki, te dwa akronimy oznaczają to samo. Ponadto, można zauważyć, że „M” i „D” są odwrócone w wersji brytyjsko-angielskiej; to potwierdza, że mnożenie i dzielenie są na tym samym „poziomie” lub „randze”. Kanadyjscy użytkownicy języka angielskiego rozróżniają je, używając BEDMAS.)

Porządek operacji został ustalony w celu uniknięcia błędnej komunikacji, ale PEMDAS może generować własne zamieszanie; niektórzy uczniowie czasami mają tendencję do stosowania hierarchii tak, jakby wszystkie operacje w problemie były na tym samym „poziomie” (po prostu idąc od lewej do prawej), ale często te operacje nie są „równe”. Często pomaga to pracować z problemem od środka na zewnątrz, a nie od lewej do prawej, ponieważ często niektóre części problemu są „głębiej” niż inne. Najlepszym sposobem, aby to wyjaśnić jest kilka przykładów:

• Uprość 4 + 32.

• Uprościć 4 + (2 + 1)2.

Muszę uprościć wewnątrz nawiasów, zanim będę mógł wziąć wykładnik przez. Dopiero wtedy mogę wykonać dodawanie 4.

4 + (2 + 1)2 = 4 + (3)2 = 4 + 9 = 13

Ogłoszenie

• Uprościć 4 + 2.

Affiliate

Nie powinienem próbować robić tych zagnieżdżonych nawiasów od lewej do prawej; ta metoda jest po prostu zbyt podatna na błędy. Zamiast tego postaram się pracować od środka na zewnątrz. Najpierw uproszczę wnętrze nawiasów krzywych, następnie uproszczę wnętrze nawiasów kwadratowych, a dopiero potem zajmę się dzieleniem na kwadraty. Po wykonaniu tych czynności mogę w końcu dodać 4:

4 + 2

= 4 + 2

= 4 + 2

= 4 + 9

= 13

Nie ma żadnego szczególnego znaczenia w użyciu nawiasów kwadratowych (the „” powyżej) zamiast nawiasów. Nawiasy i nawiasy klamrowe (znaki „{” i „}”) są używane, gdy istnieją zagnieżdżone nawiasy, jako pomoc w śledzeniu, które nawiasy idą z którymi. Różne znaki grupujące są używane tylko dla wygody. Jest to podobne do tego, co dzieje się w arkuszu kalkulacyjnym Excel, gdy wprowadzasz formułę z użyciem nawiasów: każdy zestaw nawiasów jest oznaczony kolorem, dzięki czemu można odróżnić pary:



• Uproszczenie

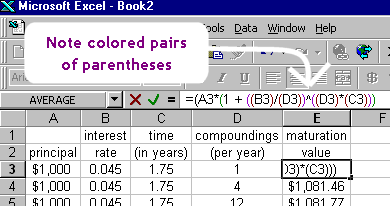
W pierwszej kolejności uproszczę wewnątrz nawiasów:

Więc moja uproszczona odpowiedź brzmi

Następna strona ma więcej działających przykładów przykładów….

URL: https://www.purplemath.com/modules/orderops.htm

Strona 1Strona 2Strona 3

Wykonawca: Zamawiający.