Analiza korelacji lub prosta analiza regresji liniowej może określić, czy dwie zmienne numeryczne są znacząco liniowo powiązane. Analiza korelacji dostarcza informacji o sile i kierunku liniowej zależności między dwiema zmiennymi, podczas gdy prosta analiza regresji liniowej szacuje parametry w równaniu liniowym, które może być użyte do przewidywania wartości jednej zmiennej na podstawie drugiej.
Korelacja
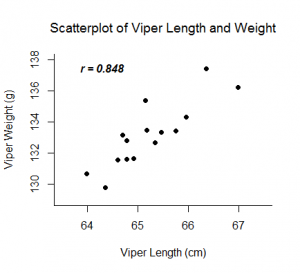
Współczynnik korelacji Pearsona, r, może przyjmować wartości między -1 a 1. Im bardziej r jest oddalone od zera, tym silniejsza jest liniowa zależność między dwiema zmiennymi. Znak r odpowiada kierunkowi związku. Jeżeli r jest dodatnie, wówczas wraz ze wzrostem jednej zmiennej wzrasta tendencja drugiej. Jeśli r jest ujemne, to wraz ze wzrostem jednej zmiennej, druga ma tendencję do zmniejszania się. Doskonała zależność liniowa (r=-1 lub r=1) oznacza, że jedna ze zmiennych może być doskonale wyjaśniona przez liniową funkcję drugiej.
Przykłady:

Regresja liniowa
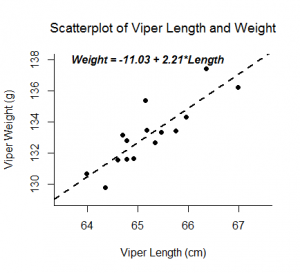
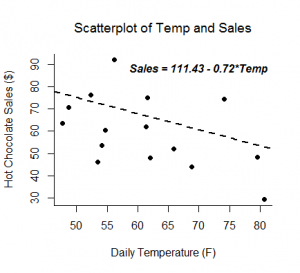
Analiza regresji liniowej pozwala uzyskać oszacowania dla nachylenia i przechyłu równania liniowego przewidującego zmienną wynikową, Y, na podstawie wartości zmiennej predykcyjnej, X. Ogólna postać tego równania jest przedstawiona poniżej:
![]()
Przecinek, b0, jest przewidywaną wartością Y, gdy X=0. Nachylenie, b1, jest średnią zmianą w Y dla każdego wzrostu X o jedną jednostkę. Poza podaniem siły i kierunku liniowej zależności między X i Y, oszacowanie nachylenia pozwala na interpretację, jak Y zmienia się, gdy X wzrasta. Równanie to może być również użyte do przewidywania wartości Y dla wartości X.
Przykłady:
Wnioskowanie
Testy inferencyjne można przeprowadzić zarówno na korelacji, jak i na szacunkach nachylenia obliczonych na podstawie losowej próbki z populacji. Obie analizy są testami t na hipotezie zerowej, że dwie zmienne nie są liniowo powiązane. W przypadku przeprowadzenia na tych samych danych, test korelacji i test nachylenia dają tę samą statystykę testową i wartość p-value.
Założenia:
- Próba losowa
- Niezależne obserwacje
- Zmienna przewidywana i zmienna wyniku są liniowo powiązane (oceniane przez wizualne sprawdzenie wykresu rozrzutu).
- Populacja wartości dla wyniku jest normalnie rozłożona dla każdej wartości predyktora (oceniana przez potwierdzenie normalności reszt).
- Wariantancja rozkładu wyniku jest taka sama dla wszystkich wartości predyktora (oceniana przez wizualne sprawdzenie wykresu reszt dla wzoru lejka).
Hypotezy:
Ho: Dwie zmienne nie są liniowo powiązane.
Ha: Dwie zmienne są powiązane liniowo.
Relewantne równania:
Stopnie swobody: df = n-2


![]()
Przykład 1: Obliczanie ręki
Te filmy badają liniową zależność między wysokością ludzi a pomiarami rozpiętości ramion.
Korelacja:


Regresja:


Przykładowy wniosek: Badając zależność między rozpiętością ramion a wzrostem, stwierdzamy dużą korelację dodatnią (r=.95), wskazującą na silną dodatnią zależność liniową między tymi dwiema zmiennymi. Obliczyliśmy równanie dla linii najlepszego dopasowania jako Armspan=-1.27+1.01(Wysokość). Oznacza to, że dla osoby, która ma zero cali wzrostu, przewidywana rozpiętość ramion wynosiłaby -1,27 cala. Nie jest to możliwa wartość, ponieważ zakres naszych danych będzie znacznie wyższy. Na każdy wzrost wzrostu o 1 cal przewiduje się wzrost rozpiętości ramion o 1,01 cala.
Przykład 2: Przeprowadzanie analizy w programie Excel 2016
Niektóre z tych analiz wymagają włączenia dodatku Data Analysis ToolPak w programie Excel. Aby uzyskać instrukcje dotyczące przeprowadzania tej analizy w poprzednich wersjach programu Excel, odwiedź stronę https://stat.utexas.edu/videos
Zbiór danych wykorzystany w filmach
Macierz korelacji i wartość p:
Kierunki PDF odpowiadające wideo
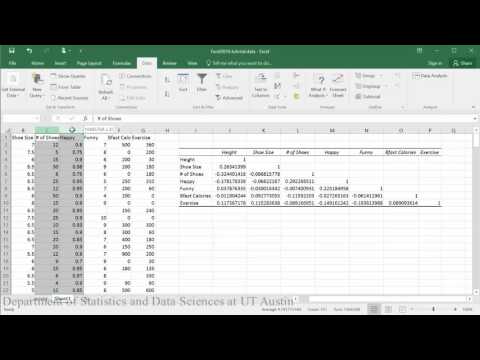

Tworzenie wykresów rozrzutu:
Kierunki PDF odpowiadające materiałowi wideo
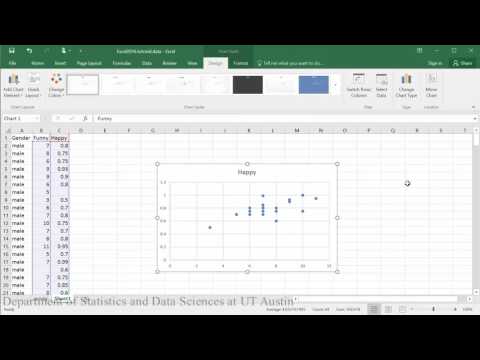

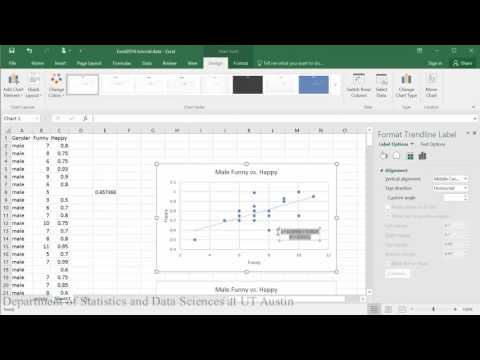
Model liniowy (pierwsza połowa samouczka):
PDF wskazówki odpowiadające filmowi

Tworzenie wykresów reszt:
PDF wskazówki odpowiadające filmowi
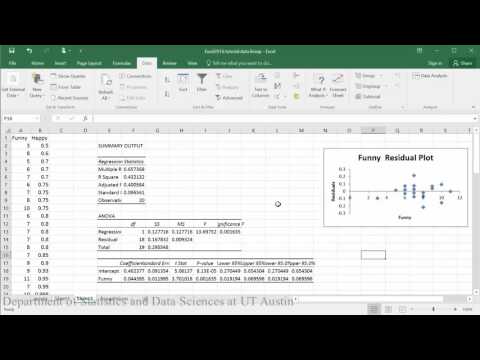

Przykładowy wniosek: Oceniając zależność między tym, jak szczęśliwy jest ktoś, a tym, jak zabawni oceniają go inni, wykres rozrzutu wskazuje, że wydaje się, iż istnieje umiarkowanie silna dodatnia zależność liniowa między tymi dwiema zmiennymi, co potwierdza współczynnik korelacji (r = .65). Sprawdzenie założeń za pomocą wykresu reszt nie wykazało żadnych problemów z danymi. Równanie liniowe dla przewidywania happy from funny było Happy=.04+0.46(Funny). Punkt przecięcia y wskazuje, że dla osoby, której ocena śmieszności wynosi zero, przewidywane szczęście wynosi 0,04. Ocena śmieszności istotnie przewiduje szczęście, tak że dla każdego wzrostu śmieszności o 1 punkt przewiduje się wzrost szczęścia o .46 (t = 3.70, p = .002).
Przykład 3: Wykonywanie analizy w R
Następujące filmy badają związek między BMI i ciśnieniem krwi dla próbki pacjentów medycznych.
Zbiór danych wykorzystany w filmach
Korelacja:
Plik skryptowy R wykorzystany w filmie

Regresja:
Plik skryptowy R wykorzystany w filmie