Matematyka | Średnia, wariancja i odchylenie standardowe

Średnia to średnia z danego zestawu danych. Rozważmy poniższy przykład

Te osiem punktów danych ma średnią 5:

$^frac{2 + 4 + 4 + 4 + 5 + 5 + 7 + 9}{8} = 5.$

$Formuła : \μ = średnia, a x1, x2, x3...., xi są elementami.Zauważ też, że średnia jest czasem oznaczana przez$

Wariancja to suma kwadratów różnic między wszystkimi liczbami i średnimi.
Odchylenie dla powyższego przykładu. Najpierw oblicz odchylenia każdego punktu danych od średniej, a następnie podnieś do kwadratu wynik każdego z nich:

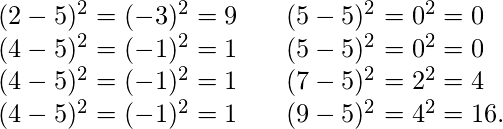
$\begin{array}{llll} (2-5)^2 = (-3)^2 = 9 (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 (7-5)^2 = 2^2 = 4 \\ (4-5)^2 = (-1)^2 = 1 (9-5)^2 = 4^2 = 16. \\ end{array}$

variance = $frac{9 + 1 + 1 + 1 + 0 + 0 + 4 + 16}{8}$ = 4.

$Formuła: \sigma^{2}= \frac { \sum_{i=1}^{N} (x_{i}-}mu)^{2}}{N}$

Gdzie μ jest średnią, N jest całkowitą liczbą elementów lub częstością rozkładu.

Odchylenie standardowe jest pierwiastkiem kwadratowym z wariancji. Jest to miara stopnia, w jakim dane różnią się od średniej.

Odchylenie standardowe (dla powyższych danych) = $\sqrt{ 4 }$ = 2

Dlaczego matematycy wybrali kwadrat, a następnie pierwiastek kwadratowy, aby znaleźć odchylenie, dlaczego nie po prostu wziąć różnicę wartości?
Jednym z powodów jest suma różnic staje się 0 zgodnie z definicją średniej. Suma różnic bezwzględnych może być opcja, ale z różnic bezwzględnych, to było trudne do udowodnienia wielu ładne twierdzenia.

$textup{Współczynnik zmienności } =\Odchylenie standardowe}}{Mean}*100$

Wartość odchylenia standardowego wynosi 0, jeśli wszystkie wartości w zbiorze wejściowym są takie same.
Jeśli dodamy (lub odejmiemy) liczbę powiedzmy 7 do wszystkich wartości w zbiorze wejściowym, średnia wzrośnie (lub zmaleje) o 7, ale odchylenie standardowe się nie zmieni.
Jeśli pomnożymy wszystkie wartości w zbiorze wejściowym przez liczbę 7, zarówno średnia, jak i odchylenie standardowe są pomnożone przez 7. Ale jeśli pomnożymy wszystkie wartości wejściowe przez liczbę ujemną, powiedzmy -7, średnia jest pomnożona przez -7, ale odchylenie standardowe jest pomnożone przez 7.
Odchylenie standardowe i wariancja są miarą, która mówi, jak rozłożone są liczby. Podczas gdy wariancja daje przybliżone wyobrażenie o rozprzestrzenianiu się, odchylenie standardowe jest bardziej konkretne, dając dokładne odległości od średniej.
Średnia, mediana i tryb są miarą tendencji centralnej danych (zgrupowanych lub niezgrupowanych).

Poniższe pytania zostały zadane w poprzednich latach egzaminów GATE
http://quiz.geeksforgeeks.org/gate-gate-cs-2012-question-64/

GeeksforGeeks

Dodaj komentarz Anuluj pisanie odpowiedzi