Quão forte é a encriptação de 256-bit?

“Diz “força de encriptação de 256-bit… isso é bom?”

A maioria das pessoas vê o termo encriptação de 256-bit banalizado a toda a hora e – se estivermos a ser honestos – não fazem a menor ideia do que significa ou de quão forte é. Uma vez ultrapassado o nível da superfície, “codifica os dados e torna-os ilegíveis”, a encriptação é um assunto incrivelmente complicado. Não é uma leitura leve. A maioria de nós não guarda um livro sobre exponenciação modular na mesa final ao lado das camas.

É por isso que é compreensível que haja alguma confusão quando se trata de forças de encriptação, o que significam, o que é “bom”, etc. Não há falta de perguntas sobre encriptação – especificamente sobre encriptação de 256 bits.

Chefe entre eles: Quão forte é a encriptação de 256-bit?

Então, hoje vamos falar apenas sobre isso. Vamos cobrir o que é um pouco de segurança, vamos entrar na forma mais comum de encriptação de 256 bits e vamos falar sobre o que seria necessário para decifrar a encriptação com essa força.

Vamos tirar o hash.

Uma rápida actualização da encriptação, em geral

Quando se encripta algo, está-se a pegar nos dados não encriptados, chamados plaintextos, e a executar uma função algorítmica para criar um pedaço de texto criptografado. O algoritmo que está a utilizar chama-se a chave. Com a excepção das chaves públicas em cifragem assimétrica, o valor da chave de encriptação precisa de ser mantido em segredo. A chave privada associada a essa peça de texto criptográfico é o único meio prático de a decifrar.

Agora, tudo isso soa incrivelmente abstracto, por isso vamos usar um exemplo. E vamos deixar Bob e Alice fora disto, pois estão ocupados a explicar a encriptação em literalmente todos os outros exemplos na Internet.

Vamos com Jack e Diane, e digamos que Jack quer enviar a Diane uma mensagem que diz: “Oh sim, a vida continua”.

Jack vai levar a sua mensagem e vai usar um algoritmo ou cifra – a chave de encriptação – para codificar a mensagem em texto criptografado. Agora ele vai passá-la a Diane, juntamente com a chave, que pode ser usada para decifrar a mensagem para que seja legível novamente.

Enquanto mais ninguém deitar as mãos à chave, o texto cifrado não vale nada porque não pode ser lido.

Como funciona a encriptação moderna?

Jack e Diane acabam de demonstrar a encriptação na sua forma mais básica. E embora a matemática utilizada nas cifras primitivas fosse bastante simples -como o facto de ter de ser executada por um humano – o advento da informática aumentou a complexidade da matemática que está na base dos sistemas de criptografia modernos, mas os conceitos continuam a ser em grande parte os mesmos.

Uma chave, ou algoritmo específico, é utilizada para encriptar os dados, e só outra parte com conhecimento da chave privada associada pode decifrar.

Neste exemplo, em vez de uma mensagem escrita que opina sombriamente que a vida continua mesmo depois de a alegria se perder, Jack e Diane estão “a fazer o melhor que podem” nos computadores (ainda “segurando” até 16′ – desculpem, estas são piadas de John Mellencamp que provavelmente não fazem sentido fora dos EUA). Agora a encriptação que está prestes a ter lugar é digital.

O computador de Jack utilizará a sua chave, que é realmente um algoritmo extremamente complicado que foi derivado de dados partilhados pelos dispositivos de Jack e Diane, para encriptar o texto em quadratura. Diane usa a sua chave simétrica correspondente para decifrar e ler os dados.

Mas o que é que está realmente a ser encriptado? Como se encripta “dados?”

No exemplo original havia letras reais num pedaço de papel físico que foram transformadas noutra coisa. Mas como é que um computador encripta dados?

Isso remonta à forma como os computadores lidam realmente com os dados. Os computadores armazenam informação em formato binário. 1’s e 0’s. Qualquer entrada de dados num computador é codificada para que seja legível pela máquina. São os dados codificados, na sua forma bruta, que são encriptados. Isto faz parte do que vai para os diferentes tipos de ficheiros utilizados pelos certificados SSL/TLS, depende parcialmente do tipo de esquema de codificação que se está a tentar encriptar.

Então o computador de Jack codifica os dados codificados e transmite para o computador de Diane, que utiliza a chave privada associada para decifrar e ler os dados.

Até agora, enquanto a chave privada permanecer, sabe… privada, a encriptação permanece segura.

A encriptação moderna resolveu o maior obstáculo histórico à encriptação: a troca de chaves. Historicamente, a chave privada tinha de ser fisicamente transmitida. A segurança da chave era literalmente uma questão de armazenar fisicamente a chave num local seguro. O compromisso da chave não só tornava a encriptação discutível, como podia fazer com que fosse morto.

Nos anos 70 um trio de criptógrafos, Ralph Merkle,Whitfield Diffie e Martin Hellman, começou a trabalhar numa forma de partilhar com segurança uma chave de encriptação numa rede insegura com um atacante a vigiar. Foram bem sucedidos a um nível teórico, mas não conseguiram encontrar uma função de encriptação assimétrica que fosse prática. Também não tinham qualquer mecanismo de autenticação (mas isso é uma conversa totalmente diferente). Merkle surgiu com o conceito inicial, mas o seu nome não está associado ao protocolo de troca chave que inventaram – apesar dos protestos dos seus outros dois criadores.

Sobre um ano mais tarde Ron Rivest, Adi Shamir e Leonard Adleman criaram um método de troca de chaves epónimo baseado na troca de chaves Diffie-Hellman (RSA), um método que também incluía funções de encriptação/desencriptação e autenticação. Isto é relevante porque foi o nascimento de toda uma nova iteração de encriptação: a encriptação assimétrica.

Deram-nos também o Bob e a Alice acima mencionados, o que para mim, pelo menos, faz com que seja uma espécie de lavagem.

Anyway, compreender a diferença entre a encriptação simétrica e assimétrica é fundamental para o resto desta discussão.

Asimetric Encryption vs. Symmetric Encryption

A encriptação assimétrica é por vezes chamada encriptação de chave privada, porque ambas as partes devem partilhar uma chave simétrica que pode ser usada tanto para encriptar como para desencriptar dados.

Criptografia simétrica, por outro lado, é por vezes chamada de encriptação de chave pública. Uma melhor maneira de pensar na encriptação assimétrica pode ser pensar nela como encriptação unidireccional.

Como ambas as partes partilham uma chave privada, existe um par de chaves. Uma parte possui uma chave pública que pode cifrar, a outra possui uma chave privada que pode decifrar.

A encriptação assimétrica é utilizada principalmente como mecanismo de troca de chaves privadas simétricas. Há uma razão para isto, a encriptação assimétrica é historicamente uma função mais cara devido ao tamanho das suas chaves. Assim, a criptografia de chave pública é mais utilizada como uma parede externa para ajudar a proteger as partes, uma vez que estas facilitam uma ligação, enquanto que a criptografia simétrica é utilizada dentro da própria ligação.

2048-bit keys vs. 256-bit keys

In SSL/TLS, a criptografia assimétrica serve uma função, extremamente importante. Permite ao cliente encriptar os dados que serão utilizados por ambas as partes para derivar as chaves de sessão simétricas que irão utilizar para comunicar. Nunca poderia usar a encriptação assimétrica para comunicar funcionalmente. Embora a chave pública possa ser utilizada para verificar uma assinatura digital, não pode descodificar nada que a chave privada encripte, por isso chamamos à encriptação assimétrica “uma via”.

Mas o maior problema é que o tamanho da chave torna as funções reais de encriptação e de desencriptação dispendiosas em termos dos recursos da CPU que devoram. É por isso que muitas organizações e empresas maiores, ao implantarem SSL/TLS em escala, descarregam os apertos de mão: para libertar recursos nos seus servidores de aplicação.

Em vez disso, utilizamos a encriptação simétrica para a comunicação real que ocorre durante uma ligação encriptada. Chaves simétricas aresmaller e menos dispendiosas para calcular.

Então, quando se vê alguém referenciar uma chave privada de 2048 bits, é muito provável que se esteja a referir a uma chave privada RSA. Isso é uma chave assimétrica. Precisa de ser suficientemente resistente a ataques, porque desempenha uma função tão crítica. Além disso, porque a troca de chaves é o melhor vector de ataque para comprometer uma ligação. É muito mais fácil roubar os dados utilizados para criar a chave de sessão simétrica e calculá-la você mesmo do que ter de rachar a chave pela força bruta depois de já estar em uso.

Isso levanta a questão: “Quão forte é a encriptação de 256 bits?” Se for menos robusta do que uma chave de 2048 bits, ainda é suficiente? E vamos responder a isso, mas primeiro precisamos de cobrir um pouco mais de terreno para fornecer o contexto correcto.

O que é exactamente um “bocadinho” de segurança?

É realmente importante que discutamos bits de segurança e comparando a força da encriptação entre algoritmos antes de entrarmos em qualquer discussão prática de quão forte é realmente 256 bits de segurança.Porque não é uma comparação 1:1.

Por exemplo, uma chave AES de 128 bits, que é metade do tamanho actualmente recomendado, é aproximadamente equivalente a uma chave RSA de 3072 bits em termos da segurança actualsecurity que fornecem.

É também importante compreender a diferença entre a reivindicação de segurança e o nível de segurança.

• Reclamação de Segurança – Este é o nível de segurança que a criptografia primitiva – a cifra ou função hash em questão – foi inicialmente concebida para atingir.
• Nível de Segurança – A força ACTUAL que a criptografia primitiva atinge.

Isto é tipicamente expresso em bits. Um bit é uma unidade básica de informação. É na realidade um portmanteau de “dígito binário”, que é incrivelmente eficiente e também não tão eficiente. Claro, é mais fácil de dizer bit. Mas acabei de passar um parágrafo inteiro a explicar que um bit é basicamente um 1 ou um 0 em binário, quando o termo original teria conseguido isso em duas palavras. Portanto, decide-se se é mais eficiente. De qualquer modo, não vamos gastar muito mais tempo em binário do que já temos, mas Ross escreveu um grande artigo sobre o assunto há alguns meses atrás, que deveria ser verificado.

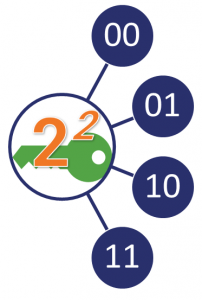
Anyway, o nível de segurança e a reclamação de segurança são tipicamente expressos em bits. Neste contexto, os bits de segurança, referimo-nos a isso como (n) refere-se ao número de operações que um atacante precisaria hipoteticamente de realizar para adivinhar o valor da chave privada. Quanto maior for a chave, mais difícil é adivinhar/cracar. Lembre-se, esta chave está em 1s e 0s, pelo que existem dois valores potenciais para cada bit. O atacante teria de realizar operações 2n para rachar a chave.

Isso pode ser um pouco abstracto demais, por isso aqui vai um exemplo rápido: Digamos que há uma chave de 2 bits. Isso significa que terá 22 (4) valores.

Isso seria trivialmente fácil para um computador de rachar, mas quando se começa a entrar em tamanhos de chave maiores, torna-se proibitivamente difícil para um computador moderno adivinhar correctamente o valor de uma chave privada em qualquer quantidade de tempo razoável.

Mas antes de chegarmos à matemática, voltemos à reclamação de segurança vs. nível de segurança

Reivindicação de segurança vs. nível de segurança

Tipicamente, quando se vê a encriptação comercializada, está-se a ver a Reclamação de Segurança a ser anunciada. É isso que o nível de segurança seria em condições óptimas. Vamos manter isto específico para SSL/TLS e PKI, mas a percentagem de tempo em que as condições óptimas estão presentes está longe de ser 100%. As configurações erradas são comuns, tal como é comum manter o suporte para versões mais antigas de SSL/TLS e conjuntos de cifras desactualizadas para fins de interoperabilidade.

No contexto do SSL/TLS, quando um cliente chega a um website, ocorre um aperto de mão em que as duas partes determinam um conjunto de cifras a utilizar de comum acordo. A força de encriptação que realmente se obtém depende dos parâmetros decididos durante o aperto de mão, bem como das capacidades do próprio servidor e do cliente.

Por vezes a encriptação de 256 bits fornece apenas um nível de segurança de 128 bits. Isto é particularmente comum com algoritmos de hashing, que medem a resistência a dois tipos diferentes de ataques:

• Colisões – Onde dois pedaços diferentes de dados produzem o mesmo valor de hash é chamado de colisão e quebra o algoritmo.
• resistência PreImage – Quão resistente e algoritmo é a uma exploração onde um atacante tenta encontrar uma mensagem com um valor de hash específico.

Assim, por exemplo, SHA-256 tem uma resistência à colisão de 128 bits (n/2) , mas uma resistência PreImage de 256 bits. Obviamente, o hashing é diferente da encriptação mas há também muitas semelhanças que fazem com que valha a pena mencioná-lo.

Então, quão forte é a encriptação de 256 bits?

Again, isto varia com base no algoritmo que está a utilizar, e varia da encriptação assimétrica à simétrica. Como dissemos, estas não são comparações 1:1. De facto, o nível de segurança da encriptação assimétrica não é realmente tão científico como poderia parecer. A encriptação assimétrica baseia-se em problemas matemáticos que são fáceis de executar de uma forma (encriptação) mas extremamente difíceis de reverter (decifragem). Devido a isso, os ataques contra a chave pública, os sistemas de criptografia assimétrica são tipicamente muito mais rápidos do que o estilo de força bruta procura o espaço da chave que atormenta a chave privada, esquemas de criptografia simétrica. Assim, quando se fala do nível de segurança da criptografia de chave pública, não se trata de uma figura definida, mas de um cálculo da dureza computacional da implementação contra o melhor e mais conhecido ataque actualmente.

Força de encriptação simétrica é um pouco mais fácil de calcular, devido à natureza dos ataques contra os quais têm de se defender.

Então, vejamos AES ou Advanced Encryption Standard, que é comummente utilizado como cifra em massa com SSL/TLS. As cifras a granel são os sistemas criptográficos simétricos que efectivamente tratam da segurança da comunicação que ocorre durante uma ligação HTTPS encriptada.

Existem historicamente dois sabores: cifras de bloco e cifras de fluxo.

Cifras de bloco quebram tudo o que encriptam em blocos de tamanho chave e encriptam-nos. A decifragem envolve a junção dos blocos. E se a mensagem for demasiado curta ou demasiado longa, o que é a maioria das vezes, têm de ser quebradas e/ou acolchoadas com dados descartáveis para que tenham o comprimento adequado. Os ataques de acolchoamento são uma das ameaças mais comuns ao SSL/TLS.

TLS 1.3 eliminou este estilo de encriptação em massa exactamente por essa razão, agora todas as cifras devem ser definidas para o modo stream. As cifras de fluxo encriptam dados em fluxos pseudo-aleatórios de qualquer comprimento, são consideradas mais fáceis de implementar e requerem menos recursos. O TLS 1.3 também eliminou algumas cifras de fluxo inseguras, como a RC4, também.

Então, resumindo, existem realmente apenas dois bulkciphers sugeridos hoje em dia, AES e ChaCha20. Vamos agora concentrar-nos nas AES, porque ChaCha20 é um animal diferente.

GCM significa Galois Counter Mode, que permite que AES – que na realidade é uma cifra de bloco – funcione em modo de fluxo. O CCM é semelhante, penteando um modo contador com funções de autenticação de mensagem.

Como cobrimos, pode realmente executar AES em segurança em GCM ou CCM com chaves de 128 bits e ficar bem. Está a obter o equivalente a 3072-bit RSA em termos do nível de segurança. Mas tipicamente sugerimos que utilize chaves de 256-bit para que mantenha a dureza computacional máxima durante o maior período de tempo.

Então, vejamos essas chaves de 256-bit. Uma chave de 256 bits pode ter2256 combinações possíveis. Como mencionámos anteriormente, uma chave de dois bits teria quatro combinações possíveis (e seria facilmente rachável por um dois bitscrook). No entanto, estamos aqui a lidar com exponenciação, por isso cada vez que se aumenta a exponencialidade, n, aumenta-se o número de combinações possíveis de forma selvagem. 2256 é 2 x 2, x 2, x 2, x 2… 256 vezes.

Como já abordámos, a melhor maneira de decifrar uma chave de encriptação é ‘brute-forcing’, que é basicamente apenas uma tentativa & erro em termos simples. Assim, se o comprimento da chave é 256-bit, haveria 2256 combinações possíveis, e um hacker deve tentar a maioria das 2256 combinações possíveis antes de chegar à conclusão. Provavelmente não será preciso tentar todas elas para adivinhar a chave – normalmente é cerca de 50% – mas o tempo necessário para o fazer duraria muito para além de qualquer tempo de vida humana.

Uma chave privada de 256 bits terá 115.792.089.237.316.195.423.570.985.008.687.907.853.269.
984.665.640.564.039.457.584.007.913.129.639.936 (ou seja, 78 dígitos) combinações possíveis. Nenhum Super Computador na face desta terra pode rachar isso em qualquer período de tempo razoável.

Even se usar Tianhe-2 (MilkyWay-2), o supercomputador mais rápido do mundo, levará milhões de anos a rachar a encriptação AES de 256-bit.

Esse número de rochas celestes ainda mais quando se tenta descobrir o tempo que levaria a factor uma chave privada RSA. Uma chave RSA de 2048 bits levaria 6,4 quadriliões de anos (6.400.000.000.000.000 anos) a calcular, por DigiCert.

Ninguém tem esse tipo de tempo.

Computação quântica vai mudar tudo isto

Agora seria um bom ponto para falar um pouco sobre encriptação quântica e a ameaça que ela representa para os nossos primitivos criptográficos modernos. Como acabámos de cobrir, os computadores trabalham em binário. 1’s e 0’s. E a forma como os bits funcionam nos computadores modernos é que têm de ser um valor conhecido, ou são um 1 ou um 0. Isso significa que um computador moderno só pode adivinhar uma vez de cada vez.

Obviamente, isso limita severamente a rapidez com que consegue fazer combinações bruteforce num esforço para rachar uma chave privada.

Quantum Computers não terá tais limitações. Agora, duas coisas, antes de mais, a computação quântica ainda está a cerca de 7-10 anos de viabilidade, por isso ainda estamos longe de o conseguir. Alguns CAs, como DigiCert, começaram a colocar certificados digitais pós-quantum em dispositivos IoT que terão uma longa vida útil para tentar protegê-los preventivamente contra a computação quântica, mas para além disso, ainda estamos na fase de investigação quando se trata de encriptação à prova de quantum.

A questão é que os computadores quânticos não usam bits, eles usam bits quânticos ou qubits. Um bit quântico pode ser AMBOS um 1 e um 0 graças a um princípio chamado superposição, que é um pouco mais complicado do que o que vamos ter hoje. Os Qubits dão aos computadores quânticos o poder de exponenciar os seus ataques de força bruta, o que efectivamente anula a dureza computacional proporcionada pela exponenciação que teve lugar com a criptografia primitiva. Um computador Qubit quatro pode efectivamente estar em quatro posições diferentes (22) ao mesmo tempo. É mais uma vez 2n, pelo que um computador Quantum com n qubits pode tentar 2n combinações em simultâneo. Bristlecone, que tem 72 qubits, pode tentar 272 (4,722,366,482,869,645,213,696) valores de uma só vez.

Again, ainda estamos longe disso e o computador quântico teria de descobrir como executar com sucesso o algoritmo de Shor, outro tópico para outro dia, pelo que isto ainda é largamente teórico.

Parar, de repente 4,6 quadriliões de anos não parece ser tão longo.

Vamos embrulhar isto…

256 bits de encriptação é bastante padrão em 2019, mas a referência à encriptação de 256 bits não se refere à mesma coisa. Por vezes256-bits de encriptação apenas sobe para um nível de segurança de 128 bits. Por vezes, o tamanho da chave e o nível de segurança estão intrinsecamente ligados, enquanto outras vezes uma é apenas utilizada para se aproximar da outra.

Então, a resposta a “quão forte é a encriptação de 256 bits” não é uma resposta com um corte claro. Pelo menos não o tempo todo.

No contexto da encriptação SSL/TLS, porém, refere-se mais frequentemente à encriptaçãooAES, onde 256 bits significa realmente 256 bits. E, pelo menos por enquanto, que a encriptação de 256 bits ainda é bastante forte.

Quando um atacante que usa um computador moderno for capaz de capturar uma chave simétrica de 256 bits, não só terá sido descartada, como também terá provavelmente substituído o certificado SSL/TLS que ajudou a gerá-la.

Em suma, a maior ameaça à sua encriptação e às suas chaves de encriptação continua a ser a má gestão, a tecnologia por detrás delas é sólida.