As origens da geometria
As primeiras linhas que os homens alguma vez imaginaram eram linhas rectas e círculos. Estas marcaram o nascimento da geometria, o que significa literalmente “Medição da Terra”, dando-nos uma ideia precisa do significado destas linhas. Os primeiros especialistas em geometria foram os geómetras no Antigo Egipto. Os gregos chamam-lhes “arpedonapti” – aqueles que fazem o nó das cordas. Os peritos egípcios costumavam apertar as cordas na terra para marcar linhas e círculos. Vestígios desta antiga utilização ainda estão presentes em muitas línguas modernas como, por exemplo, no ditado “desenhar uma linha”. O emprego de cordas para as operações de medição da terra permaneceu inalterado durante vários séculos e ainda pode ser encontrado no trabalho de topógrafos terrestres em tempos relativamente recentes.
Os historiadores gregos testemunham o nascimento da geometria (literalmente:Medição da Terra)no Egipto. Heródoto diz:
Se o rio tivesse simplesmente cancelado as fronteiras do pedaço de terra, era papel dos funcionários redesenhar as divisões exactas.
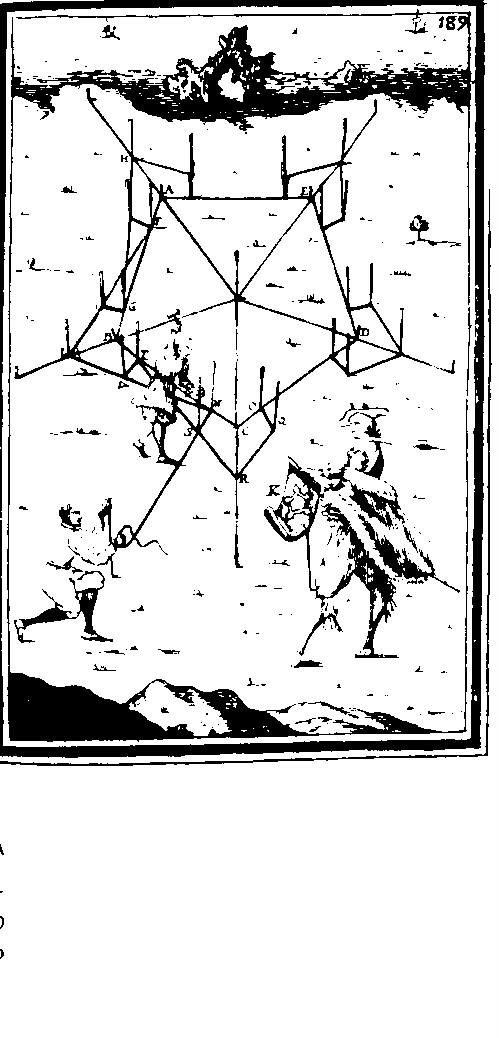 os especialistas em geometria egípcia eram chamados de “arpedonapti”, aqueles que davam nós às cordas. Foi apertando as cordas que desenharam as duas linhas mais simples e mais importantes da geometria: a linha recta e o círculo. A primeira, simplesmente apertando uma corda entre dois pontos, um tipo de operação cuja imagem ainda está presente nas expressões “desenhar em linha”, “desenhar uma perpendicular”; a segunda, fazendo girar um dos dois pontos em torno do outro que é mantido fixo. Poderiam eles imaginar a extensão do desenvolvimento destas duas práticas elementares? Muito provavelmente não. De facto, as necessidades práticas dos antigos medidores da terra, supostamente em breve, fizeram surgir a necessidade de obras do tipo que hoje chamamos “com quadrado e bússola” e que deveriam chamar-se mais propriamente “com círculos e linhas rectas”.
os especialistas em geometria egípcia eram chamados de “arpedonapti”, aqueles que davam nós às cordas. Foi apertando as cordas que desenharam as duas linhas mais simples e mais importantes da geometria: a linha recta e o círculo. A primeira, simplesmente apertando uma corda entre dois pontos, um tipo de operação cuja imagem ainda está presente nas expressões “desenhar em linha”, “desenhar uma perpendicular”; a segunda, fazendo girar um dos dois pontos em torno do outro que é mantido fixo. Poderiam eles imaginar a extensão do desenvolvimento destas duas práticas elementares? Muito provavelmente não. De facto, as necessidades práticas dos antigos medidores da terra, supostamente em breve, fizeram surgir a necessidade de obras do tipo que hoje chamamos “com quadrado e bússola” e que deveriam chamar-se mais propriamente “com círculos e linhas rectas”.
Hoje em dia, é tão natural considerar o papel na arena natural da geometria, de modo que concebemos o uso apenas de quadrados e bússolas, como um limite arbitrário introduzido por especulativospíritas que preferiam alguns números de axiomas ao múltiplo conforto da multiplicidade de instrumentos. Consequentemente, a diferença entre o perito em geometria teórica – estou naturalmente a referir-me ao clássico, Euclidiano e ao técnico – aquele que toma medidas, o arquitecto – reside principalmente no facto de o primeiro decidir, voluntariamente, não utilizar instrumentos, quadrados e pantógrafos, que o segundo utiliza em seu proveito.
Desta forma, tendemos a ignorar completamente a geometria “no campo” a favor daquela “no papel”, esta falhada torre reconhece que quando transferimos operações geométricas do campo para o papel, elas irão por vezes exigir técnicas e métodos totalmente diferentes.
Não se deve ignorar o facto de que a precisão de um plano é muito mais necessária no campo (àquele que mede e divide em partes um terreno, bem como ao arquitecto que faz com que os edifícios – na maioria das vezes estes dois sejam a mesma pessoa-) em vez de no papel. O arquitecto que tem uma ideia clara do plano global e que se lembra do processo que seguiu para o conseguir, precisaria de um esboço. Mapas relativamente recentes, bem como mapas antigos que foram, inevitavelmente, desenhados com instrumentos e suporteshrudimentary, não reproduzem exactamente os limites de um pedaço de terra. De facto, isto é impossível porque mesmo um erro de um ponto percentual – o mínimo que poderia ocorrer numa escala razoavelmente grande – daria origem a um absolutemismo que dificilmente poderia ser aceite no terreno. Neste caso, o conhecimento da forma e das medidas do objecto que está a ser descrito (um campo, um edifício), são fundamentais; será mais do que até ao especialista em geometria reproduzir no campo a precisão que falta no papel. O mesmo acontece com o matemático a quem a precisão dos números não é de modo algum útil nas demonstrações. A geometria no papel substitui a precisão das operações no campo, com a geometria do processo mental.
Pelo contrário, da lógica à exactidão material, como consequência do necessário alargamento da escala para passar do plano à sua criação efectiva, a acção de apertar uma corda tem permanecido uma das principais operações desde o Antigo Egipto e a Antiga Grécia. Esta prática permaneceu inalterada até aos tempos modernos, passando apenas pela invenção e aperfeiçoamento de certos instrumentos ópticos. Embora, no papel, seja fácil desenhar uma perpendicular por meio de réguas e quadrados, a mesma operação no campo, com o mesmo grau de precisão, exige métodos radicalmente diferentes. No campo, o quadrado é inútil porque é demasiado pequeno em relação às dimensões das formas. Mesmo que o quadrado seja extremamente preciso, a perpendicular que pode desenhar atingirá no máximo um metro. Se tivermos de marcar um quadrado de 30 metros por lado, temos de prolongar esta linha 30 vezes. Esta seria uma operação tão inexacta que provavelmente resultaria em resultados semelhantes, como se medíssemos o ângulo recto aproximadamente.
Estas reflexões remetem-nos para a questão inicial: que técnicas foram utilizadas pelos medidores egípcios para desenhar um pedaço de terra quadrado? Como obtiveram o ângulo quadrático?
Como alguns estudiosos sugeriram, é possível que tivessem o conhecimento do teorema de Pitágoras (século VI a.C.) ou, mais precisamente, a consciência do seu contrário, ou seja, o facto de um triângulo com lados de 3, 4 e 5, em que o quadrado do lado mais longo é igual à soma dos quadrados dos outros dois lados, ser um triângulo em ângulo recto. Portanto, se esticarmos uma corda de anel com um comprimento de 12 unidades, marcado em três pontos a uma distância de 3, 4 e 5, em direcção à forma de um triângulo com o vértice nos pontos marcados, o ângulo entre os lados mais curtos do triângulo é um ângulo recto.
Não se sabe se este era o processo que os antigos topógrafos terrestres utilizavam no seu tempo, pois não foi provado que os antigos egípcios sabiam que o triângulo com os lados 3, 4 e 5 é um triângulo em ângulo recto. Mesmo que estivessem conscientes disto, ou de outros triângulos pitagóricos (como é fortemente sugerido pela presença de vários trios pitagóricos, se não na matemática egípcia, então na babilónia), isto implica,necessariamente, que conheciam a natureza de, ou pelo menos como tocar o ângulo recto.
De onde veio este conhecimento? Devido à falta de documentação mesmo parcial e de testemunhas, podemos tentar abordar o problema a partir de uma pointofview diferente, uma matemática e não uma histórica. A questão que se coloca é o que torna um ângulo correcto diferente dos outros?ou melhor, que é a peculiaridade do ângulo do triângulo com os lados 3, 4 e 5?
A resposta imediata é: ao contrário de outros triângulos, os pitagóricos e mais particularmente os mais simples deles, o dos lados 3, 4 e 5, podem ser feitos para se poderem virar juntos de um lado e depois novamente do outro. Deste modo, obtém-se uma configuração simétrica que preenche totalmente todo o espaço disponível sem sobreposições ou lacunas.
 Nenhum outro ângulo a não ser o direito tem esta característica simétrica que obtém a sua própria definição no primeiro livro completo de geometria do nosso tempo, Elementos de Euclides (século IV a.C.):
Nenhum outro ângulo a não ser o direito tem esta característica simétrica que obtém a sua própria definição no primeiro livro completo de geometria do nosso tempo, Elementos de Euclides (século IV a.C.):
Quando uma linha recta que cai sobre outra forma ângulos iguais, estes são ambos rectos.
A natureza do ângulo quadrado reside no facto de que os ângulos resultantes da intersecção de duas linhas rectas são iguais. Isto pode ser imediatamente demonstrado no papel, dobrando o papel ao longo de uma das linhas convergentes e verificando que a outra linha se dobra sobre si mesma.
A construção geométrica “clássica” que consiste em marcar dois círculos e depois unificar as suas intersecções também possui esta propriedade. O carácter simétrico da forma é bastante evidente, e é claramente à prova da igualdade dos ângulos. Além disso, ao contrário do pitagoreantriângulo que necessita de uma construção adicional, neste caso a forma sugere imediatamente a definição de ângulo quadrado através da igualdade dos ângulos e, ao mesmo tempo, constrói-se a si própria.
Estas são ainda suposições simples. Sem qualquer dúvida, este processo é definitivamente mais simples e de maior precisão do que o primeiro. Onecsaysay desta forma só podemos marcar a perpendicular que passa pelo centro do segmento dado, também chamado o eixo do segmento. No entanto, não é difícil notar que, se precisarmos de uma aperpendicular num extremo, como no caso do desenho de um quadrado, será necessário duplicar o segmento que o prolonga para onde se quer desenhar a perpendicular e depois repetir o processo anterior.É necessário observar que todas estas técnicas são particularmente adequadas para terrenos planos como a planície egípcia.