Matemática | Média, Variância e Desvio Padrão

Média é a média de um dado conjunto de dados. Consideremos abaixo o exemplo

p> Estes oito pontos de dados têm a média (média) de 5:

$\frac{2 + 4 + 4 + 4 + 4 + 5 + 5 + 7 + 9}{8} = 5.$

$Formula : \mu=\frac{\sum_{i=1}^{N} x_{i}{N}$

onde μ é a média e x1, x2, x3…., xi são elementos.Note também que a média é por vezes denotada por $\bar{x}$

br>>Variância é a soma dos quadrados de diferenças entre todos os números e meios.
Deviação por exemplo acima. Primeiro, calcular os desvios de cada ponto de dados a partir da média, e ajustar o resultado de cada:

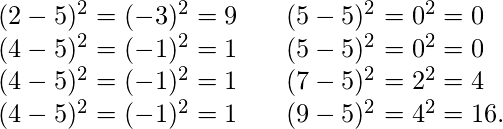
$\begin{array}{lll} (2-5)^2 = (-3)^2 = 9 (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 (5-5)^2 = 0^2 = 0 \\ (4-5)^2 = (-1)^2 = 1 (7-5)^2 = 2^2 = 4 \\ (4-5)^2 = (-1)^2 = 1 (9-5)^2 = 4^2 = 16. \\ Fim de discussão$

variância = $\frac{9 + 1 + 1 + 1 + 0 + 0 + 4 + 16}{8}$ = 4.

$Formula: \sigma^{2}= \frac {\i=1}^{N} (x_{i}-{2}}{N}}{N$

Onde μ é Média, N é o número total de elementos ou frequência de distribuição.

Desvio Padrão é a raiz quadrada da variância. É uma medida da medida em que os dados variam em relação à média.

Desvio Padrão (para dados acima) = $\sqrt{ 4 }$ = 2

Porque é que os matemáticos escolheram um quadrado e depois uma raiz quadrada para encontrar o desvio, porque não tomar simplesmente a diferença de valores?
Uma razão é que a soma das diferenças se torna 0 de acordo com a definição de média. A soma das diferenças absolutas poderia ser uma opção, mas com diferenças absolutas, era difícil provar muitos teoremas simpáticos.

$\textup{Coeficiente de variação } =\frac{ \textup{Desvio padrão}}{Mean}*100$

Valor do desvio padrão é 0 se todas as entradas no input forem iguais.
Se adicionarmos (ou subtrairmos) um número digamos 7 a todos os valores do conjunto de input, a média é aumentada (ou diminuída) em 7, mas o desvio padrão não muda.Se multiplicarmos todos os valores do input definido por um número 7, tanto a média como o desvio padrão são multiplicados por 7. Mas se multiplicarmos todos os valores de input com um número negativo digamos -7, a média é multiplicada por -7, mas o desvio padrão é multiplicado por 7,
Desvio padrão e a variância é uma medida que diz como os números estão espalhados. Enquanto a variância lhe dá uma ideia aproximada da dispersão, o desvio padrão é mais concreto, dando-lhe distâncias exactas da média.
Medida, mediana e modo são a medida da tendência central dos dados (agrupados ou não agrupados).

Perguntas baixas foram feitas nos exames do ano anterior GATE
http://quiz.geeksforgeeks.org/gate-gate-cs-2012-question-64/

GeeksforGeeks

Deixe uma resposta Cancelar resposta