Uma correlação ou simples análise de regressão linear pode determinar se duas variáveis numéricas estão significativamente relacionadas de forma linear. Uma análise de correlação fornece informação sobre a força e direcção da relação linear entre duas variáveis, enquanto uma análise de regressão linear simples estima parâmetros numa equação linear que podem ser utilizados para prever valores de uma variável com base na outra.
Correlação
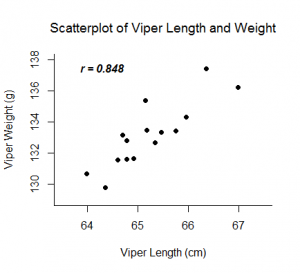
O coeficiente de correlação de Pearson, r, pode assumir valores entre -1 e 1. Quanto mais distante r estiver de zero, mais forte será a relação linear entre as duas variáveis. O sinal de r corresponde à direcção da relação. Se r é positivo, então à medida que uma variável aumenta, a outra tende a aumentar. Se r é negativo, então à medida que uma variável aumenta, a outra tende a diminuir. Uma relação linear perfeita (r=-1 ou r=1) significa que uma das variáveis pode ser perfeitamente explicada por uma função linear da outra.
Exemplos:

Regressão linear
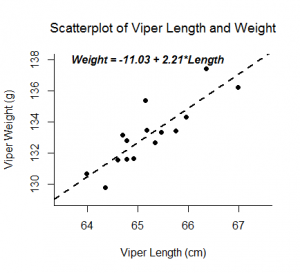
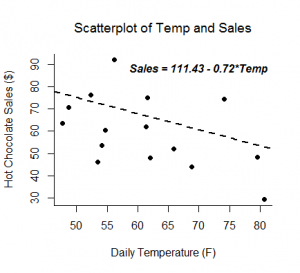
Uma análise de regressão linear produz estimativas para a inclinação e intercepção da equação linear que prevê uma variável de resultado, Y, baseada em valores de uma variável de previsão, X. Uma forma geral desta equação é mostrada abaixo:
![]()
A intercepção, b0, é o valor previsto de Y quando X=0. A inclinação, b1, é a mudança média em Y para cada aumento de uma unidade em X. Além de lhe dar a força e a direcção da relação linear entre X e Y, a estimativa da inclinação permite uma interpretação de como Y muda quando X aumenta. Esta equação também pode ser usada para prever valores de Y para um valor de X.
Exemplos:
Inferência
Testes de inclinação podem ser executados tanto na correlação como nas estimativas de inclinação calculadas a partir de uma amostra aleatória de uma população. Ambas as análises são testes t executados na hipótese nula de que as duas variáveis não estão linearmente relacionadas. Se forem executados com os mesmos dados, um teste de correlação e um teste de inclinação fornecem a mesma estatística de teste e o mesmo valor p.
Assumptions:
- Amostras aleatórias
- Observações independentes
- A variável de previsão e a variável de resultado estão relacionadas linearmente (avaliadas através da verificação visual de um gráfico de dispersão).
- A população de valores para o resultado são normalmente distribuídos para cada valor do preditor (avaliado pela confirmação da normalidade dos resíduos).
- A variância da distribuição do resultado é a mesma para todos os valores do preditor (avaliado pela verificação visual de um gráfico residual para um padrão de funilagem).
Hipóteses:
Ho: As duas variáveis não estão linearmente relacionadas.
Ha: As duas variáveis estão relacionadas de forma linear.
Equações Relevantes:
Graus de liberdade: df = n-2

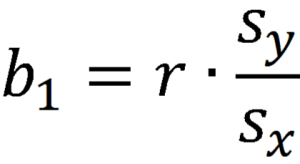
![]()
Exemplo 1: Cálculo manual
Estes vídeos investigam a relação linear entre as alturas das pessoas e as medidas do vão do braço.
Correlação:


Regressão:


Amostra de conclusão: Investigando a relação entre o vão do braço e a altura, encontramos uma grande correlação positiva (r=.95), indicando uma forte relação linear positiva entre as duas variáveis. Calculámos a equação para a linha de melhor ajuste como Armspan=-1,27+1,01(Altura). Isto indica que para uma pessoa que tenha zero polegadas de altura, a sua envergadura de braço prevista seria de -1,27 polegadas. Isto não é um valor possível, uma vez que o alcance dos nossos dados cairá muito mais alto. Para cada aumento de 1 polegada de altura, prevê-se que a envergadura do braço aumente 1,01 polegadas.
Exemplo 2: Realizar análise em Excel 2016
Algumas destas análises requerem que tenha o add-in Data Analysis ToolPak em Excel activado. Para instruções sobre a realização desta análise em versões anteriores do Excel, visite https://stat.utexas.edu/videos
Dataset usado em vídeos
Matriz de correlação e p-valor:
Direcções PDF correspondentes ao vídeo

Criar scatterplots:
Direcções PDF correspondentes ao vídeo
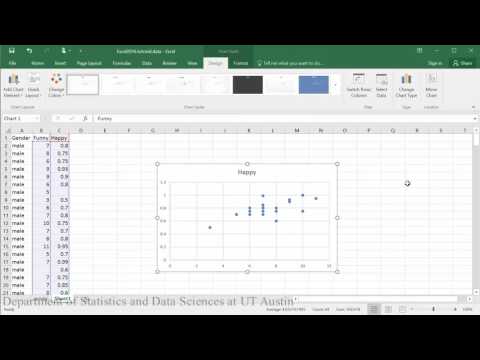

Modelo linear (primeira metade do tutorial):
Direcções PDF correspondentes ao vídeo
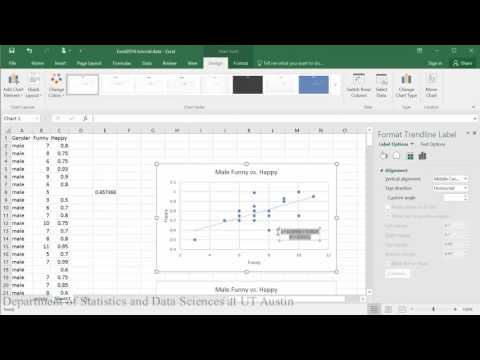

Criar parcelas residuais:
Direcções PDF correspondentes ao vídeo

>p>Conclusão da amostra: Ao avaliar a relação entre o quão feliz alguém está e o quão engraçado outros os classificaram, o gráfico de dispersão indica que parece existir uma relação linear positiva moderadamente forte entre as duas variáveis, que é suportada pelo coeficiente de correlação (r = .65). Uma verificação das hipóteses utilizando o gráfico residual não indicou quaisquer problemas com os dados. A equação linear para prever feliz de engraçado foi Happy=.04+0.46(Funny). A equação y indica que, para uma pessoa cuja classificação da piada era zero, a sua felicidade está prevista em .04. A classificação engraçada prevê significativamente a felicidade de tal forma que para cada 1 ponto de aumento na classificação engraçada, prevê-se que os homens aumentem .46 na felicidade (t = 3,70, p = .002).
Exemplo 3: Realização de análise em R
Os vídeos seguintes investigam a relação entre o IMC e a pressão arterial para uma amostra de pacientes médicos.
Dataset usado em vídeos
Correlação:
R ficheiro de script usado em vídeo
/p>

/div>
Regressão:
R ficheiro de script usado em vídeo