A Ordem de Operações: PEMDAS

Parece que a resposta depende da forma como se olha para o problema. Mas não podemos ter este tipo de flexibilidade em matemática; a matemática não funcionará se não se puder ter a certeza da resposta, ou se a mesma expressão puder ser calculada de modo a que se possa chegar a duas ou mais respostas diferentes.

Para eliminar esta confusão, temos algumas regras de precedência, estabelecidas pelo menos desde os anos 1500, chamadas de “ordem de operações”. As “operações” são adição, subtracção, multiplicação, divisão, exponenciação e agrupamento; a “ordem” destas operações indica quais as operações que têm precedência (são tratadas) perante as quais outras operações.

Uma técnica comum para recordar a ordem das operações é a abreviatura (ou, mais propriamente, a “sigla”) “PEMDAS”, que se transforma na frase mnemónica “Por favor desculpe a minha querida tia Sally”. Esta frase representa, e ajuda a lembrar a ordem de “Parênteses, Expoentes, Multiplicação e Divisão, e Adição e Subtracção”. Esta listagem diz-lhe as classificações das operações: Os parênteses superam os expoentes, que superam a multiplicação e divisão (mas a multiplicação e divisão estão na mesma ordem), e a multiplicação e divisão superam a adição e subtracção (que estão juntas na ordem inferior). Por outras palavras, a precedência é:

Quando se tem um monte de operações da mesma ordem, opera-se apenas da esquerda para a direita. Por exemplo, 15 ÷ 3 × 4 não é 15 ÷ (3 × 4) = 15 ÷ 12, mas é antes (15 ÷ 3) × 4 = 5 × 4, porque, indo da esquerda para a direita, chega-se primeiro ao sinal de divisão.

Se não tiver a certeza disto, teste-o na sua calculadora, que foi programada com a hierarquia de Ordem de Operações. Por exemplo, escrevendo a expressão acima numa calculadora gráfica, obterá:

(Nota: Os falantes de inglês britânico utilizam frequentemente a sigla “BODMAS”, em vez de “PEMDAS”. BODMAS significa “Brackets, Orders, Division and Multiplication, and Addition and Subtraction” (Parênteses, Encomendas, Divisão e Multiplicação, e Adição e Subtracção). Uma vez que “parênteses” são os mesmos que parênteses e “ordens” são os mesmos que expoentes, os dois acrónimos significam a mesma coisa. Também se pode ver que o “M” e o “D” estão invertidos na versão Inglesa-Britânica; isto confirma que a multiplicação e a divisão estão na mesma “classificação” ou “nível”. Os canadianos de língua inglesa dividem a diferença, usando BEDMAS.)

A ordem das operações foi estabelecida de modo a evitar erros de comunicação, mas PEMDAS pode gerar a sua própria confusão; alguns estudantes por vezes tendem a aplicar a hierarquia como se todas as operações de um problema estivessem no mesmo “nível” (indo simplesmente da esquerda para a direita), mas muitas vezes essas operações não são “iguais”. Muitas vezes ajuda a trabalhar problemas de dentro para fora, em vez de da esquerda para a direita, porque muitas vezes algumas partes do problema estão “mais para baixo” do que outras partes. A melhor maneira de explicar isto é fazer alguns exemplos:

• Simplificar 4 + 32.

• Simplificar 4 + (2 + 1)2.

• Simplificar 4 + 2.

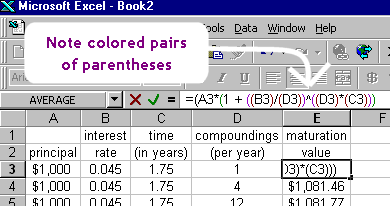
Não há um significado particular na utilização de parênteses rectos (o “” acima) em vez de parênteses. Os parênteses e as frisos (os caracteres “{” e “}”) são utilizados quando existem parênteses aninhados, como uma ajuda para saber quais os parênteses que vão com qual parênteses. Os diferentes caracteres de agrupamento são utilizados apenas por conveniência. Isto é semelhante ao que acontece numa folha de cálculo Excel quando se introduz uma fórmula usando parênteses: cada conjunto de parênteses é codificado por cores, para que se possa distinguir os pares:

• Simplificar

Então a minha resposta simplificada é

A página seguinte tem mais exemplos trabalhados….