4.2: Momento Magnético e Torque

Momento Dipolo Magnético

Aqui introduzimos um atalho para cálculos futuros de torque. A quantidade é a área do laço, (yz). Em aplicações futuras, podemos ter a corrente alimentada no laço por um único fio, que é enrolado em torno do perímetro várias vezes. A força exercida em cada lado do laço (e portanto o torque) será então multiplicada pelo número de voltas no fio, (N). O produto de N, I e A é escrito como uma única quantidade, dando a magnitude do binário para este caso a forma simples de B. Se este laço gira sobre o seu eixo, então o braço do momento encolhe. Por exemplo, se o topo do laço rodar para trás e o fundo rodar para a frente por { 90^o}, então as forças sobre esses segmentos estarão directamente afastadas umas das outras. Estas forças actuam directamente através do eixo, pelo que o binário que produzem é zero. Sabemos que o torque e o campo magnético são ambos vectores, e o torque criado está relacionado com a orientação do laço no campo. Podemos contabilizar a orientação do laço definindo um momento dipolo magnético:

\

O vector \(\ sobre-linha direita A\) tem uma magnitude igual à área do laço, e tem uma direcção que é perpendicular ao plano do laço, na direcção definida como se segue: Curva os dedos da mão direita numa direcção que traça a direcção da corrente em torno do laço, e o polegar dessa mão aponta a direcção do vector. Por exemplo, o laço na Figura 4.2.1 teria um momento magnético que aponta para fora da página.

O vector de torque pode agora ser calculado a partir do momento dipolo magnético da mesma forma que o torque exercido sobre um dipolo eléctrico foi calculado:

\

Podemos ver que isto funciona para o caso mostrado na Figura 4.2.1: O ângulo entre o momento dipolo magnético (que aponta para fora da página) e o campo magnético é \(90^o), pelo que o seno do ângulo entre estes vectores que aparece no produto cruzado é 1, dando a resposta que encontramos acima. Quando o laço gira em torno do eixo horizontal, o ângulo entre o momento dipolo magnético e o campo muda, reduzindo os braços do momento das forças por um factor de (seno) – exactamente a quantidade contabilizada no produto cruzado. Quando o laço roda até ao ponto em que o seu plano é perpendicular ao campo, o momento magnético e o campo são paralelos, fazendo com que o binário seja zero, como encontramos acima.

P>Embora tenhamos derivado a fórmula para o momento dipolo magnético usando um rectângulo, verifica-se que enquanto o laço estiver num plano, a fórmula funciona independentemente da sua forma. Como exemplo ilustrativo, vamos resolver o torque num laço circular. Este é um exemplo mais difícil do que o rectângulo, por razões que se tornarão claras, mas demonstra ferramentas importantes para integrar contribuições infinitesimais e lidar com produtos vectoriais.

Figure 4.2.2a – Torque num Laço Circular Fechado de Fio num Campo Magnético Uniforme

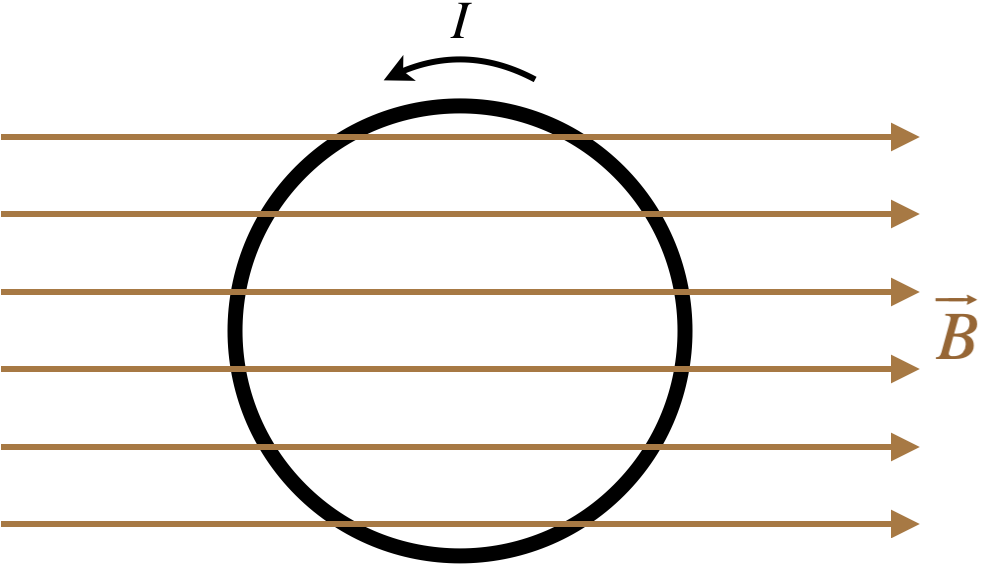
Tal como fizemos para integrar distribuições de carga para obter campos, começamos por introduzir um sistema de coordenadas (certifique-se de que é destra, i.e. escolher os eixos de modo a que \\\i1), seleccionar uma peça infinitesimal do laço, e descrevê-la em termos de coordenadas, etiquetando as variáveis que precisaremos de conhecer ao longo do percurso.

Figure 4.2.2b – Torque num loop circular fechado de fio num campo magnético uniforme

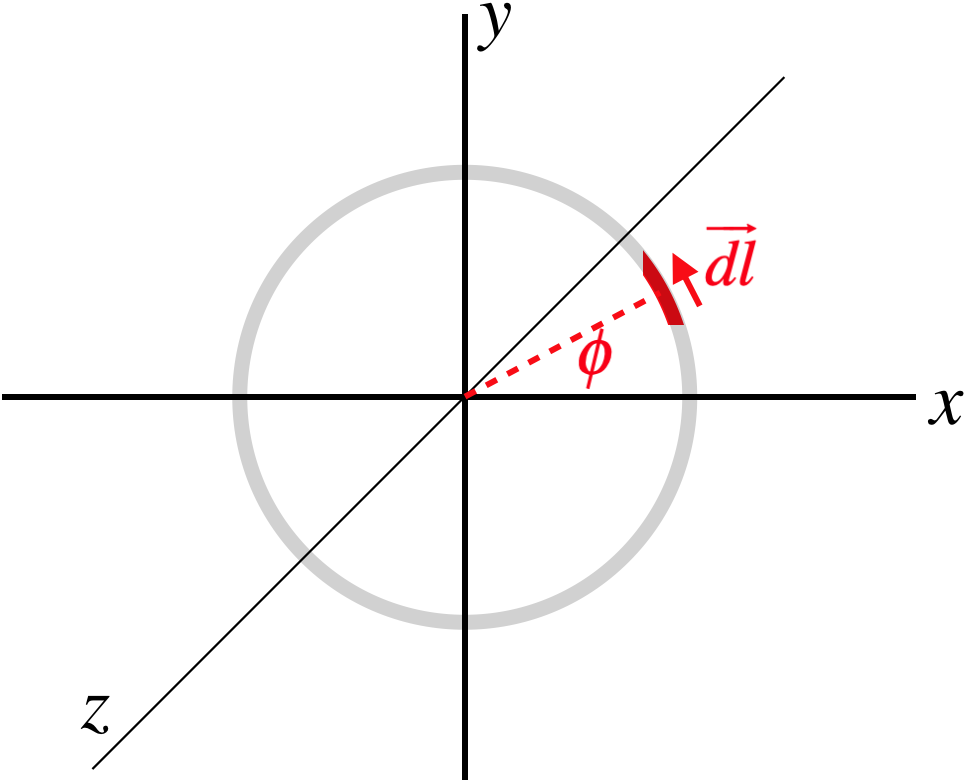p>>P>Aqui escolhemos colocar o loop no plano \(x\)-(y), e o campo magnético aponta na direcção \(+x)-direcção. Uma fatia infinitesimal de arame foi seleccionada num ângulo superior do eixo.

p>P>P>A seguir precisamos de expressar matematicamente o vector. A sua magnitude é o comprimento de um segmento infinitesimal de arco, que é o Rphi (R;dphi). A direcção é mais complicada, mas explodindo a imagem e fazendo um pouco de geometria, podemos determinar os seus componentes:

Figure 4.2.3 – Escrevendo o Vector do Elemento Actual

P>Conjuntando-o num único vector:

p>>p> Agora temos tudo o que precisamos. Por mais complicada que seja a geometria com a força e depois o torque, não temos de a seguir – tudo o que precisamos de fazer é fazer correctamente a matemática vectorial. Por exemplo, a força sobre o elemento de corrente é:

vezes à esquerda]

p>Reciclando os produtos cruzados dos vectores de unidade de Física 9A, ligamos {widehat i = 0} e {widehat j = -widehat k), e a força sobre este elemento torna-se:

\\

Para obter o binário, escolhemos a origem como ponto de referência, e calculamos directamente a contribuição infinitesimal para o binário. Ligando o vector de posição e fazendo as contas vectoriais:

\\]

Tudo o que resta é somar todas as contribuições de torque, o que significa integrar sobre o ângulo {\phi} a partir do ângulo de 2pi{\phi}:

P> P> = IR^2B=I^2B esquerda=I^2B direita)B>;|widehat j>]p>Suramente, a magnitude do binário revela-se, onde E utilizando a regra da direita para obter a direcção do momento magnético (fora da página), seguida da direcção do binário da regra da direita aplicada à seta de direita-acima da seta de direita-acima da seta de direita-baixo, confirma que a direcção também funciona.

Este problema pareceu muito assustador porque a direcção da seta para a direita está a mudar em todo o círculo, mas uma vez que este vector é escrito em termos de