Podemos agora analisar problemas nos quais tanto a condução como a convecção ocorrem, começando com uma parede arrefecida por fluido fluente em cada lado. Asdiscussed, uma descrição da transferência de calor por convecção pode ser dada explicitamente como
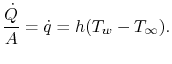
Isto pode representar um modelo de lâmina de turbina com arrefecimento interno. A figura 17.6 mostra a configuração.
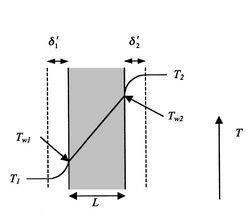 >br>
>br>A transferência de calor no fluido 1 é dada por
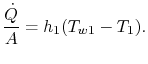
que é a transferência de calor por unidade de área para o fluido. A transferência de calor no fluido 2 é dada de forma semelhante por
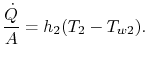
Do outro lado da parede, temos
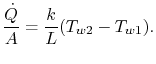
A quantidade ![]() é a mesma em todas estas expressões. Juntando-as todas para escrever a conhecida queda de temperatura global produz uma relação entre transferência de calor e queda de temperatura global,
é a mesma em todas estas expressões. Juntando-as todas para escrever a conhecida queda de temperatura global produz uma relação entre transferência de calor e queda de temperatura global, ![]() :
:
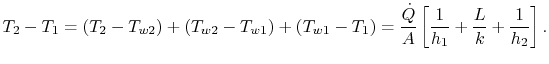 |
(17.20) |
Podemos definir uma resistência térmica, ![]() , como antes, de tal forma que
, como antes, de tal forma que
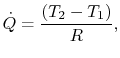
onde ![]() é dado por
é dado por
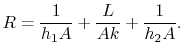 |
(17….21) |
Equação (17.21) é a resistência térmica para parede sólida com transferência de calor por convecção em cada lado.
Para uma pá de turbina num motor de turbina a gás, o arrefecimento é uma consideração crítica. Em termos da Figura 17.6, ![]() é a temperatura de saída do incinerador (entrada da turbina) e
é a temperatura de saída do incinerador (entrada da turbina) e ![]() é a temperatura à saída do compressor. Desejamos encontrar
é a temperatura à saída do compressor. Desejamos encontrar ![]() porque é a temperatura mais alta do metal. A partir de(17.20), a temperatura da parede pode ser escrita
porque é a temperatura mais alta do metal. A partir de(17.20), a temperatura da parede pode ser escrita
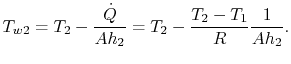 |
(17..22) |
br> usando a expressão para a resistência térmica, as temperaturas de parede podem ser expressas em termos de coeficientes de transferência de calor e propriedades de parede como
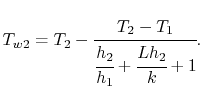 |
(17..23) |
br>Equação (17.23) fornece algumas linhas básicas de desenho. O objectivo é ter um valor baixo de ![]() . Isto significa
. Isto significa![]() deve ser grande,
deve ser grande, ![]() deve ser grande (mas podemos não ter tanta flexibilidade na escolha do material) e
deve ser grande (mas podemos não ter tanta flexibilidade na escolha do material) e ![]() deve ser pequeno. A forma de alcançar o primeiro destes é ter
deve ser pequeno. A forma de alcançar o primeiro destes é ter ![]() baixo (por exemplo,para escoar ar de arrefecimento como emFigure 17.1 para proteger a superfície).
baixo (por exemplo,para escoar ar de arrefecimento como emFigure 17.1 para proteger a superfície).
Um segundo exemplo de condução e convecção combinadas é dado por um cilindro exposto a um fluido fluido fluente. A geometria é mostrada emFigure 17.7.
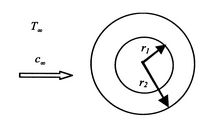
>br>>>/div>
Para a cilindro o fluxo de calor na superfície exterior é dado por
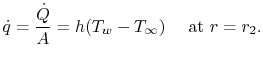
A condição limite na superfície interna pode ser uma condição de fluxo de calor ou uma especificação de temperatura; nós usamos esta última para simplificar a álgebra. Assim, ![]() at
at ![]() . Este é um modelo para a transferência de calor num tubo de raio
. Este é um modelo para a transferência de calor num tubo de raio ![]() surrounded by insulation of thickness
surrounded by insulation of thickness ![]() . A solução fora da região cilíndrica foi dada na secção 16.5.1 como
. A solução fora da região cilíndrica foi dada na secção 16.5.1 como
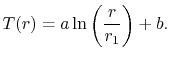
Utilização da condição de limite ![]() rendimentos
rendimentos ![]() .
.
Na interface entre o cilindro e o fluido, ![]() , a temperatura e o fluxo de calor são contínuos. (Pergunta: Porquê isto? Como discutiria o ponto?)
, a temperatura e o fluxo de calor são contínuos. (Pergunta: Porquê isto? Como discutiria o ponto?)
![$$displaystyle {q} = {-k=frac{dT}{dr}}_{substack{\i}_textrm{heat fl...... 2}{r_1}{r_1}{direito)+T_1{direito)-T_1-direito]-T_infty]} _\textrm{fluxo de calor à superfície para o fluido}$](https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img2033.png) |
(17..24) |
Plugging the form of the temperature distribution in the cylinderinto Equation (17.24) yields
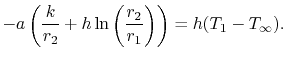
A constante de integração, ![]() , é
, é
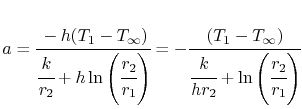
e a expressão para a temperatura é, em forma normalizada não-dimensional,
| (17..25) |
O fluxo de calor por unidade de comprimento, ![]() , é dado por
, é dado por
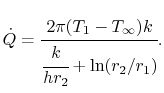 |
(17..26) |
br> As unidades na Equação (17,26) são W/m-s.
Um problema de interesse é escolher a espessura do isolamento tominimizar a perda de calor para uma diferença fixa de temperatura ![]() entre o interior do tubo e o fluido fluente distante do tubo. (
entre o interior do tubo e o fluido fluente distante do tubo. (![]() é a distribuição da temperatura de condução para o tubo). Para compreender o comportamento da transferência de calor, examinamos o denominador naEquação (17.26) como
é a distribuição da temperatura de condução para o tubo). Para compreender o comportamento da transferência de calor, examinamos o denominador naEquação (17.26) como ![]() varia. O isolamento do espessamento que dá a máxima transferência de calor é dado por
varia. O isolamento do espessamento que dá a máxima transferência de calor é dado por
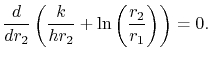 |
(17..27) |
(Pergunta: Como sabemos que isto é um máximo?)
Da Equação (17.27), o valor de ![]() para máximo
para máximo ![]() é assim
é assim
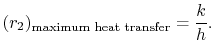 |
(17..28) |
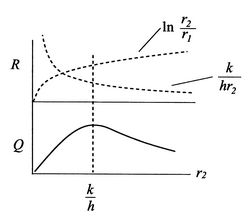
Se ![]() for inferior a isto, podemos adicionar isolamento e aumentar a perda de calor. Para compreender porque é que isto ocorre, considereFigure 17.8, que mostra aschematic da resistência térmica e da transferência de calor. Como
for inferior a isto, podemos adicionar isolamento e aumentar a perda de calor. Para compreender porque é que isto ocorre, considereFigure 17.8, que mostra aschematic da resistência térmica e da transferência de calor. Como ![]() aumento a partir de um valor inferior a
aumento a partir de um valor inferior a ![]() , ocorrem dois efeitos. Em primeiro lugar, a espessura do isolamento aumenta, tendendo a diminuir a transferência de calor porque o gradiente de temperatura diminui. Em segundo lugar, a área da superfície externa do isolamento aumenta, tendendo a aumentar a transferência de calor. O segundo destes é (vagamente) associado com o
, ocorrem dois efeitos. Em primeiro lugar, a espessura do isolamento aumenta, tendendo a diminuir a transferência de calor porque o gradiente de temperatura diminui. Em segundo lugar, a área da superfície externa do isolamento aumenta, tendendo a aumentar a transferência de calor. O segundo destes é (vagamente) associado com o ![]() termo, o primeiro com o termo. Existem assim dois efeitos concorrentes que se combinam para dar um máximo
termo, o primeiro com o termo. Existem assim dois efeitos concorrentes que se combinam para dar um máximo ![]() a
a ![]() .
.
>br>>>>p>>br>>Pontos de Lodo p>Na expressão ![]() , o que é
, o que é ![]() ? (MP 17.4)
? (MP 17.4)
Parece que temos muito convecção simplificada. Será realmente difícil encontrar o coeficiente de transferência de calor, ![]() ?(MP 17.5)
?(MP 17.5)
O que significa o “K” na fórmula da resistência de contacto?(MP 17.6)
Na equação para a temperatura num cilindro(17.25), o que é o “r?”(MP 17.7)
UnifiedTP
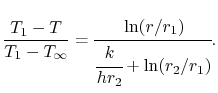 $\displaystyle \frac{T_1-T}{T_1-T_1-T_\i} = \cfrac{\i(r/r_1)}{cfrac{k}{hr_2}+\i(r_2/r_1)}.$
$\displaystyle \frac{T_1-T}{T_1-T_1-T_\i} = \cfrac{\i(r/r_1)}{cfrac{k}{hr_2}+\i(r_2/r_1)}.$