Zwaartepunt | Natuurondernemer

Computertekening van een verscheidenheid aan voorwerpen met het zwaartepunt - CG. CG = som van componentgewicht maal componentafstand gedeeld door totaalgewicht.

Het zwaartepunt is een geometrische eigenschap van elk voorwerp. Het zwaartepunt is de gemiddelde plaats van het gewicht van een voorwerp. We kunnen de beweging van een voorwerp door de ruimte volledig beschrijven in termen van de translatie van het zwaartepunt van het voorwerp van de ene plaats naar de andere, en de rotatie van het voorwerp om zijn zwaartepunt als het vrij kan roteren. Als het voorwerp alleen om een ander punt kan draaien, zoals bij een scharnier, dan kunnen we nog steeds de beweging van het voorwerp beschrijven. Tijdens de vlucht draaien zowel vliegtuigen als raketten om hun zwaartepunt. Een vlieger daarentegen draait om het brugpunt. Maar de trim van een vlieger hangt nog steeds af van de plaats van het zwaartepunt ten opzichte van het brugpunt, omdat voor elk voorwerp het gewicht altijd via het zwaartepunt werkt.

Het bepalen van het zwaartepunt is zeer belangrijk voor elk vliegend voorwerp.Hoe bepalen ingenieurs de plaats van het zwaartepunt voor een vliegtuig dat zij ontwerpen?

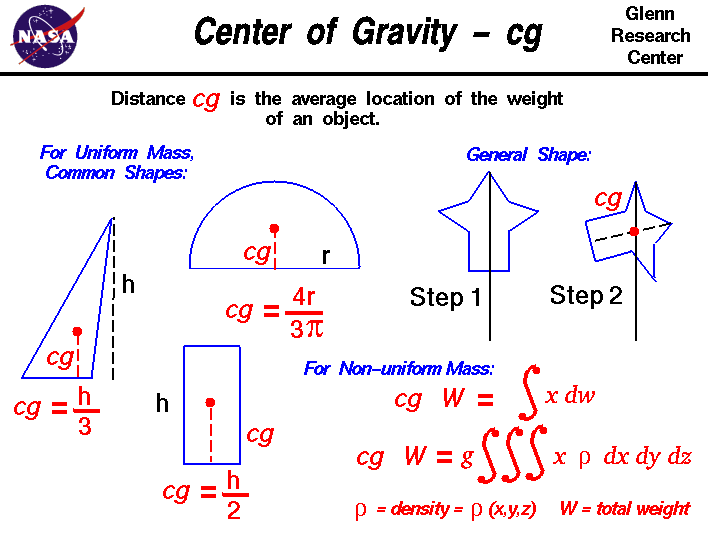
In het algemeen is het bepalen van het zwaartepunt (cg) een gecompliceerde procedure, omdat de massa (en het gewicht) mogelijk niet gelijkmatig over het voorwerp zijn verdeeld. Als de massa gelijkmatig verdeeld is, is het probleem veel eenvoudiger.Als het voorwerp een lijn (of vlak) van symmetrie heeft, ligt het zwaartepunt op de lijn van symmetrie.Voor een massief blok van gelijkmatig materiaal ligt het zwaartepunt eenvoudigweg op de gemiddelde plaats van de fysieke afmetingen. (Voor een rechthoekig blok van 50 X 20 X 10 ligt het zwaartepunt op het punt (25,10, 5) ).Voor een driehoek met hoogte h ligt het zwaartepunt op h/3, en voor een halve cirkel met straalr ligt het zwaartepunt op (4*r/(3*pi)) waarbij pi de verhouding is tussen de omtrek van de cirkel en de diameter. Er zijn tabellen met de ligging van het zwaartepunt voor vele eenvoudige vormen in wiskunde- en wetenschapsboeken.

Voor een voorwerp met een algemene vorm is er een eenvoudige mechanische manier om het zwaartepunt te bepalen:

Als we het voorwerp gewoon in evenwicht houden met behulp van een touwtje of een rand, dan is het punt waarop het voorwerp in evenwicht is het zwaartepunt. (Net als bij het balanceren van een potlood op je vinger!)
Een andere, meer ingewikkelde manier, is een methode in twee stappen die op de dia wordt getoond. In stap 1 hang je het voorwerp op aan een willekeurig punt en laat je vanaf datzelfde punt een verzwaard touw vallen. Trek een lijn op het voorwerp langs het touwtje. Voor stap 2 herhaal je de procedure vanaf een ander punt op het voorwerp. Je hebt nu twee lijnen op het voorwerp getekend die elkaar snijden. Het zwaartepunt is het punt waar de lijnen elkaar snijden. Deze procedure werkt goed voor onregelmatig gevormde voorwerpen die moeilijk in evenwicht te brengen zijn.

Als de massa van het voorwerp niet gelijkmatig verdeeld is, moeten we berekeningen gebruiken om het zwaartepunt te bepalen.We zullen het symbool S dw gebruiken om de integratie van een continue functie ten opzichte van het gewicht aan te geven. Dan kan het zwaartepunt worden bepaald uit:

cg * W = S x dw

waarbij x de afstand tot een referentielijn is, dw een gewichtstoename, enW het totale gewicht van het voorwerp. Om de rechterkant te evalueren, moeten we bepalen hoe het gewicht meetkundig varieert. Uit de gewichtsvergelijking weten we dat:

w = m * g

waarin m de massa van het voorwerp is, en g de gravitatieconstante. Op zijn beurt is de massa m van een voorwerp gelijk aan de dichtheid, rho, van het voorwerp maal het volume, V:

m = rho * V

We kunnen de laatste twee vergelijkingen combineren:

w = g * rho * V

daarna

dw = g * rho * dV

dw = g * rho(x,y,z) * dx dy dz

Als we een functionele vorm voor de massaverdeling hebben, kunnen we de formule voor het zwaartepunt oplossen:

cg * W = g * SSS x * rho(x,y,z) dx dy dz

waarbij SSS een drievoudige integraal aangeeft over dx. Als we de functionele vorm van de massaverdeling niet kennen, kunnen we de vergelijking numeriek integreren met behulp van een spreadsheet. Verdeel de afstand in een aantal kleine volume-segmenten en bepaal de gemiddelde waarde van het gewicht/volume (dichtheid maal zwaartekracht) over dat kleine segment. De som van de gemiddelde waarde van het gewicht/volume maal de afstand maal het volume gedeeld door het gewicht geeft het zwaartepunt.

Je kunt een filmpje bekijken van “Orville en Wilbur Wright” die uitleggen hoe het zwaartepunt de vlucht van hun vliegtuig beïnvloedde. Het filmbestand kan op uw computer worden opgeslagen en als podcast op uw podcastspeler worden bekeken.

Activiteiten:
iv id=”abc9fd028612-klasseiv id=”18111968cb12-activiteitiv id=”18111968cb12 activiteit
Geleide rondleidingen