De oorsprong van de geometrie
De eerste lijnen die de mens zich voorstelde waren rechte lijnen en cirkels. Deze markeerden de geboorte van de geometrie, wat letterlijk “aardmeting” betekent en ons een precies idee geeft van waar deze lijnen voor bedoeld waren. De eerste geometrie-experts waren landmeters in het oude Egypte. De Grieken noemden hen ‘arpedonapti’ – zij die touwen knopen. Egyptische deskundigen spanden touwen op het land om lijnen en cirkels te markeren. Sporen van dit oude gebruik zijn nog steeds aanwezig in vele moderne talen, zoals bijvoorbeeld in het gezegde “een lijn trekken”. Het gebruik van touwen voor landmetingen is eeuwenlang onveranderd gebleven en is ook in betrekkelijk recente tijden nog terug te vinden in het werk van landmeters.
Griekse historici getuigen van het ontstaan van de geometrie (letterlijk: aardmeting) in Egypte. Herodotus zegt:
Als de rivier eenvoudigweg de grenzen van het stuk land had opgeheven, was het de taak van de ambtenaren om de exacte scheidslijnen opnieuw te tekenen.
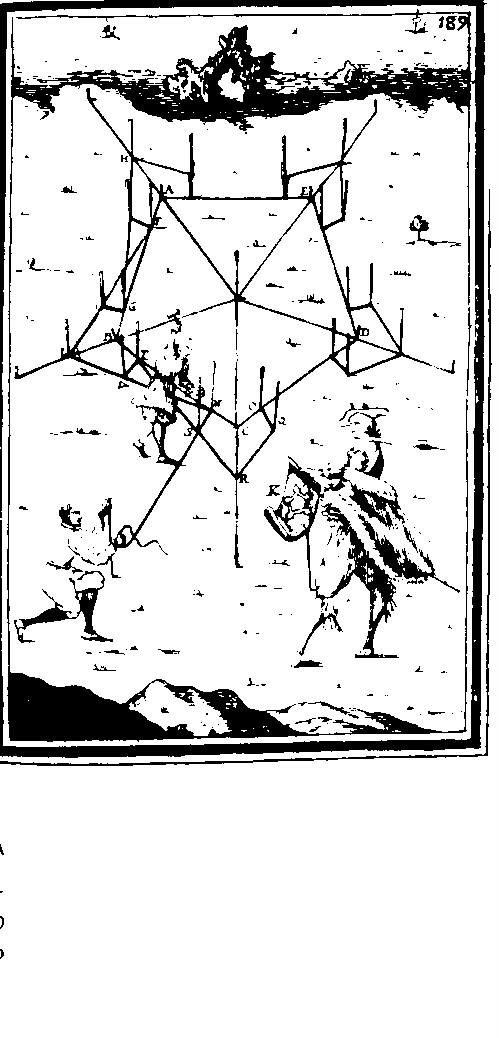 Egyptische meetkundigen werden “arpedonapti” genoemd, zij die touwen knoopten. Door touwen te spannen tekenden zij de twee eenvoudigste en belangrijkste lijnen in de meetkunde: de rechte lijn en de cirkel. De eerste is eenvoudigweg het spannen van een touw tussen twee punten, een soort operatie waarvan het beeld nog steeds aanwezig is in de uitdrukkingen “een lijn trekken”, “een loodlijn trekken”; de tweede is het laten draaien van een van de twee punten om het andere, dat vast wordt gehouden. Kon men zich de omvang van de ontwikkeling van deze twee elementaire praktijken voorstellen? Zeer waarschijnlijk niet. De praktische behoeften van de oude landmeters zouden al snel de noodzaak hebben doen ontstaan van het soort werk dat we tegenwoordig “met passer en vierkant” noemen en dat we eigenlijk “met cirkels en rechte lijnen” zouden moeten noemen.
Egyptische meetkundigen werden “arpedonapti” genoemd, zij die touwen knoopten. Door touwen te spannen tekenden zij de twee eenvoudigste en belangrijkste lijnen in de meetkunde: de rechte lijn en de cirkel. De eerste is eenvoudigweg het spannen van een touw tussen twee punten, een soort operatie waarvan het beeld nog steeds aanwezig is in de uitdrukkingen “een lijn trekken”, “een loodlijn trekken”; de tweede is het laten draaien van een van de twee punten om het andere, dat vast wordt gehouden. Kon men zich de omvang van de ontwikkeling van deze twee elementaire praktijken voorstellen? Zeer waarschijnlijk niet. De praktische behoeften van de oude landmeters zouden al snel de noodzaak hebben doen ontstaan van het soort werk dat we tegenwoordig “met passer en vierkant” noemen en dat we eigenlijk “met cirkels en rechte lijnen” zouden moeten noemen.
Heden ten dage is het zo vanzelfsprekend om papier als het natuurlijke terrein van de meetkunde te beschouwen, dat we het gebruik van alleen vierkanten en passers opvatten als een arbitraire limiet, ingevoerd door speculatieve geesten die de voorkeur gaven aan een klein aantal axioma’s boven het veelvoudige comfort dat voortvloeide uit de veelheid van instrumenten. Bijgevolg bestaat het verschil tussen de expert in theoretische meetkunde – ik heb het natuurlijk over de klassieke, euclidische – en de technicus – degene die de maten neemt, de architect – hoofdzakelijk in het feit dat de eerste vrijwillig besluit geen gebruik te maken van instrumenten, vierkanten en pantografen, die de tweede in zijn voordeel gebruikt.
Zo neigen wij ertoe de geometrie “in het veld” volledig te negeren ten gunste van die “op papier”, daarbij miskennend dat wanneer wij geometrische bewerkingen van het veld op papier overbrengen, zij soms totaal andere technieken en methoden vereisen.
Men mag niet over het hoofd zien dat de nauwkeurigheid van een plan veel noodzakelijker is in het veld (zowel voor degene die een stuk land opmeet en in stukken verdeelt, als voor de architect die gebouwen maakt – meestal zijn deze twee dezelfde persoon -) dan op papier. De architect die een duidelijk idee heeft van het totale plan en die zich herinnert welk proces hij heeft gevolgd om er doorheen te komen, zou een ontwerp nodig hebben. Zowel relatief recente als oude kaarten, die onvermijdelijk met onhandige instrumenten en hulpmiddelen zijn getekend, geven de grenzen van een stuk land niet exact weer. In feite is dit onmogelijk omdat zelfs een fout van een procentpunt – het minste dat op redelijk grote schaal kan voorkomen – een absolute vergissing zou opleveren die in het veld nauwelijks kan worden aanvaard. In dit geval zijn de kennis van de vorm en de afmetingen van het object dat moet worden beschreven (een veld, een gebouw) van fundamenteel belang; het is dan aan de meetkundige om op het veld de nauwkeurigheid weer te geven die op papier ontbreekt. Hetzelfde geldt voor de wiskundige voor wie de nauwkeurigheid van de cijfers helemaal niet nuttig is bij demonstraties. De geometrie op papier vervangt de nauwkeurigheid van de bewerkingen op het veld, door de geometrie van het mentale proces.
Integendeel, van de logica naar de materiële exactheid, als gevolg van de noodzakelijke schaalvergroting om van het plan over te gaan naar de eigenlijke schepping ervan, is de handeling van het spannen van een touw een van de belangrijkste handelingen gebleven sinds zo ver als het Oude Egypte en het Oude Griekenland. Deze praktijk is tot in de moderne tijd onveranderd gebleven, slechts voorbijgegaan door de uitvinding en de verbetering van bepaalde optische instrumenten. Terwijl het op papier vrij gemakkelijk is om een loodlijn te trekken met behulp van linialen en vierkanten, vereist dezelfde bewerking op het veld, met dezelfde graad van nauwkeurigheid, radicaal andere methoden. Op het veld is het vierkant nutteloos omdat het te klein is in verhouding tot de afmetingen van de vormen. Ook al is de vierkant uiterst nauwkeurig, de loodlijn die hij kan trekken zal hoogstens ongeveer een meter bedragen. Als we een vierkant van 30 meter per zijde moeten tekenen, moeten we deze lijn 30 keer verlengen. Dit zou zo’n onnauwkeurige bewerking zijn dat het waarschijnlijk tot dezelfde resultaten zou leiden als wanneer we de rechte hoek ruw opmeten.
 Deze overwegingen brengen ons terug bij de oorspronkelijke vraag: welke technieken gebruikten de Egyptische opmeters om een vierkant stuk land te tekenen? Hoe verkregen zij een vierkante hoek?
Deze overwegingen brengen ons terug bij de oorspronkelijke vraag: welke technieken gebruikten de Egyptische opmeters om een vierkant stuk land te tekenen? Hoe verkregen zij een vierkante hoek?
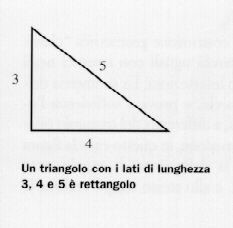
Zoals sommige geleerden hebben gesuggereerd, is het mogelijk dat zij kennis hadden van de stelling van Pythagoras (VIe eeuw v. Chr.) of, juister, het besef van zijn tegendeel, namelijk het feit dat een driehoek met zijden van 3, 4 en 5, waarin het kwadraat van de langste zijde gelijk is aan de som van de kwadraten van de andere twee zijden, een rechthoekige driehoek is. Indien men dus een ringtouw spant tot een lengte van 12 eenheden, gemarkeerd op drie punten op een afstand van 3, 4 en 5, naar de vorm van een driehoek met het hoekpunt in de gemarkeerde punten, dan is de hoek tussen de kortste zijden van de driehoek een rechte hoek.
Het is niet bekend of dit het proces was dat de landmeters in hun tijd gebruikten, want het is niet bewezen dat de oude Egyptenaren wisten dat de driehoek met zijden 3, 4 en 5 een rechthoekige driehoek is. Zelfs als zij hiervan op de hoogte waren, of van andere Pythagoras-driehoeken (zoals sterk wordt gesuggereerd door de aanwezigheid van verscheidene Pythagoras-driehoeken, zo niet in de Egyptische dan wel in de Babylonische wiskunde), dan nog impliceert dit dat zij de aard van de rechte hoek kenden, of op zijn minst wisten hoe deze te maken.
Waar kwam deze kennis vandaan? Vanwege het ontbreken van zelfs maar gedeeltelijke documentatie en getuigen, kunnen we proberen het probleem vanuit een ander gezichtspunt te benaderen, een wiskundige in plaats van een historische. De vraag die we moeten stellen is wat een rechte hoek anders maakt dan de andere? Of beter, wat is de bijzonderheid van de hoek van de driehoek met zijden 3, 4 en 5?
Het onmiddellijke antwoord is: in tegenstelling tot de andere driehoeken kunnen de driehoeken van Pythagoras, en vooral de eenvoudigste daarvan, die met de zijden 3, 4 en 5, in elkaar geschoven worden door ze aan de ene zijde te draaien en dan weer aan de andere zijde. Op deze manier verkrijgt men een symmetrische configuratie die alle beschikbare ruimte volledig opvult zonder overlappingen of tussenruimten.
 Geen andere hoek dan de rechte heeft deze symmetrische eigenschap, die zijn eigen definitie krijgt in het eerste complete meetkundeboek dat ooit onze tijd bereikte, Euclides’ Elementen (IV eeuw v.Chr.):
Geen andere hoek dan de rechte heeft deze symmetrische eigenschap, die zijn eigen definitie krijgt in het eerste complete meetkundeboek dat ooit onze tijd bereikte, Euclides’ Elementen (IV eeuw v.Chr.):
Als een rechte lijn die op een andere valt gelijke hoeken vormt, zijn dit beide rechte hoeken.
De aard van de kwadratische hoek ligt in het feit dat de hoeken die ontstaan door het snijpunt van twee rechte lijnen gelijk zijn. Dit kan onmiddellijk op papier worden aangetoond door het papier langs een van de convergerende lijnen te vouwen en na te gaan of de andere lijn op zichzelf vouwt.
De “klassieke” meetkundige constructie die bestaat uit het markeren van twee cirkels en vervolgens hun snijpunten te verenigen bezit deze eigenschap ook. Het symmetrische karakter van de vorm is overduidelijk, en het is een duidelijk bewijs van de gelijkheid van de hoeken. Bovendien, in tegenstelling tot de Pythagoras-driehoek die een verdere constructie nodig heeft, suggereert de vorm in dit geval onmiddellijk de definitie van de kwadratische hoek door de gelijkheid van de hoeken en construeert tegelijkertijd zichzelf.
Dit zijn nog steeds eenvoudige veronderstellingen. Zonder enige twijfel is dit proces veel eenvoudiger en nauwkeuriger dan het eerste. Men zou kunnen zeggen dat we op deze manier alleen de loodlijn kunnen markeren die door het middelpunt van het gegeven lijnstuk gaat, ook wel de as van dit lijnstuk genoemd. Niettemin is het niet moeilijk op te merken dat als we een loodlijn nodig hebben aan een uiteinde, zoals in het geval van het tekenen van een vierkant, het nodig zal zijn het lijnstuk te verdubbelen en het te verlengen naar de plaats waar we de loodlijn willen tekenen en dan het voorgaande proces te herhalen.Het is noodzakelijk op te merken dat al deze technieken bijzonder geschikt zijn voor vlak land zoals de Egyptische vlakte.