Een correlatie- of eenvoudige lineaire regressieanalyse kan bepalen of twee numerieke variabelen significant lineair met elkaar zijn verbonden. Een correlatieanalyse geeft informatie over de sterkte en de richting van het lineaire verband tussen twee variabelen, terwijl een eenvoudige lineaire regressieanalyse de parameters in een lineaire vergelijking schat die kan worden gebruikt om de waarden van de ene variabele te voorspellen op basis van de andere.
Correlatie
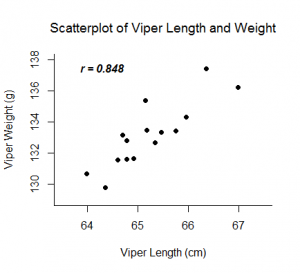
De Pearson-correlatiecoëfficiënt, r, kan waarden aannemen tussen -1 en 1. Hoe verder r van nul af ligt, hoe sterker het lineaire verband tussen de twee variabelen. Het teken van r komt overeen met de richting van het verband. Als r positief is, neemt de andere toe naarmate de ene variabele toeneemt. Als r negatief is, heeft de ene variabele de neiging toe te nemen en de andere af te nemen. Een perfect lineair verband (r=-1 of r=1) betekent dat een van de variabelen perfect kan worden verklaard door een lineaire functie van de andere.
Voorbeelden:

Lineaire regressie
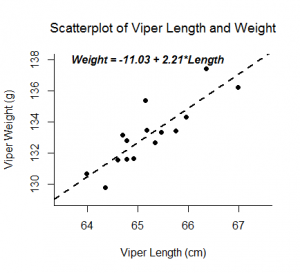
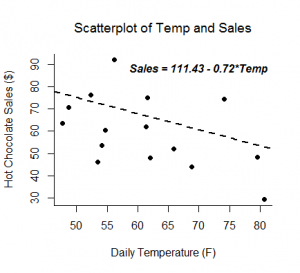
Een lineaire regressieanalyse levert schattingen op voor de helling en de intercept van de lineaire vergelijking die een uitkomstvariabele, Y, voorspelt op basis van de waarden van een voorspellende variabele, X. Een algemene vorm van deze vergelijking wordt hieronder weergegeven:
![]()
Het intercept, b0, is de voorspelde waarde van Y wanneer X=0. De helling, b1, is de gemiddelde verandering in Y voor elke toename van X met één eenheid. Behalve dat de schatting van de helling u de sterkte en richting van het lineaire verband tussen X en Y geeft, maakt deze vergelijking ook een interpretatie mogelijk van hoe Y verandert wanneer X toeneemt. Deze vergelijking kan ook worden gebruikt om waarden van Y te voorspellen voor een waarde van X.
Voorbeelden:
Inferentiële tests
Inferentiële tests kunnen worden uitgevoerd op zowel de correlatie- als de hellingschattingen die zijn berekend op basis van een aselecte steekproef uit een populatie. Beide analyses zijn t-toetsen die worden uitgevoerd op de nulhypothese dat de twee variabelen niet lineair gerelateerd zijn. Indien uitgevoerd op dezelfde gegevens, leveren een correlatietest en hellingtest dezelfde teststatistiek en p-waarde op.
Aannames:
- Random steekproeven
- Onafhankelijke waarnemingen
- De predictorvariabele en uitkomstvariabele zijn lineair gerelateerd (beoordeeld door visuele controle van een scatterplot).
- De populatie van waarden voor de uitkomst is normaal verdeeld voor elke waarde van de voorspeller (beoordeeld door de normaliteit van de residuen te bevestigen).
- De variantie van de verdeling van de uitkomst is gelijk voor alle waarden van de voorspeller (beoordeeld door een residuplot visueel te controleren op een funnelingpatroon).
Hypothesen:
Ho: De twee variabelen zijn niet lineair gerelateerd.
Ha: De twee variabelen zijn lineair gerelateerd.
Relevante vergelijkingen:
Vrijheidsgraden: df = n-2

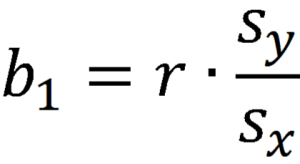
![]()
Voorbeeld 1: Handberekening
Deze video’s onderzoeken het lineaire verband tussen de lengte van mensen en de gemeten spanwijdte van hun armen.
Correlatie:


Regressie:


Steekproefconclusie: Wanneer we het verband tussen de spanwijdte en de lichaamslengte onderzoeken, vinden we een grote positieve correlatie (r=.95), wat duidt op een sterk positief lineair verband tussen de twee variabelen. Wij berekenden de vergelijking voor de best passende lijn als Armspan=-1.27+1.01(Lengte). Dit betekent dat voor een persoon die 0 inch lang is, de voorspelde armspanwijdte -1,27 inch zou zijn. Dit is geen mogelijke waarde omdat het bereik van onze gegevens veel groter zal zijn. Voor elke centimeter toename in lengte wordt een toename van de spanwijdte met 1,01 centimeter voorspeld.
Voorbeeld 2: Analyse uitvoeren in Excel 2016
Voor sommige van deze analyses moet u de invoegtoepassing Data Analysis ToolPak in Excel hebben ingeschakeld. Ga voor instructies over het uitvoeren van deze analyse in eerdere versies van Excel naar https://stat.utexas.edu/videos
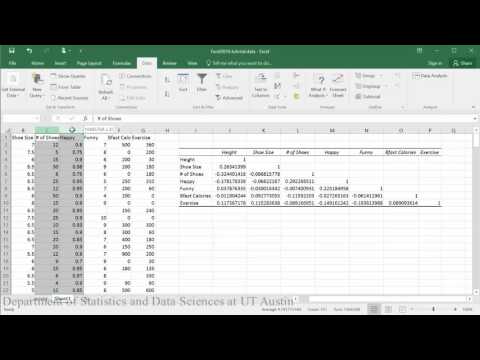
Dataset gebruikt in video’s
Correlatiematrix en p-waarde:
PDF-richtingen behorende bij video

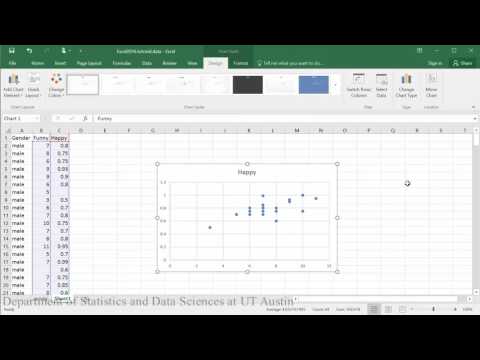
Creëren van scatterplots:
PDF-aanwijzingen die overeenkomen met video

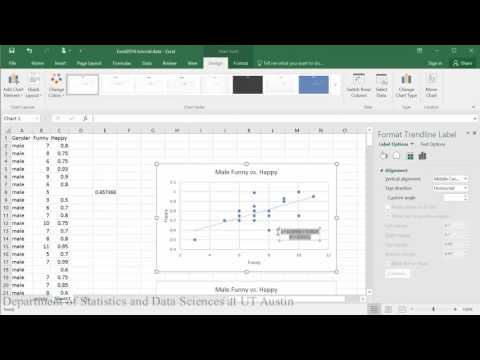
Lineair model (eerste helft van tutorial):
PDF-aanwijzingen bij video

Residuele plots maken:
PDF-aanwijzingen bij video
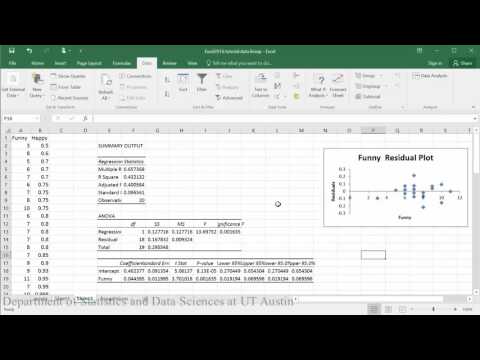

Voorbeeldconclusie: Bij het evalueren van het verband tussen hoe gelukkig iemand is en hoe grappig anderen hem of haar beoordeelden, geeft de scatterplot aan dat er een matig sterk positief lineair verband tussen de twee variabelen lijkt te bestaan, wat wordt ondersteund door de correlatiecoëfficiënt (r = .65). Een controle van de veronderstellingen met behulp van de residuplot gaf geen problemen met de gegevens aan. De lineaire vergelijking voor het voorspellen van happy uit funny was Happy=.04+0.46(Funny). Het y-afbakeningspunt geeft aan dat voor een persoon wiens score voor grappig nul was, zijn geluk wordt voorspeld als .04. De score voor grappig voorspelt significant meer geluk, zodat voor elke 1 punt stijging van de score voor grappig de mannen een toename van .46 in geluk voorspeld wordt (t = 3.70, p = .002).
Voorbeeld 3: Analyse uitvoeren in R
De volgende video’s onderzoeken de relatie tussen BMI en bloeddruk voor een steekproef van medische patiënten.
Dataset gebruikt in video’s
Correlatie:
R scriptbestand gebruikt in video
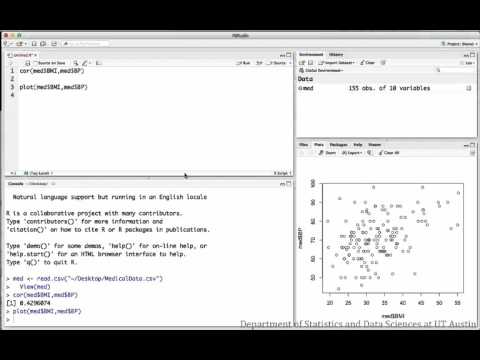

Regressie:
R scriptbestand gebruikt in video