Le origini della geometria
Le prime linee che l’uomo immaginò furono linee rette e cerchi. Queste segnarono la nascita della geometria, che significa letteralmente “misura della terra”, dandoci un’idea precisa di ciò a cui queste linee erano destinate. I primi esperti di geometria furono gli agrimensori nell’antico Egitto. I greci li chiamano ‘arpedonapti’, coloro che annodano le corde. Gli esperti egiziani usavano stringere delle corde sulla terra per segnare linee e cerchi. Tracce di questo antico uso sono ancora presenti in molte lingue moderne come, per esempio, nel detto “tracciare una linea”. L’impiego di corde per le operazioni di misurazione del terreno è rimasto inalterato per diversi secoli e si può ancora trovare nel lavoro degli agrimensori in tempi relativamente recenti.
Gli storici greci testimoniano la nascita della geometria (letteralmente: misurazione della terra) in Egitto. Erodoto dice:
Se il fiume aveva semplicemente cancellato i confini del pezzo di terra, era compito dei funzionari ridisegnare le divisioni esatte.
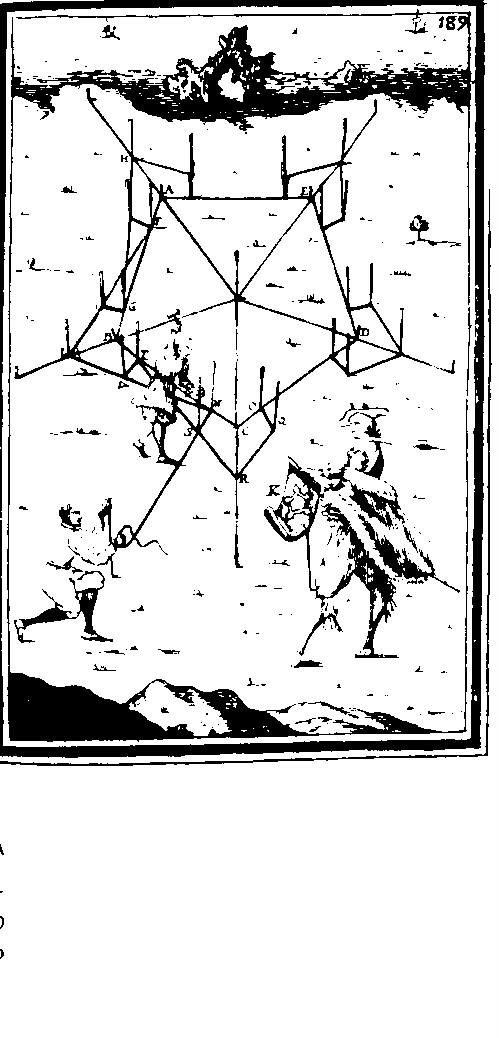 Gli esperti egizi di geometria erano chiamati “arpedonapti”, coloro che annodano le corde. È stringendo le corde che hanno disegnato le due linee più semplici e più importanti della geometria: la linea retta e il cerchio. La prima, semplicemente stringendo una corda tra due punti, un tipo di operazione la cui immagine è ancora presente nelle espressioni “disegnare una linea”, “disegnare una perpendicolare”; la seconda, facendo girare uno dei due punti intorno all’altro che è tenuto fisso. Potevano immaginare la portata dello sviluppo di queste due pratiche elementari? Molto probabilmente no. Infatti le necessità pratiche degli antichi misuratori terrestri fecero emergere ben presto la necessità di lavori del tipo che oggi chiamiamo “con squadra e compasso” e che più propriamente dovrebbero essere chiamati “con cerchi e linee rette”.
Gli esperti egizi di geometria erano chiamati “arpedonapti”, coloro che annodano le corde. È stringendo le corde che hanno disegnato le due linee più semplici e più importanti della geometria: la linea retta e il cerchio. La prima, semplicemente stringendo una corda tra due punti, un tipo di operazione la cui immagine è ancora presente nelle espressioni “disegnare una linea”, “disegnare una perpendicolare”; la seconda, facendo girare uno dei due punti intorno all’altro che è tenuto fisso. Potevano immaginare la portata dello sviluppo di queste due pratiche elementari? Molto probabilmente no. Infatti le necessità pratiche degli antichi misuratori terrestri fecero emergere ben presto la necessità di lavori del tipo che oggi chiamiamo “con squadra e compasso” e che più propriamente dovrebbero essere chiamati “con cerchi e linee rette”.
Al giorno d’oggi, è così naturale considerare la carta come l’arena naturale della geometria, che concepiamo l’uso della sola squadra e del compasso come un limite arbitrario introdotto da spiriti speculativi che preferivano qualche numero di assiomi alla molteplicità di comodità derivanti dalla molteplicità degli strumenti. Di conseguenza, la differenza tra l’esperto di geometria teorica -mi riferisco naturalmente a quella classica euclidea- e il tecnico -quello che prende le misure, l’architetto- risiede principalmente nel fatto che il primo decide, volontariamente, di non usare strumenti, piazze e pantografi, che il secondo usa a suo vantaggio.
In questo modo, si tende ad ignorare completamente la geometria “sul campo” a favore di quella “sulla carta”, non riconoscendo che quando si trasferiscono le operazioni geometriche dal campo alla carta, queste richiedono tecniche e metodi a volte totalmente diversi.
Non bisogna trascurare il fatto che la precisione di un piano è molto più necessaria sul campo (a colui che misura e divide in parti un pezzo di terra, così come all’architetto che fa edifici -il più delle volte si tratta della stessa persona-) che sulla carta; l’architetto che ha un’idea chiara del piano generale e che ricorda il processo che ha seguito per realizzarlo avrebbe bisogno di una bozza. Sia le mappe relativamente recenti che quelle vecchie, inevitabilmente disegnate con strumenti e supporti rudimentali, non riproducono esattamente i confini di un pezzo di terra. Infatti, questo è impossibile perché anche un errore di un punto percentuale – il minimo che potrebbe verificarsi in una scala ragionevolmente grande – darebbe vita a un errore assoluto che difficilmente potrebbe essere accettato sul campo. In questo caso, la conoscenza della forma e delle misure dell’oggetto da descrivere (un campo, un edificio), sono fondamentali; sarà poi compito dell’esperto di geometria riprodurre sul campo la precisione che manca sulla carta. Lo stesso accade al matematico al quale la precisione delle figure non è affatto utile nelle dimostrazioni. La geometria sulla carta sostituisce la precisione delle operazioni sul campo, con la geometria del processo mentale.
Al contrario, dalla logica all’esattezza materiale, come conseguenza del necessario allargamento di scala per passare dal progetto alla realizzazione effettiva di esso, l’azione di tendere una corda è rimasta una delle principali operazioni fino all’antico Egitto e all’antica Grecia. Questa pratica è rimasta inalterata fino ai tempi moderni, superati solo dall’invenzione e dal miglioramento di certi strumenti ottici. Mentre, sulla carta, è abbastanza facile disegnare una perpendicolare per mezzo di righelli e squadre, la stessa operazione sul campo, con lo stesso grado di precisione, richiede metodi radicalmente diversi. Sul campo la squadra è inutile perché è troppo piccola rispetto alle dimensioni delle forme. Anche se la squadra è estremamente precisa, la perpendicolare che può tracciare raggiungerà al massimo più o meno un metro. Se dobbiamo segnare un quadrato di 30 metri per lato, dobbiamo prolungare questa linea 30 volte. Questa sarebbe un’operazione così inesatta che probabilmente darebbe i risultati come se misurassimo l’angolo retto in modo approssimativo.
 Queste riflessioni ci riportano alla domanda iniziale: quali tecniche usavano i misuratori egiziani per disegnare un pezzo di terra quadrato? Come ottenevano un angolo quadrato?
Queste riflessioni ci riportano alla domanda iniziale: quali tecniche usavano i misuratori egiziani per disegnare un pezzo di terra quadrato? Come ottenevano un angolo quadrato?
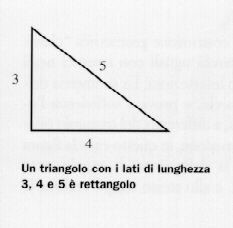
Come hanno suggerito alcuni studiosi, è possibile che avessero la conoscenza del teorema di Pitagora (VI secolo a.C.) o, più precisamente, la consapevolezza del suo contrario, cioè il fatto che un triangolo con i lati che misurano 3, 4 e 5, in cui il quadrato del lato maggiore è uguale alla somma dei quadrati degli altri due lati, è un triangolo rettangolo. Perciò, se tendiamo una corda ad anello della lunghezza di 12 unità, segnata in tre punti alla distanza di 3, 4 e 5, verso la forma di un triangolo con il vertice nei punti segnati, l’angolo tra i lati più corti del triangolo è un angolo retto.
Non si sa se questo era il procedimento che gli antichi agrimensori usavano ai loro tempi, poiché non è stato provato che gli antichi egizi sapessero che il triangolo con i lati 3, 4 e 5 è un triangolo rettangolo. Anche se erano a conoscenza di questo, o di altri triangoli pitagorici (come è fortemente suggerito dalla presenza di diversi triangoli pitagorici, se non nella matematica egiziana, allora in quella babilonese), questo implica necessariamente che conoscevano la natura di, o almeno come creare l’angolo retto.
Da dove veniva questa conoscenza? A causa della mancanza di documentazione anche parziale e di testimoni, possiamo provare ad affrontare il problema da un punto di vista diverso, matematico piuttosto che storico. La domanda che dobbiamo porci è cosa rende un angolo retto diverso dagli altri? O meglio, qual è la peculiarità dell’angolo del triangolo con lati 3, 4 e 5?
La risposta immediata è: a differenza degli altri triangoli, quelli pitagorici e in particolare il più semplice di essi, quello con i lati 3, 4 e 5, possono essere fatti combaciare girandoli da un lato e poi di nuovo dall’altro. In questo modo, si ottiene una configurazione simmetrica che riempie totalmente tutto lo spazio disponibile senza sovrapposizioni o spazi vuoti.
 Nessun altro angolo se non quello retto ha questa caratteristica simmetrica che diventa la sua propria definizione nel primo libro completo di geometria mai giunto ai nostri tempi, gli Elementi di Euclide (IV secolo a.C.):
Nessun altro angolo se non quello retto ha questa caratteristica simmetrica che diventa la sua propria definizione nel primo libro completo di geometria mai giunto ai nostri tempi, gli Elementi di Euclide (IV secolo a.C.):
Quando una retta che cade su un’altra forma angoli uguali, questi sono entrambi retti.
La natura dell’angolo quadrato risiede nel fatto che gli angoli risultanti dall’intersezione di due rette sono uguali. Questo può essere immediatamente dimostrato sulla carta piegando la carta lungo una delle linee convergenti e verificando che l’altra linea si ripiega su se stessa.
Anche la costruzione geometrica “classica” che consiste nel segnare due cerchi e poi unificare le loro intersezioni possiede questa proprietà: il carattere simmetrico della forma è abbastanza evidente, ed è una chiara prova dell’uguaglianza degli angoli. Inoltre, a differenza del triangolo di Pitagora che ha bisogno di un’ulteriore costruzione, in questo caso la forma suggerisce immediatamente la definizione di angolo quadrato attraverso l’uguaglianza degli angoli e, allo stesso tempo, si costruisce da sola.
Queste sono ancora semplici supposizioni. Senza dubbio, questo processo è decisamente più semplice e più preciso del primo. Si potrebbe dire che in questo modo possiamo solo segnare la perpendicolare che passa per il centro del segmento dato, chiamato anche asse del segmento. Tuttavia, non è difficile notare che se abbiamo bisogno di una perpendicolare ad un estremo, come nel caso del disegno di un quadrato, sarà necessario raddoppiare il segmento prolungandolo verso il punto in cui vogliamo disegnare la perpendicolare e poi ripetere il processo precedente.
È necessario osservare che tutte queste tecniche sono particolarmente adatte per terreni piani come la pianura egiziana.