PEMDASExamplesUn problema
Purplemath
Se ti viene chiesto di semplificare qualcosa come “4 + 2×3”, la domanda che sorge spontanea è “In che modo lo faccio? Perché ci sono due opzioni!”. Potrei aggiungere prima:
4 + 2×3 = (4 + 2)×3 = 6×3 = 18
…oppure potrei moltiplicare prima:
4 + 2×3 = 4 + (2×3) = 4 + 6 = 10
Quale risposta è quella giusta?
Il contenuto continua sotto
MathHelp.com

Sembra che la risposta dipenda dal modo in cui si guarda il problema. Ma non possiamo avere questo tipo di flessibilità in matematica; la matematica non funziona se non si può essere sicuri della risposta, o se la stessa espressione può essere calcolata in modo da arrivare a due o più risposte diverse.
Affiliato
Per eliminare questa confusione, abbiamo delle regole di precedenza, stabilite almeno a partire dal 1500, chiamate “ordine delle operazioni”. Le “operazioni” sono l’addizione, la sottrazione, la moltiplicazione, la divisione, l’esponenziazione e il raggruppamento; l'”ordine” di queste operazioni stabilisce quali operazioni hanno la precedenza (sono curate) prima di quali altre operazioni.
Una tecnica comune per ricordare l’ordine delle operazioni è l’abbreviazione (o, più correttamente, l'”acronimo”) “PEMDAS”, che si trasforma nella frase mnemonica “Please Excuse My Dear Aunt Sally”. Questa frase sta per, e aiuta a ricordare l’ordine di “Parentesi, Esponenti, Moltiplicazione e Divisione, e Addizione e Sottrazione”. Questo elenco ti dice il rango delle operazioni: Le parentesi superano gli esponenti, che superano la moltiplicazione e la divisione (ma la moltiplicazione e la divisione sono allo stesso livello), e la moltiplicazione e la divisione superano l’addizione e la sottrazione (che sono insieme al livello inferiore). In altre parole, la precedenza è:
- Parentesi (semplificare al loro interno)
- Esponenti
- Moltiplicazione e divisione (da sinistra a destra)
- Addizione e sottrazione (da sinistra a destra)
Quando si ha un gruppo di operazioni dello stesso grado, si opera semplicemente da sinistra a destra. Per esempio, 15 ÷ 3 × 4 non è 15 ÷ (3 × 4) = 15 ÷ 12, ma è piuttosto (15 ÷ 3) × 4 = 5 × 4, perché, andando da sinistra a destra, si arriva prima al segno di divisione.
Se non siete sicuri di questo, provatelo nella vostra calcolatrice, che è stata programmata con la gerarchia dell’Ordine delle operazioni. Per esempio, digitando l’espressione di cui sopra in una calcolatrice grafica, si otterrà:

Utilizzando la gerarchia di cui sopra, vediamo che, nella domanda “4 + 2×3” all’inizio di questo articolo, la scelta 2 era la risposta corretta, perché dobbiamo fare la moltiplicazione prima di fare l’addizione.
Continua sotto
(Nota: I parlanti di inglese britannico spesso usano invece l’acronimo “BODMAS”, piuttosto che “PEMDAS”. BODMAS sta per “Brackets, Orders, Division and Multiplication, and Addition and Subtraction”. Poiché le “parentesi” sono la stessa cosa delle parentesi e gli “ordini” sono la stessa cosa degli esponenti, i due acronimi significano la stessa cosa. Inoltre, si può vedere che la “M” e la “D” sono invertite nella versione britannica-inglese; questo conferma che la moltiplicazione e la divisione sono allo stesso “grado” o “livello”. Gli anglofoni canadesi dividono la differenza, usando BEDMAS.)
L’ordine delle operazioni è stato stabilito per evitare errori di comunicazione, ma PEMDAS può generare la propria confusione; alcuni studenti a volte tendono ad applicare la gerarchia come se tutte le operazioni in un problema fossero allo stesso “livello” (semplicemente andando da sinistra a destra), ma spesso queste operazioni non sono “uguali”. Molte volte aiuta lavorare i problemi dall’interno verso l’esterno, piuttosto che da sinistra a destra, perché spesso alcune parti del problema sono “più in basso” di altre parti. Il modo migliore per spiegarlo è fare alcuni esempi:
-
Semplificare 4 + 32.
Ho bisogno di semplificare il termine con l’esponente prima di provare ad aggiungere il 4:
4 + 32 = 4 + 9 = 13
-
Semplificare 4 + (2 + 1)2.
Devo semplificare dentro le parentesi prima di poter prendere l’esponente. Solo allora posso fare l’addizione del 4.
4 + (2 + 1)2 = 4 + (3)2 = 4 + 9 = 13
Advertisement
-
Semplifica 4 + 2.
Affiliazione
Non dovrei provare a fare queste parentesi annidate da sinistra a destra; quel metodo è semplicemente troppo soggetto a errori. Invece, proverò a lavorare dall’interno verso l’esterno. Prima semplificherò all’interno delle parentesi graffe, poi semplificherò all’interno delle parentesi quadre, e solo allora mi occuperò della squadratura. Fatto questo, posso finalmente aggiungere il 4:
4 + 2
= 4 + 2
= 4 + 2
= 4 + 9
= 13
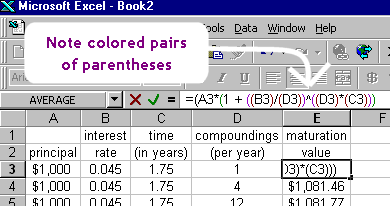
Non c’è un significato particolare nell’uso delle parentesi quadre (il “” sopra) al posto delle parentesi. Le parentesi e le parentesi graffe (i caratteri “{” e “}”) si usano quando ci sono parentesi annidate, come aiuto per tenere traccia di quali parentesi vanno con quali. I diversi caratteri di raggruppamento sono usati solo per comodità. Questo è simile a quello che succede in un foglio di calcolo di Excel quando si inserisce una formula usando le parentesi: ogni serie di parentesi è codificata a colori, così si possono distinguere le coppie:
-
Semplificare
Semplificherò prima all’interno delle parentesi:
Quindi la mia risposta semplificata è
La prossima pagina ha altri esempi lavorati….
URL: https://www.purplemath.com/modules/orderops.htm
Pagina 1Pagina 2Pagina 3