Concetti di statistica

Proprietà di r

Discutiamo e illustriamo ora diverse importanti proprietà del coefficiente di correlazione come misura numerica della forza di una relazione lineare.

1. La correlazione non cambia quando cambiano le unità di misura di una delle due variabili. In altre parole, se cambiamo le unità di misura della variabile esplicativa e/o della variabile di risposta, non ha alcun effetto sulla correlazione (r).

Per illustrare, confrontare le due versioni dello scatterplot della relazione tra l’età di un guidatore e la distanza massima per leggere un cartello autostradale.

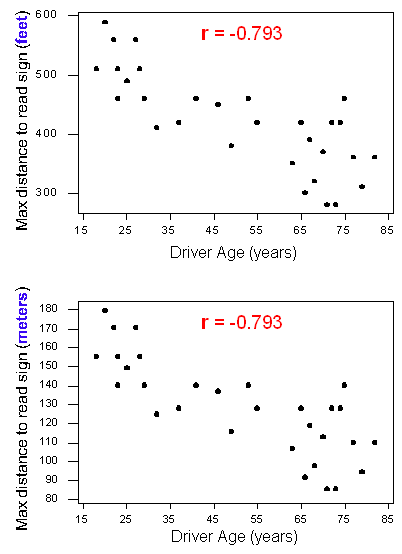
Lo scatterplot in alto mostra i dati originali dove le distanze massime sono misurate in piedi. Lo scatterplot inferiore mostra la stessa relazione, ma con le distanze massime cambiate in metri. Notate che i valori y sono cambiati, ma le correlazioni sono le stesse. Questo esempio illustra che un cambiamento di unità non cambia r. Questo è vero anche se cambiamo le unità di entrambe le variabili. Ha senso perché un cambiamento di unità non cambia il modello nei dati. La direzione, la forma e la forza della relazione rimangono le stesse. Poiché r misura la direzione e la forza di una relazione lineare, il valore di r rimane lo stesso.

2. La correlazione misura solo la forza di una relazione lineare tra due variabili. Ignora qualsiasi altro tipo di relazione, non importa quanto sia forte. Per esempio, si consideri la relazione tra il consumo medio di carburante nel percorrere una distanza fissa in un’auto e la velocità alla quale l’auto guida:

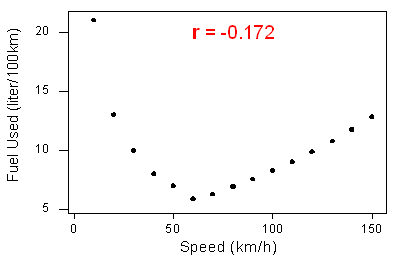
I dati hanno una forma curvilinea regolare. La relazione è molto forte perché i dati seguono perfettamente la curva.

Nota che la correlazione r = -0,172 indica una relazione lineare debole. Questo ha senso perché i dati non seguono strettamente una forma lineare. Quindi il coefficiente di correlazione dà solo informazioni sulla forza di una relazione lineare. Non dà informazioni affidabili sulla forza di una relazione curvilinea.

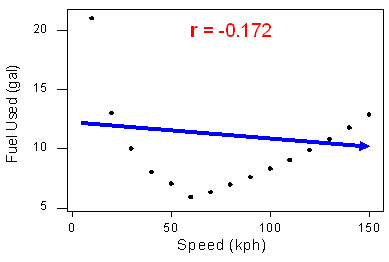
Questo esempio illustra che il coefficiente di correlazione è inutile come misura della forza se la relazione non è lineare. Illustra anche una regola importante: Fare sempre uno scatterplot dei dati prima di calcolare e interpretare il significato di r.

Perché dovremmo fare prima uno scatterplot? Se non guardassimo lo scatterplot, ma guardassimo solo r, quale errore potremmo commettere? Potremmo concludere che la relazione tra le variabili è debole (o che non c’è alcuna relazione) perché r è vicino a zero. Ma questa conclusione è sbagliata. Abbiamo interpretato erroneamente “r vicino a 0” come un indicatore di una relazione debole o di nessuna relazione piuttosto che di una relazione lineare debole o di nessuna relazione lineare. Possiamo facilmente evitare questa errata interpretazione di r guardando il grafico di dispersione.

Riassumiamo. Se r è vicino allo zero, significa che i dati hanno una relazione lineare molto debole o nessuna relazione lineare. Quando r è vicino a zero, è possibile che i dati abbiano una forte relazione curvilinea (come abbiamo visto in questo esempio). Per evitare errori, dobbiamo guardare la forma dei dati nello scatterplot prima di calcolare e interpretare r. Se la forma non è lineare, non usare r.

3. La correlazione da sola non è sufficiente a determinare se una relazione è lineare. Per vedere questo, guardiamo una situazione con un valore di r che è vicino a 1 ma una relazione che non è lineare. Ricordiamo lo studio in cui i partecipanti sono stati pagati per completare un sondaggio. Lo studio ha esaminato la relazione tra l’importo dell’incentivo monetario e la percentuale del campione che ha restituito il sondaggio.

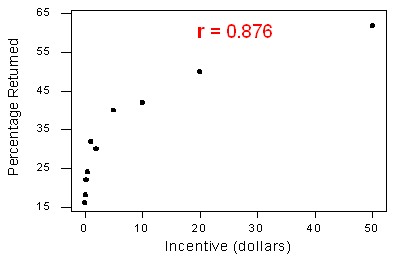
Le variabili hanno una forte relazione curvilinea, ma la correlazione è r = 0.876, abbastanza vicino a 1.

Ripercorrendo gli ultimi due esempi, vediamo che le forti relazioni curvilinee possono avere una correlazione vicina a 0 o vicina a 1. Quindi la sola correlazione non ci dice se una relazione è lineare. Dobbiamo guardare uno scatterplot dei dati.

Guarda sempre i dati!

4. La correlazione è fortemente influenzata dai valori anomali. Come imparerete nelle prossime due attività, il modo in cui l’outlier influenza la correlazione dipende dal fatto che l’outlier sia o meno coerente con lo schema della relazione lineare.

Utilizzando la simulazione qui sotto, esploriamo come un outlier influenza la correlazione.

Clicca qui per aprire questa simulazione nella sua propria finestra.

Per vedere come un outlier influenza la correlazione, fate come segue:

1. Riempite il grafico di dispersione con un’ipotetica relazione lineare positiva tra X e Y (cliccando sul grafico una dozzina di volte a partire dal basso a sinistra e salendo in diagonale verso l’alto a destra). Fai attenzione al coefficiente di correlazione calcolato in alto a sinistra della simulazione. (Cliccando sul bidone della spazzatura potete ricominciare da capo).
2. Una volta che siete soddisfatti dei vostri dati ipotetici, create un outlier cliccando su uno dei punti dati in alto a destra del grafico e trascinandolo in basso lungo il lato destro del grafico. Di nuovo, presta attenzione a cosa succede al valore della correlazione.

Cosa ha illustrato questa attività? Questa attività illustra che la correlazione diminuisce quando l’outlier si discosta dal modello della relazione. Trascinando un punto di dati dall’alto a destra in basso a destra, avete creato un outlier che non si adatta all’associazione positiva nel resto dei dati. Questo diminuisce la forza della relazione lineare e causa una diminuzione di r.

Nella prossima attività, vedrete come la correlazione aumenta quando l’outlier è coerente con la direzione della relazione lineare.

Riassumiamo

• Un caso speciale della relazione tra due variabili quantitative è la relazione lineare in cui una linea retta riassume semplicemente e adeguatamente la relazione.
• Quando il grafico di dispersione mostra una relazione lineare, lo completiamo con il coefficiente di correlazione (r), che misura la forza e la direzione di una relazione lineare tra due variabili quantitative. La correlazione varia tra -1 e 1. Valori vicini a -1 indicano una forte relazione lineare negativa, valori vicini a 0 indicano una relazione lineare debole, e valori vicini a 1 indicano una forte relazione lineare positiva.
• La correlazione è una misura numerica appropriata solo per le relazioni lineari ed è sensibile ai valori anomali. Pertanto, la correlazione dovrebbe essere usata solo come supplemento a un grafico di dispersione (dopo aver esaminato i dati).