Calcolatrice del flusso isentropico

Quando un gas viene forzato attraverso un tubo, le molecole di gas vengono deviate dalle pareti del tubo. Se la velocità del gas è molto inferiore alla velocità del suono del gas, la densità del gas rimane costante e la velocità del flusso aumenta. Considerando il flusso attraverso un tubo, come mostrato in figura, se il flusso viene compresso molto gradualmente (l’area diminuisce) e poi espanso gradualmente (l’area aumenta), le condizioni del flusso ritornano ai loro valori originali. Da una considerazione della seconda legge della termodinamica, un flusso reversibile mantiene un valore costante di entropia. Gli ingegneri chiamano questo tipo di flusso un flusso isentropico; una combinazione della parola greca “iso” (stesso) ed entropia.

I flussi isentropici si verificano quando il cambiamento nelle variabili di flusso è piccolo e graduale, come il flusso ideale attraverso thenozzleshown sopra. Se un flusso supersonico viene ruotato mentre l’area del flusso aumenta è anch’esso isentropico; lo chiamiamo espansione isentropica a causa dell’aumento dell’area; se un flusso supersonico viene ruotato bruscamente e l’area del flusso diminuisce, si generano onde d’urto e il flusso è irreversibile; le relazioni isentropiche non sono più valide e il flusso è governato dalle relazioni d’urto oblique o normali.

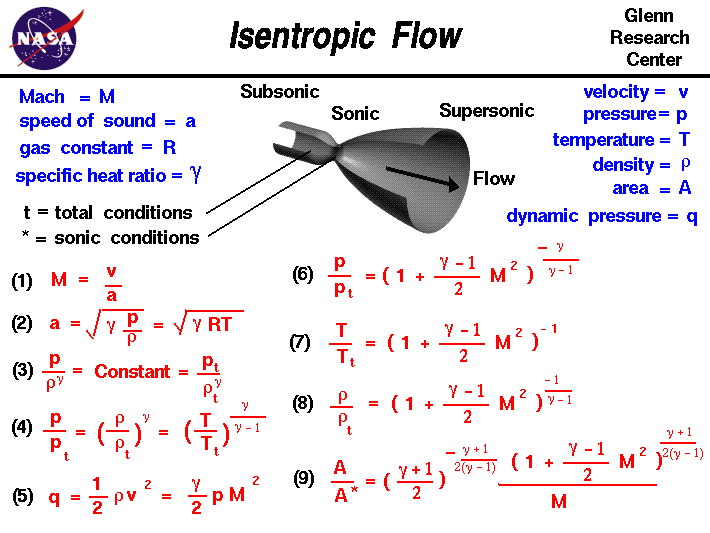
In questa slide abbiamo raccolto molte delle importanti equazioni che descrivono un flusso isentropico. Cominciamo con la definizione del numero di Mach, dato che questo parametro compare in molte delle equazioni del flusso isentropico. Il numero di Mach M è il rapporto tra la velocità del flusso v e la velocità del suono a.

Eq #1:

M = v / a

La velocità del suono, a sua volta, dipende dalla densità r, la pressione, p, la temperatura, T, e il rapporto dei calori specifici gam:

Eq #2:

a = sqrt(gam * p / r) = sqrt (gam * R * T)

dove R è la costante dei gas dalle equazioni di stato. Se cominciamo con le equazioni dell’entropia per un gas, si può dimostrare che la pressione e la densità di un flusso isentropico sono correlate come segue:

Eq #3:

p / r^gam = costante

Possiamo determinare il valore della costante definendo come condizioni totali la pressione e la densità quando il flusso è portato a riposo isentropico.Il pedice “t” usato in molte di queste equazioni sta per “condizioni totali”. (Probabilmente avete già qualche idea delle condizioni totali dall’esperienza con l’equazione di Bernoulli).

Eq #3:

p / r^gam = costante = pt / rt^gam

Utilizzando l’equazione di stato, possiamo ottenere facilmente le seguenti relazioni dall’equazione (3):

Eq #4:

p / pt = (r / rt)^gam = (T / Tt)^

La pressione dinamica q è definita come:

Eq #5:

q = (r * v^2) / 2 = (gam * p * M^2) / 2

Utilizzando la conservazione di massa, momento ed energia e la definizione di entalpia totale nel flusso, si generano le seguenti relazioni:

Eq #6:

p / pt = ^-

Eq #7:

T / Tt = ^-1

Eq #8:

r / rt = ^-

Poi considerando l’equazione del flusso di massa comprimibile.possiamo ricavare:

Eq #9:

A / A* = {^}*{^-} / M

Le condizioni stellate si verificano quando il flusso è strozzato e il numero di Mach è uguale a uno. Se il numero di Mach del flusso è determinato, tutte le altre relazioni di flusso possono essere determinate. Allo stesso modo, la determinazione di qualsiasi relazione di flusso (per esempio il rapporto di pressione) fisserà il numero di Mach e stabilirà tutte le altre condizioni di flusso.

Ecco un programma JavaScript che risolve le equazioni date in questa diapositiva.

Calcola