4.2: Momento magnetico e coppia

Momento di dipolo magnetico

Introduciamo qui una scorciatoia per i futuri calcoli di coppia. La quantità \(yz\) è l’area della spira, \(A\). Nelle applicazioni future, potremmo avere la corrente alimentata nella spira da un singolo filo, che è avvolto intorno al perimetro più volte. La forza esercitata su ogni lato della spira (e quindi la coppia) sarà quindi moltiplicata per il numero di giri del filo, \(N\). Il prodotto di \(N\), \(I\), e \(A\) è scritto come una singola quantità \(\mu\), dando la grandezza della coppia per questo caso la forma semplice di \(\tau = \mu B\).

Se questo anello gira sul suo asse, allora il braccio del momento si restringe. Per esempio, se la parte superiore della spira ruota indietro e la parte inferiore ruota in avanti di \(90^o\), allora le forze su quei segmenti saranno direttamente distanti tra loro. Queste forze agiscono direttamente attraverso l’asse, quindi la coppia che producono è zero. Sappiamo che la coppia e il campo magnetico sono entrambi vettori, e la coppia creata è legata all’orientamento della spira nel campo. Possiamo spiegare l’orientamento della spira definendo un momento di dipolo magnetico:

Il vettore \(\overrightarrow A\) ha una grandezza uguale all’area della spira, e ha una direzione che è perpendicolare al piano della spira, nella direzione definita come segue: Arricciate le dita della mano destra in una direzione che traccia la direzione della corrente attorno alla spira, e il pollice di quella mano indica la direzione del vettore. Per esempio, la spira in figura 4.2.1 avrebbe un momento magnetico che punta fuori dalla pagina.

Il vettore coppia può ora essere calcolato dal momento di dipolo magnetico nello stesso modo in cui si calcolava la coppia esercitata su un dipolo elettrico:

Si può vedere che questo funziona per il caso mostrato in figura 4.2.1: L’angolo tra il momento del dipolo magnetico (che punta fuori dalla pagina) e il campo magnetico è \(90^o\), quindi il seno dell’angolo tra questi vettori che appare nel prodotto incrociato è 1, dando la risposta che abbiamo trovato sopra. Quando la spira ruota intorno all’asse orizzontale, l’angolo tra il momento di dipolo magnetico e il campo cambia, riducendo i bracci di momento delle forze di un fattore di \(\sin\theta\) – esattamente la quantità considerata nel prodotto incrociato. Quando la spira ruota fino al punto in cui il suo piano è perpendicolare al campo, il momento magnetico e il campo sono paralleli, rendendo la coppia nulla, come abbiamo trovato sopra.

Anche se abbiamo derivato la formula per il momento di dipolo magnetico usando un rettangolo, si scopre che finché il loop giace in un piano, la formula funziona a prescindere dalla forma che ha. Come esempio illustrativo, risolveremo la coppia su un anello circolare. Questo è un esempio più difficile del rettangolo, per ragioni che diventeranno chiare, ma dimostra importanti strumenti per integrare contributi infinitesimali e trattare con prodotti vettoriali.

Figura 4.2.2a – Coppia su un anello circolare chiuso di filo in un campo magnetico uniforme

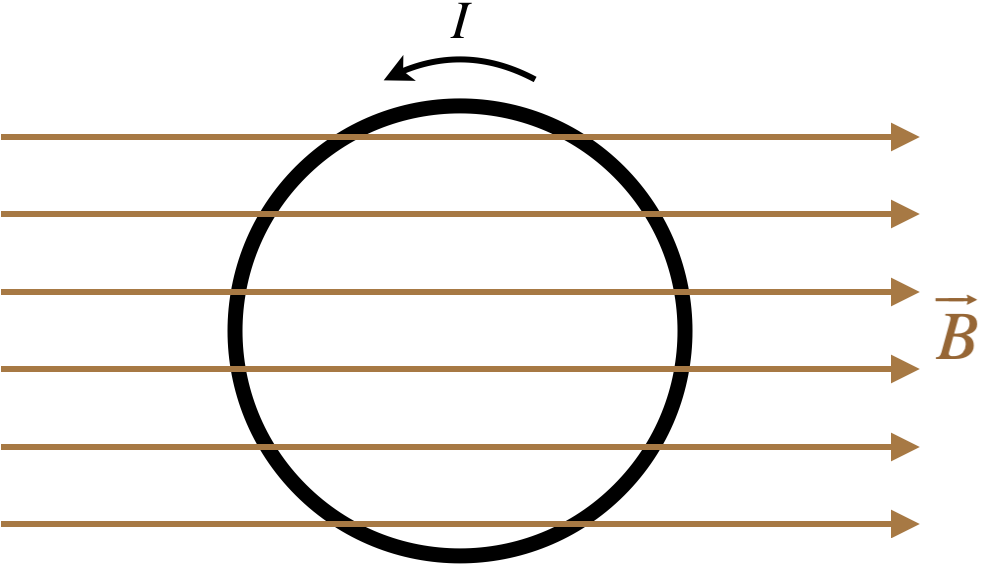
Come abbiamo fatto per l’integrazione delle distribuzioni di carica per ottenere i campi, iniziamo introducendo un sistema di coordinate (assicuriamoci che sia destrorso, cioè scegliamo gli assi in modo tale che la distribuzione della carica sia uguale a quella del campo.cioè scegliere gli assi in modo che \(\widehat i \volte \widehat j = \widehat k\)), selezionare un pezzo infinitesimale del loop, e descriverlo in termini di coordinate, etichettando qualsiasi variabile che avremo bisogno di conoscere lungo il percorso.

Figura 4.2.2b – Coppia su un anello circolare chiuso di filo in un campo magnetico uniforme

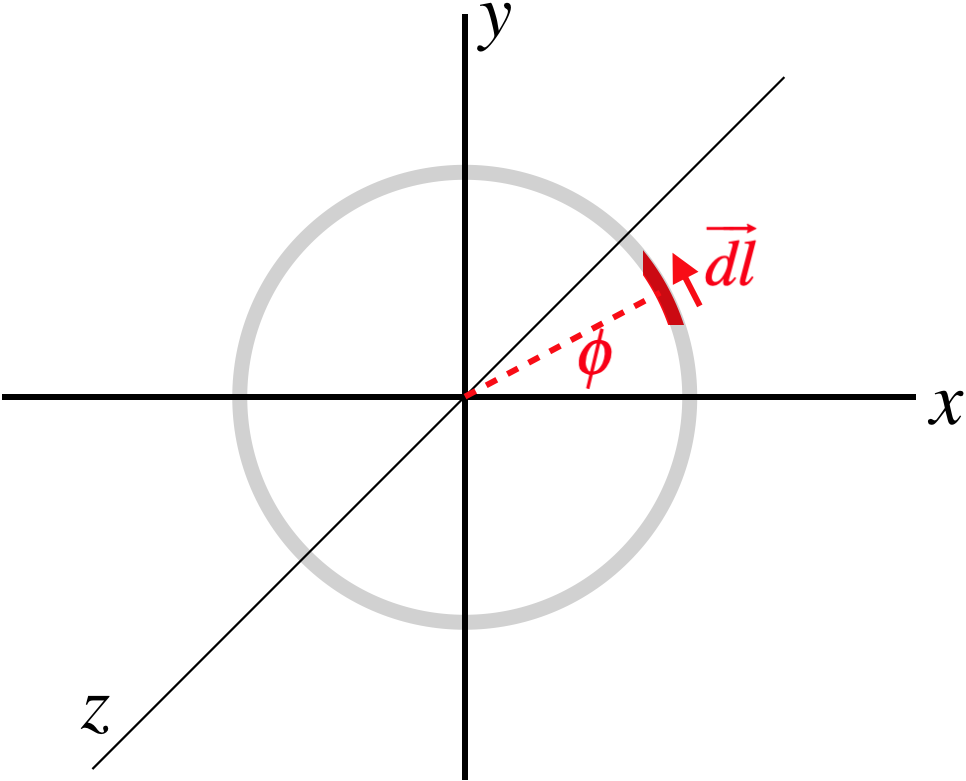
Qui abbiamo scelto di mettere l’anello nel piano \(x)-(y), e il campo magnetico punta nella direzione \(+x)-. Una fetta infinitesimale di filo è stata selezionata ad un angolo \(\phi\) dall’asse \(+x)-.

Poi dobbiamo esprimere matematicamente il vettore \(\overrightarrow {dl}\). La sua grandezza è la lunghezza di un segmento infinitesimale di arco, che è \(R\;d\phi\). La direzione è più complicata, ma ingrandendo l’immagine e facendo un po’ di geometria, possiamo determinare le sue componenti:

Figura 4.2.3 – Scrivere il vettore dell’elemento corrente

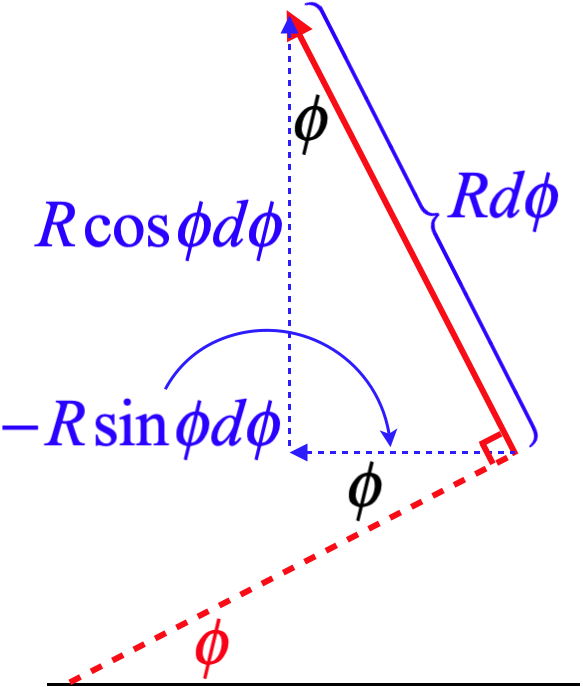
Mettendo tutto insieme in un unico vettore:

Abbiamo ora tutto quello che ci serve. Per quanto la geometria sia complicata con la forza e poi la coppia, non dobbiamo tenerne traccia – tutto quello che dobbiamo fare è fare la matematica vettoriale correttamente. Per esempio, la forza sull’elemento corrente è:

times\left]

Ricordando i prodotti incrociati dei vettori unitari da Fisica 9A, inseriamo \(\widehat i\times\widehat i = 0\) e \(\widehat j\times\widehat i = -\widehat k\), e la forza su questo elemento diventa:

Per ottenere la coppia, scegliamo l’origine come punto di riferimento, e calcoliamo direttamente il contributo infinitesimale alla coppia. Inserendo il vettore posizione e facendo la matematica vettoriale si ottiene:

Resta solo da sommare tutti i contributi di coppia, il che significa integrare l’angolo \(\phi\) da \(0\freccia 2\pi\):

= IR^2B\left=I\left(\pi R^2\right)B\;\widehat j\]

Certo, la grandezza della coppia risulta essere \(\mu\;B\), dove \(\mu=IA\). E usando la regola della mano destra per ottenere la direzione del momento magnetico (fuori dalla pagina) seguita dalla direzione della coppia dalla regola della mano destra applicata a \(\overrightarrow\mu\times\overrightarrow B\), conferma che anche la direzione funziona.

Questo problema sembrava molto scoraggiante perché la direzione di \(\overrightarrow {dl}\ è cambiata ovunque sul cerchio, ma una volta che questo vettore è scritto in termini di \(\phi\) e i vettori unitari, la matematica fa il resto!