17.2 Conduzione e convezione combinate

Avanti: 17.3 Numeri senza dimensione e Up: 17. Trasferimento di calore convettivo Previous: 17.1 L’analogia di Reynolds Contents Index

Possiamo ora analizzare problemi in cui si verificano sia la conduzione che la convezione, iniziando con una parete raffreddata da un fluido che scorre su ogni lato. Come discusso, una descrizione del trasferimento di calore convettivo può essere data esplicitamente come

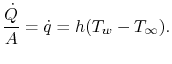
$\displaystyle \frac{dot{Q}{A}={dot{q} = h(T_w-T_\infty).$

Questo potrebbe rappresentare un modello di una pala di turbina con raffreddamento interno. La figura 17.6 mostra la configurazione.

Figura 17.6:Parete conduttrice con trasferimento di calore convettivo

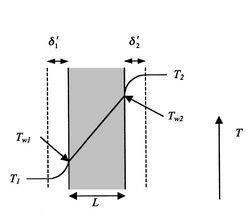
Il trasferimento di calore nel fluido 1 è dato da

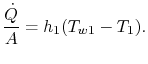
$\displaystyle \frac{\dot{Q}{A} = h_1(T_{w1}-T_1).$

che è il trasferimento di calore per unità di superficie al fluido. Il trasferimento di calore nel fluido 2 è analogamente dato da

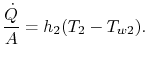
$\displaystyle \frac{dot{Q}{A} = h_2 (T_2 -T_{w2}).$

Al di là del muro, abbiamo

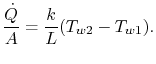
$\displaystyle \frac{\dot{Q}{A} = \frac{k}{L}(T_{w2} -T_{w1}).$

La quantità $\frac{Q}/A$ è la stessa in tutte queste espressioni. Mettendole tutte insieme per scrivere la caduta di temperatura complessiva nota, si ottiene una relazione tra il trasferimento di calore e la caduta di temperatura complessiva, :

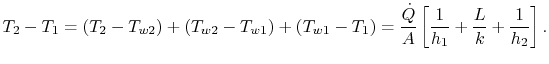$\displaystyle T_2-T_1 = (T_2-T_{w2})+(T_{w2}-T_{w1})+(T_{w1}-T_1) =\frac{\dot{Q}{A}\left.$

(17..20)

Possiamo definire una resistenza termica, , come in precedenza, in modo tale che

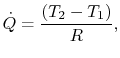
$\displaystyle \dot{Q} =\frac{(T_2 -T_1)}{R},$

dove è dato da

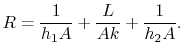$displaystyle R = \frac{1}{h_1A} + \frac{L}{Ak} + \frac{1}{h_2A}.$

(17..21)

L’equazione (17.21) è la resistenza termica per una parete solida con trasferimento di calore per convezione su ogni lato.

Per una pala di turbina in un motore a turbina a gas, il raffreddamento è una considerazione critica. In termini di Figura 17.6, è la temperatura all’uscita del combustore (ingresso della turbina) e è la temperatura all’uscita del compressore. Vogliamo trovare $T_{w2}$ perché questa è la più alta temperatura del metallo. Da(17.20), la temperatura di parete può essere scritta come

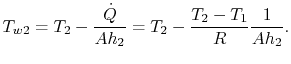$\displaystyle T_{w2} = T_2 - \frac{\dot{Q}}{Ah_2}= T_2 - \frac{T_2 - T_1}{R}\frac{1}{Ah_2}.$

(17..22)

Utilizzando l’espressione per la resistenza termica, le temperature della parete possono essere espresse in termini di coefficienti di trasferimento di calore e proprietà della parete come

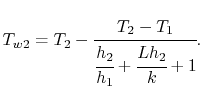$\displaystyle T_{w2} = T_2 - \cfrac{T_2 - T_1}{\cfrac{h_2}{h_1}+\cfrac{Lh_2}{k}+1}.$

(17..23)

L’equazione (17.23) fornisce alcune linee guida di progettazione di base. L’obiettivo è di avere un basso valore di $T_{w2}$ . Questo significa che dovrebbe essere grande, dovrebbe essere grande (ma potremmo non avere molta flessibilità nella scelta del materiale) e dovrebbe essere piccolo. Un modo per ottenere il primo di questi è quello di avere basso (per esempio, per far uscire l’aria di raffreddamento come inFigura 17.1 per schermare la superficie).

Un secondo esempio di conduzione e convezione combinate è dato da un cilindro esposto a un fluido che scorre. La geometria è mostrata inFigura 17.7.

Figura 17.7:Cilindro in un fluido che scorre

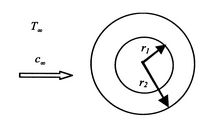
Per il cilindro il flusso di calore alla superficie esterna è dato da

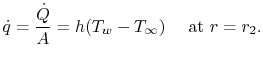
$\displaystyle \dot{q} = \frac{dot{Q}}{A} = h(T_w-T_infty)\quadro \textrm{ a}r=r_2.$

La condizione limite alla superficie interna potrebbe essere sia una condizione di flusso di calore che una specificazione di temperatura; usiamo quest’ultima per semplificare l’algebra. Così, a . Questo è un modello per il trasferimento di calore in un tubo di raggio circondato da un isolamento di spessore . La soluzione per una regione cilindrica è stata data nella Sezione 16.5.1 come

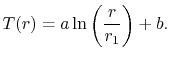
$\displaystyle T(r) =a\ln\left(\frac{r}{r_1}}right) +b.$

Usando la condizione limite si ottiene .

All’interfaccia tra il cilindro e il fluido, , la temperatura e il flusso termico sono continui. (Domanda: perché è così? Come argomenteresti il punto?)

$displaystyle \dot{q} = \sottobraccio{-k\frac{dT}{dr}}_{sottostack{\textrm{ calore fl......2}{r_1}\destra)+T_1\destra)-T_\infty\destra]} _\textrm{flusso di calore superficiale al fluido}$

(17..24)

Infilando la forma della distribuzione della temperatura nel cilindro nell’equazione (17.24) yields

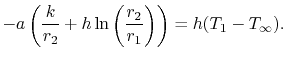
$\displaystyle -a\left(\frac{k}{r_2}+h\ln\left(\frac{r_2}{r_1}\right)\right)=h(T_1-T_\infty).$

La costante di integrazione, , è

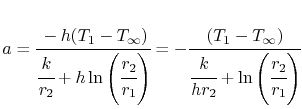
$displaystyle a=\cfrac{-h(T_1-T_\infty)}{\cfrac{k}{r_2}+h\ln\left(\cfrac{r_2}{r......t)}=-\cfrac{(T_1-T_\infty)}{\cfrac{k}{hr_2}+lnn\left(\cfrac{r_2}{r_1}}destra)}$

e l’espressione per la temperatura è, in forma normalizzata-non-dimensionale,

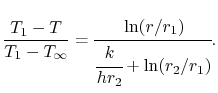$\displaystyle \frac{T_1-T}{T_1-T_infty} = \cfrac{\ln(r/r_1)}{\cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..25)

Il flusso di calore per unità di lunghezza, $\dot{Q}$ , è dato da

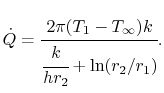$\displaystyle \dot{Q}=\cfrac{2\pi(T_1-T_infty)k}{\cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..26)

Le unità nell’equazione (17.26) sono W/m-s.

Un problema di interesse è la scelta dello spessore dell’isolante per minimizzare la perdita di calore per una differenza di temperatura fissa $T_1-T_\infty$ tra l’interno del tubo e il fluido che scorre lontano dal tubo. ( $T_1-T_\infty$ è la distribuzione della temperatura che guida il tubo). Per capire il comportamento del trasferimento di calore esaminiamo il denominatore nell’equazione (17.26) al variare di . Lo spessore dell’isolamento che dà il massimo trasferimento di calore è dato da

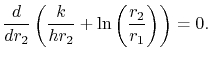$\displaystyle \frac{d}{dr_2}\left(\frac{k}{hr_2}+\ln\left(\frac{r_2}{r_1}\right)\right)=0.$

(17..27)

(Domanda: come sappiamo che questo è un massimo?)

Dall’equazione (17.27), il valore di per il massimo $\dot{Q}$ è così

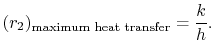$displaystyle (r_2)_{\textrm{massimo trasferimento di calore}} = \frac{k}{h}.$

(17..28)

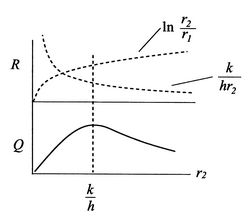
Se è inferiore a questo, possiamo aggiungere isolamento e aumentare la perdita di calore. Per capire perché questo accade, consideriamo la figura 17.8, che mostra un’aschematizzazione della resistenza termica e del trasferimento di calore. Quando aumenta da un valore inferiore a , si verificano due effetti. In primo luogo, lo spessore dell’isolamento aumenta, tendendo a diminuire il trasferimento di calore perché il gradiente di temperatura diminuisce; in secondo luogo, l’area della superficie esterna dell’isolamento aumenta, tendendo ad aumentare il trasferimento di calore. Il secondo è (vagamente) associato al termine , il primo al termine $\ln(r_2/r_1)$ . Ci sono quindi due effetti concorrenti che si combinano per dare un massimo $\dot{Q}$ a .