Hoe sterk is 256-bit encryptie?

“Er staat 256-bit encryptiesterkte… is dat goed?”

De meeste mensen zien de term 256-bit encryptie de hele tijd vallen en hebben – als we eerlijk zijn – absoluut geen idee wat het betekent of hoe sterk het is. Als je eenmaal verder gaat dan het oppervlakkige “het vervormt gegevens en maakt ze onleesbaar”, is encryptie een ongelooflijk ingewikkeld onderwerp. Het is geen lichte lectuur. De meesten van ons hebben geen boek over modulaire exponentiatie op het nachtkastje naast hun bed liggen.

Daarom is het begrijpelijk dat er enige verwarring is als het gaat om encryptie, wat het betekent, wat “goed” is, enz. Er is geen gebrek aan vragen over encryptie – in het bijzonder 256-bits encryptie.

De belangrijkste vraag is: Hoe sterk is 256-bit encryptie?

Daar gaan we het vandaag over hebben. We bespreken wat een beetje beveiliging eigenlijk is, we gaan in op de meest voorkomende vorm van 256-bits versleuteling en we bespreken wat er voor nodig is om versleuteling van die sterkte te kraken.

Laten we het eens doornemen.

Een snelle opfrisser over encryptie, in het algemeen

Wanneer je iets versleutelt, neem je de onversleutelde gegevens, de zogenaamde klare tekst, en voert er een algoritmische functie op uit om een stukje versleutelde cijfertekst te maken. Het algoritme dat je gebruikt wordt de sleutel genoemd. Met uitzondering van openbare sleutels in asymmetrische encryptie, moet de waarde van de encryptiesleutel geheim worden gehouden. De prive-sleutel die bij dat stukje cijfertekst hoort, is de enige manier om het te ontcijferen.

Nou, dat klinkt allemaal erg abstract, dus laten we een voorbeeld gebruiken. En we laten Bob en Alice erbuiten, want die hebben het druk met het uitleggen van encryptie in letterlijk elk ander voorbeeld op het internet.

Laten we Jack en Diane nemen, en laten we zeggen dat Jack Diane een bericht wil sturen dat zegt: “Oh ja, het leven gaat door.”

Jack neemt zijn bericht en gebruikt een algoritme of versleuteling – de encryptiesleutel – om het bericht te vervormen tot versleutelde tekst. Nu geeft hij het door aan Diane, samen met de sleutel, die gebruikt kan worden om het bericht te ontcijferen, zodat het weer leesbaar is.

Zolang niemand anders de sleutel in handen krijgt, is de cijfertekst waardeloos omdat hij niet kan worden gelezen.

Hoe werkt moderne encryptie?

Jack en Diane hebben zojuist de meest elementaire vorm van encryptie gedemonstreerd. En terwijl de wiskunde die in primitieve cijfers werd gebruikt tamelijk eenvoudig was – omdat het door een mens moest worden uitgevoerd – heeft de komst van computers de complexiteit van de wiskunde die aan moderne cryptosystemen ten grondslag ligt, vergroot. Maar de concepten zijn nog steeds grotendeels hetzelfde.

Een sleutel, of specifiek algoritme, wordt gebruikt om de gegevens te versleutelen, en alleen een andere partij met kennis van de bijbehorende privésleutel kan de versleuteling ongedaan maken.

In dit voorbeeld, in plaats van een geschreven boodschap waarin somber wordt verkondigd dat het leven doorgaat zelfs nadat de vreugde verloren is gegaan, doen Jack en Diane ‘hun best’ op computers (nog steeds ‘vasthoudend aan 16’ – sorry, dit zijn John Mellencamp-grapjes die buiten de VS waarschijnlijk geen steek houden). De encryptie die nu gaat plaatsvinden is digitaal.

De computer van Jack gebruikt zijn sleutel, die in werkelijkheid een uiterst ingewikkeld algoritme is dat is afgeleid van gegevens die zijn gedeeld door de apparaten van Jack en Diane, om de onbewerkte tekst te versleutelen. Diane gebruikt haar bijbehorende symmetrische sleutel om de data te ontsleutelen en te lezen.

Maar wat wordt er eigenlijk versleuteld? Hoe versleutel je “gegevens?”

In het oorspronkelijke voorbeeld waren het echte letters op een stuk papier die in iets anders werden veranderd. Maar hoe codeert een computer gegevens?

Dat gaat terug op de manier waarop computers feitelijk met gegevens omgaan. Computers slaan informatie op in binaire vorm. 1’s en 0’s. Alle gegevens die in een computer worden ingevoerd, worden gecodeerd zodat ze leesbaar zijn voor de machine. Het zijn die gecodeerde gegevens, in hun ruwe vorm, die gecodeerd worden. Dit is een onderdeel van de verschillende bestandstypen die door SSL/TLS-certificaten worden gebruikt, en hangt gedeeltelijk af van het type coderingsschema dat je probeert te versleutelen.

Dus Jack’s computer codeert de gecodeerde gegevens en stuurt ze naar Diane’s computer, die de bijbehorende privésleutel gebruikt om de gegevens te decoderen en te lezen.

Zolang de privésleutel, je weet wel… privésleutel blijft, blijft de versleuteling veilig.

De moderne versleuteling heeft het grootste historische obstakel voor versleuteling opgelost: sleuteluitwisseling. Vroeger moest de privé-sleutel fysiek worden doorgegeven. Sleutelbeveiliging was letterlijk een kwestie van het fysiek opslaan van de sleutel op een veilige plaats. Het compromitteren van sleutels maakte de encryptie niet alleen onbetrouwbaar, het kon je ook het leven kosten.

In de jaren 70 begon een trio cryptografen, Ralph Merkle,Whitfield Diffie en Martin Hellman, te werken aan een manier om veilig een encryptie sleutel te delen op een onbeveiligd netwerk terwijl een aanvaller toekeek. Zij slaagden daarin op theoretisch niveau, maar waren niet in staat een asymmetrische versleutelingsfunctie te bedenken die praktisch was. Ze hadden ook geen mechanisme voor authenticatie (maar dat is een heel ander gesprek). Merkle kwam met het eerste concept, maar zijn naam is niet verbonden aan het sleuteluitwisselingsprotocol dat zij uitvonden – ondanks de protesten van de andere twee bedenkers.

Rongeveer een jaar later creëerden Ron Rivest, Adi Shamir en Leonard Adleman een gelijknamige methode voor sleuteluitwisseling, gebaseerd op Diffie-Hellman sleuteluitwisseling (RSA), een methode die ook versleuteling/ontsleuteling en authenticatiefuncties bevatte. Dit is relevant omdat het de geboorte was van een geheel nieuwe iteratie van encryptie: asymmetrische encryptie.

Zij hebben ons ook de eerder genoemde Bob en Alice gegeven, wat het voor mij in ieder geval een wassen neus maakt.

Hoe dan ook, het verschil tussen symmetrische en asymmetrische encryptie begrijpen is de sleutel tot de rest van deze discussie.

Asymmetrische encryptie vs. Symmetrische encryptie

Symmetrische encryptie wordt ook wel versleuteling met een privésleutel genoemd, omdat beide partijen een symmetrische sleutel moeten delen die kan worden gebruikt om gegevens zowel te versleutelen als te ontsleutelen.

Asymmetrische encryptie daarentegen wordt ook wel openbare-sleutel-encryptie genoemd. Een betere manier om aan asymmetrische encryptie te denken is het te zien als eenrichtingsencryptie.

In tegenstelling tot beide partijen die een privésleutel delen, is er een sleutelpaar. De ene partij bezit een openbare sleutel die kan versleutelen, de andere een particuliere sleutel die kan ontsleutelen.

Asymmetrische encryptie wordt voornamelijk gebruikt als mechanisme voor het uitwisselen van symmetrische privésleutels. Daar is een reden voor: asymmetrische encryptie is historisch gezien een duurdere functie vanwege de grootte van de sleutels. Dus publieke sleutel cryptografie wordt meer gebruikt als een externe muur om de partijen te helpen beschermen als ze een verbinding tot stand brengen, terwijl symmetrische encryptie wordt gebruikt binnen de eigenlijke verbinding zelf.

2048-bit sleutels vs 256-bit sleutels

In SSL/TLS, dient asymmetrische encryptie één, uiterst belangrijke functie. Het laat de client de gegevens coderen die door beide partijen worden gebruikt om de symmetrische sessiesleutels af te leiden die ze zullen gebruiken om te communiceren. Je zou asymmetrische encryptie nooit kunnen gebruiken om functioneel te communiceren. Hoewel de openbare sleutel kan worden gebruikt om een digitale handtekening te verifiëren, kan hij niets ontsleutelen dat met de privé-sleutel wordt versleuteld, vandaar dat we asymmetrische encryptie “eenrichtingsverkeer” noemen.

Maar het grootste probleem is dat de sleutelgrootte de eigenlijke versleutelings- en ontsleutelingsfuncties duur maakt in termen van CPU-resources die ze opslokken. Dit is de reden waarom veel grotere organisaties en ondernemingen, wanneer ze SSL/TLS op grote schaal implementeren, de handshakes offloaden: om resources op hun applicatieservers vrij te maken.

In plaats daarvan gebruiken we symmetrische encryptie voor de feitelijke communicatie die tijdens een versleutelde verbinding plaatsvindt. Symmetrische sleutels zijn kleiner en minder duur om mee te rekenen.

Dus, als je iemand een 2048-bit private key ziet noemen, bedoelt hij waarschijnlijk een RSA private key. Dat is een asymmetrische sleutel. Hij moet voldoende bestand zijn tegen aanvallen, omdat hij zo’n belangrijke functie vervult. Ook omdat sleuteluitwisseling de beste aanvalsvector is om een verbinding te compromitteren. Het is veel gemakkelijker om de gegevens te stelen die worden gebruikt om de symmetrische sessiesleutel te maken en die zelf te berekenen, dan om de sleutel te kraken met brute kracht nadat hij al in gebruik is.

Dat roept de vraag op: “Hoe sterk is 256-bit encryptie?” Als het minder sterk is dan een 2048-bit sleutel, is het dan nog steeds voldoende? En daar gaan we antwoord op geven, maar eerst moeten we wat verder gaan om de juiste context te schetsen.

Wat is precies een “bit” aan beveiliging?

Het is heel belangrijk dat we het hebben over veiligheidsbits en het vergelijken van de sterkte van encryptie tussen algoritmen voordat we in een praktische discussie terechtkomen over hoe sterk 256 bits eigenlijk is.

Een 128-bits AES-sleutel bijvoorbeeld, die de helft is van de huidige aanbevolen grootte, is ongeveer gelijk aan een 3072-bits RSA-sleutel in termen van de werkelijke veiligheid die ze bieden.

Het is ook belangrijk om het verschil te begrijpen tussen beveiligingsclaim en beveiligingsniveau.

• Veiligheidsclaim – Dit is het beveiligingsniveau dat de cryptografische primitieve – de codeer- of hashfunctie in kwestie – oorspronkelijk was ontworpen om te bereiken.
• Beveiligingsniveau – De daadwerkelijke sterkte die de cryptografische primitieve bereikt.

Dit wordt meestal uitgedrukt in bits. Een bit is een basiseenheid van informatie. Het is eigenlijk een portmanteau van “binair cijfer,” wat zowel ongelooflijk efficiënt is als ook niet zo efficiënt. Natuurlijk, het is makkelijker om bit te zeggen. Maar ik heb net een hele alinea besteed om uit te leggen dat een bit in feite een 1 of een 0 is in binair, terwijl de oorspronkelijke term dat met twee woorden zou hebben bereikt. Dus, jij beslist of het efficiënter is. Hoe dan ook, we gaan niet veel meer tijd aan binair besteden dan we al hebben gedaan, maar Ross heeft er een paar maanden geleden een geweldig artikel over geschreven dat je eens moet lezen.

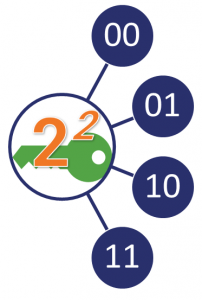
Hoe dan ook, beveiligingsniveau en beveiligingsclaim worden doorgaans uitgedrukt in bits. In deze context verwijst het aantal bits (n) naar het aantal bewerkingen dat een aanvaller hypothetisch gezien zou moeten uitvoeren om de waarde van de private sleutel te raden. Hoe groter de sleutel, hoe moeilijker het is om hem te raden/kraken. Onthoud dat deze sleutel bestaat uit 1-en en 0-en, dus er zijn twee mogelijke waarden voor elk bit. De aanvaller zou 2n operaties moeten uitvoeren om de sleutel te kraken.

Dat is misschien een beetje te abstract, dus hier is een snel voorbeeld: Laten we zeggen dat er een 2-bit sleutel is. Dat betekent dat die 22 (4) waarden zal hebben.

Dat zou voor een computer triviaal eenvoudig te kraken zijn, maar als je aan grotere sleutels begint, wordt het voor een moderne computer onbetaalbaar moeilijk om de waarde van een private sleutel in een redelijke hoeveelheid tijd te raden.

Maar voordat we gaan rekenen, nog even terug naar beveiligingsclaim vs. beveiligingsniveau

Beveiligingsclaim vs. beveiligingsniveau

Typisch is dat als je encryptie op de markt ziet, er wordt geadverteerd met de beveiligingsclaim. Dat is wat het beveiligingsniveau onder optimale omstandigheden zou zijn. We gaan dit specifiek houden voor SSL/TLS en PKI, maar het percentage van de tijd dat de optimale omstandigheden aanwezig zijn is verre van 100%. Misconfiguraties zijn aan de orde van de dag, evenals het handhaven van ondersteuning voor oudere versies van SSL/TLS en verouderde cipher suites omwille van interoperabiliteit.

In de context van SSL/TLS vindt, wanneer een client op een website aankomt, een handshake plaats waarbij de twee partijen een wederzijds overeengekomen cipher suite bepalen om te gebruiken. De feitelijke versleutelingssterkte hangt af van de parameters die tijdens de handshake worden vastgesteld, alsmede van de mogelijkheden van de server en de client zelf.

Soms biedt 256-bit encryptie slechts een beveiligingsniveau van 128 bits. Dit komt vooral voor bij hashing-algoritmen, die de weerstand tegen twee verschillende soorten aanvallen meten:

• Botsingen – Als twee verschillende stukjes gegevens dezelfde hash-waarde opleveren, heet dat een botsing en dat breekt het algoritme.
• PreImage resistance – Hoe resistent een algoritme is tegen een exploit waarbij een aanvaller een bericht met een specifieke hashwaarde probeert te vinden.

Zo heeft SHA-256 bijvoorbeeld een collision resistance van 128 bits (n/2) , maar een PreImage resistance van 256 bits. Het is duidelijk dat hashing anders is dan encryptie, maar er zijn ook genoeg overeenkomsten die het vermelden waard maken.

En hoe sterk is 256-bits encryptie?

Opnieuw varieert dit afhankelijk van het algoritme dat u gebruikt, en het varieert van asymmetrische tot symmetrische encryptie. Zoals we al zeiden, dit zijn geen 1:1 vergelijkingen. In feite is het beveiligingsniveau van asymmetrische encryptie niet zo wetenschappelijk als het misschien lijkt te zijn. Asymmetrische encryptie is gebaseerd op wiskundige problemen die gemakkelijk in één richting uit te voeren zijn (encryptie) maar buitengewoon moeilijk om te keren (decryptie). Daarom zijn aanvallen op asymmetrische cryptosystemen met een openbare sleutel doorgaans veel sneller dan de brute kracht-achtige zoektochten naar sleutelruimte die symmetrische encryptiesystemen met een privé-sleutel teisteren. Als je het hebt over het veiligheidsniveau van cryptografie met een openbare sleutel, gaat het dus niet om een vast cijfer, maar om een berekening van de computationele hardheid van de implementatie tegen de beste, momenteel meest bekende aanval.

Symmetrische encryptiesterkte is iets eenvoudiger te berekenen vanwege de aard van de aanvallen waartegen ze moeten worden verdedigd.

Dus laten we eens kijken naar AES of Advanced Encryption Standard, dat vaak wordt gebruikt als bulkcijfer met SSL/TLS. Bulk ciphers zijn de symmetrische cryptosystemen die feitelijk de communicatie beveiligen die plaatsvindt tijdens een versleutelde HTTPS-verbinding.

Er zijn historisch gezien twee smaken: blokcijfers en stroomcijfers.

Blokcijfers splitsen alles wat ze versleutelen op in blokken ter grootte van een sleutel en versleutelen deze. Bij het ontcijferen moeten de blokken weer in elkaar worden gezet. En als het bericht te kort of te lang is, wat meestal het geval is, moeten ze worden opgedeeld en/of opgevuld met wegwerpgegevens om ze de juiste lengte te geven. Padding aanvallen zijn een van de meest voorkomende bedreigingen voor SSL/TLS.

TLS 1.3 heeft deze manier van bulk encryptie om precies die reden afgeschaft, nu moeten alle cijfers op stream mode worden gezet. Stream cijfers versleutelen gegevens in pseudorandom stromen van elke lengte, ze worden beschouwd als eenvoudiger te implementeren en vereisen minder middelen. TLS 1.3 heeft ook een aantal onveilige stream-ciphers afgeschaft, zoals RC4.

Dus, om een lang verhaal kort te maken, er zijn tegenwoordig nog maar twee bulkciphers, AES en ChaCha20. We gaan ons nu op AES richten, want ChaCha20 is een heel ander verhaal.

GCM staat voor Galois Counter Mode, waarmee AES – dat eigenlijk een blokcijfer is – in stream-modus kan werken. CCM is vergelijkbaar, het combineert een teller mode met een bericht authenticatie functies.

Zoals we hebben besproken, kun je AES veilig draaien in GCM of CCM met 128-bit sleutels en dat gaat prima. Je krijgt dan het equivalent van 3072-bit RSA in termen van het beveiligingsniveau. Maar we raden meestal aan om 256-bits sleutels te gebruiken, zodat je de maximale rekenhardheid behoudt voor een zo lang mogelijke periode.

Dus, laten we eens kijken naar die 256-bits sleutels. Een 256-bit sleutel kan 2566 mogelijke combinaties hebben. Zoals we al eerder hebben gezegd, zou een twee-bits sleutel vier mogelijke combinaties hebben (en gemakkelijk te kraken zijn door een twee-bits sleutel). We hebben hier echter te maken met exponentiëren, dus elke keer dat je de exponent, n, verhoogt, vergroot je het aantal mogelijke combinaties enorm. 2256 is 2 x 2, x 2, x 2… 256 keer.

Zoals we hebben besproken, is de beste manier om een versleutelingscode te kraken ‘brute-forcing’, wat in feite gewoon trial & error in eenvoudige bewoordingen is. Dus, als de sleutellengte 256-bit is, zijn er 2256 mogelijke combinaties, en een hacker moet de meeste van de 2256 mogelijke combinaties proberen voordat hij tot de conclusie komt. Het is waarschijnlijk niet nodig om ze allemaal te proberen om de sleutel te raden – meestal is dat ongeveer 50% – maar de tijd die nodig is om dit te doen zou veel langer duren dan een mensenleven.

Een 256-bit privé sleutel heeft 115.792.089.237.316.195.423.570.985.008.687.907.853.269.
984.665.640.564.039.457.584.007.913.129.639.936 (dat zijn 78 cijfers) mogelijke combinaties. Geen enkele supercomputer ter wereld kan dat binnen een redelijke tijd kraken.

Zelfs als je Tianhe-2 (MilkyWay-2) gebruikt, de snelste supercomputer ter wereld, kost het miljoenen jaren om 256-bit AES-encryptie te kraken.

Dat cijfer schiet nog omhoog als je probeert uit te rekenen hoeveel tijd het zou kosten om een RSA-privésleutel te kraken. Een 2048-bits RSA-sleutel zou volgens DigiCert 6,4 quadriljoen jaar (6.400.000.000.000.000.000 jaar) kosten om te berekenen.

Zoveel tijd heeft niemand.

Quantum Computing gaat dit allemaal veranderen

Nu zou eigenlijk een goede plek zijn om het een beetje te hebben over quantum encryptie en de bedreiging die het vormt voor onze moderne cryptografische primitieven. Zoals we net hebben besproken, werken computers binair. 1’s en 0’s. En de manier waarop bits werken op moderne computers is dat ze een bekende waarde moeten hebben, ze zijn of een 1 of een 0. Punt uit. Dat betekent dat een moderne computer maar één keer per keer kan raden.

Het is duidelijk dat dit het aantal bruteforce-combinaties in een poging om een privésleutel te kraken aanzienlijk beperkt.

Kwantumcomputers zullen dergelijke beperkingen niet kennen. Nu, twee dingen, ten eerste is quantum computing nog zo’n 7-10 jaar verwijderd van levensvatbaarheid, dus we zijn er nog lang niet. Sommige CA’s, zoals DigiCert, zijn begonnen met het plaatsen van post-kwantum digitale certificaten op IoT-apparaten die een lange levensduur zullen hebben om te proberen ze preventief te beveiligen tegen kwantumcomputing, maar verder zijn we nog steeds in de onderzoeksfase als het gaat om kwantum-proof encryptie.

Het probleem is dat kwantumcomputers geen bits gebruiken, maar kwantumbits of qubits. Een kwantumbit kan BEIDE een 1 en een 0 zijn dankzij een principe dat superpositie wordt genoemd, wat iets ingewikkelder is dan we vandaag gaan doen. Qubits geven kwantumcomputers de kracht om hun brute kracht aanvallen te exponentiëren, wat effectief de computationele hardheid tenietdoet van de exponentiatie die plaatsvond met de cryptografische primitieve. Een vier Qubit computer kan effectief in vier verschillende posities (22) tegelijk zijn. Het is weer 2n, dus een Quantum Computer met n qubits kan 2n combinaties tegelijk proberen. Bristlecone, die 72 qubits heeft, kan 272 (4.722.366.482.869.645.213.696) waarden tegelijk uitproberen.

Alweer, we zijn daar nog ver van verwijderd en de quantumcomputer zou moeten uitvinden hoe hij het algoritme van Shor met succes kan uitvoeren, een ander onderwerp voor een andere dag, dus dit is nog steeds grotendeels theoretisch.

Toch lijkt 4,6 quadriljoen jaar ineens niet meer zo lang.

Laten we dit afronden…

256-bit encryptie is anno 2019 redelijk standaard, maar elke vermelding van 256-bit encryptie verwijst niet naar hetzelfde. Soms stijgt256-bits encryptie slechts tot een beveiligingsniveau van 128 bits. Soms zijn sleutelgrootte en beveiligingsniveau intrinsiek met elkaar verbonden, terwijl andere keren het ene slechts wordt gebruikt om het andere te benaderen.

Dus het antwoord op de vraag “hoe sterk is 256-bits encryptie” is er niet een met een eenduidig antwoord.

In de context van SSL/TLS gaat het echter meestal om AES-encryptie, waarbij 256 bits ook echt 256 bits betekent. En die 256-bits versleuteling is, voorlopig althans, nog steeds voldoende sterk.

Tegen de tijd dat een aanvaller met een moderne computer een 256-bit symmetrische sleutel kan kraken, is die niet alleen weggegooid, maar heeft u waarschijnlijk ook het SSL/TLS-certificaat vervangen waarmee die sleutel is gegenereerd.

Lang verhaal kort, de grootste bedreiging voor uw encryptie en uw encryptiesleutels is nog steeds wanbeheer, de technologie erachter is goed.