Lignes parallèles
Des lignes sont parallèles si elles sont toujours à la même distance (dite « équidistante »), et ne se rencontreront jamais. Rappelez-vous :
Toujours à la même distance et ne se touchant jamais.
La ligne rouge est parallèle à la ligne bleue dans chacun de ces exemples :
 |
 |
|
|
Exemple 1
|
Exemple 2
|
Les lignes parallèles pointent également dans la même direction.
Essayez vous-même :
Paires d’angles
Lorsque des lignes parallèles sont traversées par une autre ligne (que l’on appelle une Transversale), vous pouvez constater que de nombreux angles sont identiques, comme dans cet exemple :
Ces angles peuvent être transformés en paires d’angles qui ont des noms spéciaux.
Cliquez sur chaque nom pour le voir mis en évidence :
Maintenant jouez avec ici. Essayez de faire glisser les points, et de choisir différents types d’angles. Vous pouvez également désactiver ou activer « Parallèle »:
Tester les lignes parallèles
Certaines de ces paires d’angles spéciales peuvent être utilisées pour tester si les lignes sont vraiment parallèles :
|
 |
|||||||||||||||||||
Exemples
| Ces lignes sont parallèles, car une paire d’angles correspondants sont égaux. | 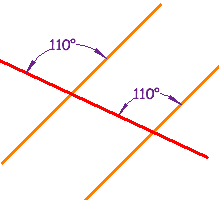 |
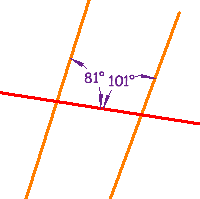 |
Ces lignes ne sont pas parallèles, car une paire d’angles intérieurs consécutifs ne fait pas 180° (81° + 101° =182°) | Ces lignes sont parallèles, car une paire d’angles intérieurs alternatifs est égale | 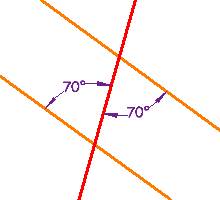 |
.
