Concepts en statistique

Propriétés de r

Nous allons maintenant discuter et illustrer plusieurs propriétés importantes du coefficient de corrélation en tant que mesure numérique de la force d’une relation linéaire.

1. La corrélation ne change pas lorsque les unités de mesure de l’une ou l’autre des variables changent. En d’autres termes, si nous changeons les unités de mesure de la variable explicative et/ou de la variable réponse, cela n’a aucun effet sur la corrélation (r).

Pour illustrer, comparez les deux versions du nuage de points de la relation entre l’âge d’un conducteur et la distance maximale pour lire un panneau d’autoroute.

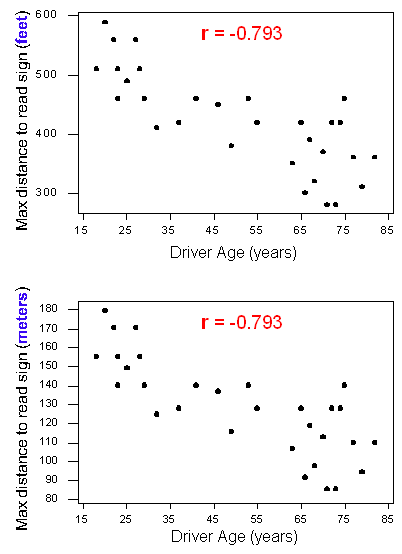
Le nuage de points du haut affiche les données originales où les distances maximales sont mesurées en pieds. Le nuage de points du bas affiche la même relation, mais avec des distances maximales changées en mètres. Remarquez que les valeurs y ont changé, mais que les corrélations sont les mêmes. Cet exemple montre qu’un changement d’unités ne modifie pas r. Cela est vrai même si nous changeons les unités des deux variables. C’est logique car un changement d’unités ne modifie pas le modèle des données. La direction, la forme et la force de la relation restent les mêmes. Comme r mesure la direction et la force d’une relation linéaire, la valeur de r reste la même.

2. La corrélation mesure uniquement la force d’une relation linéaire entre deux variables. Elle ignore tout autre type de relation, quelle que soit sa force. Par exemple, considérez la relation entre la consommation moyenne de carburant pour parcourir une distance fixe en voiture et la vitesse à laquelle la voiture roule :

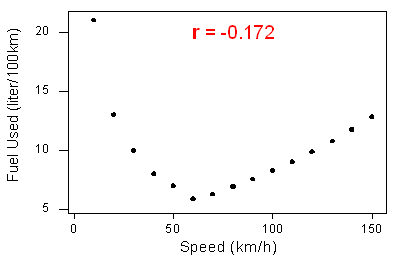
Les données ont une forme curviligne lisse. La relation est très forte car les données suivent parfaitement la courbe.

Notez que la corrélation r = -0,172 indique une faible relation linéaire. Cela est logique car les données ne suivent pas étroitement une forme linéaire. Ainsi, le coefficient de corrélation ne donne que des informations sur la force d’une relation linéaire. Il ne donne pas d’informations fiables sur la force d’une relation curviligne.

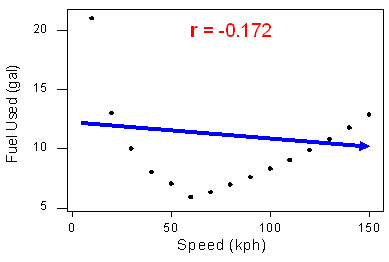
Cet exemple illustre que le coefficient de corrélation est inutile comme mesure de la force si la relation n’est pas linéaire. Il illustre également une règle importante : Toujours faire un nuage de points des données avant de calculer et d’interpréter la signification de r.

Pourquoi devrions-nous faire un nuage de points en premier ? Si nous ne regardions pas le nuage de points, mais uniquement r, quelle erreur pourrions-nous commettre ? Nous pourrions conclure que la relation entre les variables est faible (ou qu’il n’y a pas de relation) parce que r est proche de zéro. Mais cette conclusion est fausse. Nous avons mal interprété « r proche de 0 » comme un indicateur d’une relation faible ou d’une absence de relation plutôt que d’une relation linéaire faible ou d’une absence de relation linéaire. Nous pouvons facilement éviter cette mauvaise interprétation de r en regardant le nuage de points.

Résumons. Si r est proche de zéro, cela signifie que les données ont une relation linéaire très faible ou aucune relation linéaire. Lorsque r est proche de zéro, il est possible que les données aient une relation curviligne forte (comme nous l’avons vu dans cet exemple). Pour éviter les erreurs, nous devons regarder la forme des données dans le nuage de points avant de calculer et d’interpréter r. Si la forme n’est pas linéaire, n’utilisez pas r.

3. La corrélation en elle-même ne suffit pas à déterminer si une relation est linéaire. Pour le voir, examinons une situation avec une valeur r proche de 1 mais une relation qui n’est pas linéaire. Rappelez-vous l’étude dans laquelle les participants étaient payés pour répondre à une enquête. L’étude a examiné la relation entre le montant de l’incitation monétaire et le pourcentage de l’échantillon qui a renvoyé le sondage.

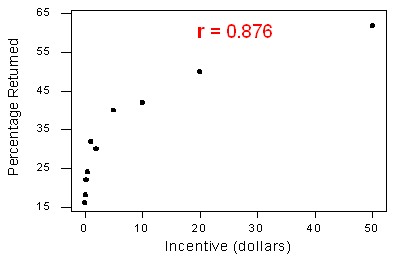
Les variables ont une forte relation curviligne, pourtant la corrélation est r = 0.876, assez proche de 1.

En revoyant les deux derniers exemples, nous voyons que les relations curvilignes fortes peuvent avoir une corrélation proche de 0 ou proche de 1. Donc la corrélation seule ne nous dit pas si une relation est linéaire. Nous devons regarder un nuage de points des données.

Toujours regarder les données !

4. La corrélation est fortement influencée par les valeurs aberrantes. Comme vous l’apprendrez dans les deux prochaines activités, la façon dont la valeur aberrante influence la corrélation dépend de la cohérence ou non de cette valeur avec le modèle de la relation linéaire.

À l’aide de la simulation ci-dessous, explorons comment une valeur aberrante affecte la corrélation.

Cliquez ici pour ouvrir cette simulation dans sa propre fenêtre.

Pour voir comment une valeur aberrante affecte la corrélation, faites ce qui suit :

1. Remplir le nuage de points avec une hypothétique relation linéaire positive entre X et Y (en cliquant sur le graphique une douzaine de fois en commençant en bas à gauche et en remontant en diagonale jusqu’en haut à droite). Faites attention au coefficient de corrélation calculé en haut à gauche de la simulation. (Cliquer sur la poubelle vous permet de recommencer.)
2. Une fois que vous êtes satisfait de vos données hypothétiques, créez une valeur aberrante en cliquant sur l’un des points de données en haut à droite du graphique et en le faisant glisser vers le bas le long du côté droit du graphique. Encore une fois, faites attention à ce qui arrive à la valeur de la corrélation.

Qu’est-ce que cette activité a illustré ? Cette activité illustre le fait que la corrélation diminue lorsque la valeur aberrante s’écarte du modèle de la relation. En faisant glisser un point de données de la partie supérieure droite vers la partie inférieure droite, vous avez créé une valeur aberrante qui ne correspond pas à l’association positive du reste des données. Cela diminue la force de la relation linéaire et entraîne une diminution de r .

Dans l’activité suivante, vous verrez comment la corrélation augmente lorsque la valeur aberrante est cohérente avec la direction de la relation linéaire.

Résumons

• Un cas particulier de relation entre deux variables quantitatives est la relation linéaire dans laquelle une ligne droite résume simplement et adéquatement la relation.
• Lorsque le nuage de points affiche une relation linéaire, nous le complétons par le coefficient de corrélation (r), qui mesure la force et la direction d’une relation linéaire entre deux variables quantitatives. La corrélation varie entre -1 et 1. Les valeurs proches de -1 indiquent une relation linéaire négative forte, les valeurs proches de 0 indiquent une relation linéaire faible et les valeurs proches de 1 indiquent une relation linéaire positive forte.
• La corrélation est une mesure numérique appropriée uniquement pour les relations linéaires et est sensible aux valeurs aberrantes. Par conséquent, la corrélation ne doit être utilisée qu’en complément d’un nuage de points (après avoir examiné les données).