Le centre de gravité est une propriété géométrique de tout objet.Le centre de gravité est l’emplacement moyen du poidsd’un objet. Nous pouvons décrire complètement le mouvement d’un objet dans l’espace en termes de translation du centre de gravité de l’objet d’un endroit à un autre, et de rotation de l’objet autour de son centre de gravité s’il est libre de tourner. Si l’objet est confiné pour tourner autour d’un autre point, comme une charnière, nous pouvons encore décrire son mouvement.En vol, les avions et les fusées tournent autour de leur centre de gravité.Un cerf-volant, en revanche, tourne autour du point de bride.Mais l’élancement d’un cerf-volant dépend toujours de l’emplacement du centre de gravité par rapport au point de bride, car pour tout objet, le poids agit toujours par le centre de gravité.
Déterminer le centre de gravité est très important pour tout objet volant.Comment les ingénieurs déterminent-ils l’emplacement du centre de gravité d’un avion qu’ils conçoivent ?
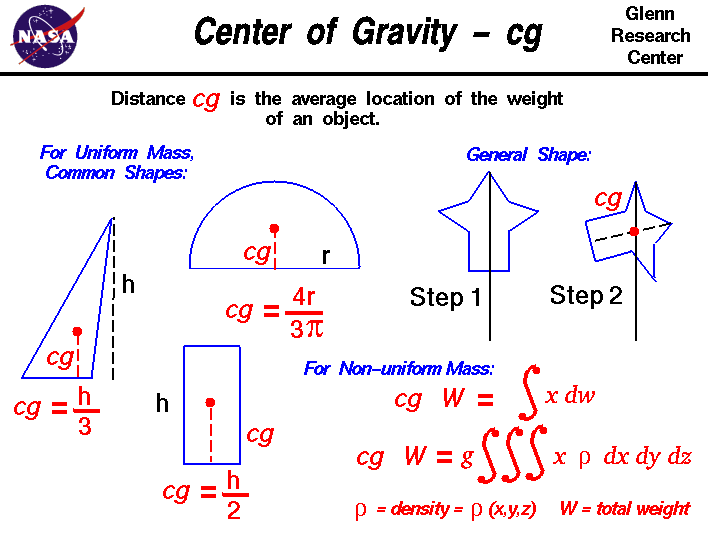
En général, la détermination du centre de gravité (cg) est une procédure compliquée car la masse (et le poids) peuvent ne pas être répartis uniformément dans l’objet. Le cas général nécessite l’utilisation de calculs que nous aborderons au bas de cette page.Si la masse est uniformément répartie, le problème est grandement simplifié.Si l’objet a une ligne (ou un plan) de symétrie, le cg se trouve sur la ligne de symétrie.Pour un bloc solide de matériau uniforme, le centre de gravité se trouve simplement à l’emplacement moyen des dimensions physiques. Pour un triangle de hauteur h, le centre de gravité se trouve à h/3, et pour un demi-cercle de rayon r, le centre de gravité se trouve à (4*r/(3*pi)) où pi est le rapport entre la circonférence du cercle et son diamètre. Les livres de mathématiques et de sciences contiennent des tableaux indiquant l’emplacement du centre de gravité de nombreuses formes simples. Les tableaux ont été générés en utilisant l’équation de calcul présentée sur la diapositive.
Pour un objet de forme générale, il existe une façon mécanique simple de déterminer le centre de gravité :
- Si nous équilibrons simplement l’objet à l’aide d’une corde ou d’une arête, le point auquel l’objet est équilibré est le centre de gravité. (Tout comme l’équilibre d’un crayon sur votre doigt !)
- Une autre façon, plus compliquée, est une méthode en deux étapes montrée sur la diapositive. Dans l’étape 1, vous suspendez l’objet à un point quelconque et vous laissez tomber une corde lestée à partir du même point. Tracez une ligne sur l’objet le long de la ficelle. Pour l’étape 2, répétez la procédure depuis un autre point de l’objet. Vous avez maintenant deux lignes tracées sur l’objet qui se croisent. Le centre de gravité est le point où les lignes se croisent. Cette procédure fonctionne bien pour les objets de forme irrégulière qui sont difficiles à équilibrer.
Si la masse de l’objet n’est pas uniformément répartie, nous devons utiliser le calculustour déterminer le centre de gravité.Nous utiliserons le symbole S dw pour désigner l’intégration d’une fonction continue par rapport au poids. On peut alors déterminer le centre de gravité à partir de :
cg * W = S x dw
où x est la distance à une ligne de référence, dw est un incrément de poids, etW est le poids total de l’objet. Pour évaluer le côté droit, nous devons déterminer comment le poids varie géométriquement. À partir de l’équation du poids, nous savons que :
w = m * g
où m est la masse de l’objet, et g est la constante gravitationnelle. À son tour, la masse m de tout objet est égale à la densité, rho, de l’objet multipliée par le volume, V :
m = rho * V
On peut combiner les deux dernières équations :
w = g * rho * V
alors
dw = g * rho * dV
dw = g * rho(x,y,z) * dx dy dz
Si nous avons une forme fonctionnelle pour la distribution de la masse, nous pouvons résoudre l’équation pour le centre de gravité :
cg * W = g * SSS x * rho(x,y,z) dx dy dz
où SSS indique une triple intégrale sur dx. dy. et dz.Si nous ne connaissons pas la forme fonctionnelle de la distribution de masse,nous pouvons intégrer numériquement l’équation en utilisant un tableur.Diviser la distance en un certain nombre de petits segments de volume etdéterminer la valeur moyenne du poids/volume (densité fois gravité) sur ce petit segment. En prenant la somme de la valeur moyenne du poids/volume fois la distance fois le segment de volumedivisé par le poids, on obtient le centre de gravité.
Vous pouvez visionner un court-métrage de « Orville et Wilbur Wright » expliquant comment le centre de gravité a affecté le vol de leur avion. Le fichier du film peut être enregistré sur votre ordinateur et visionné comme un podcast sur votre lecteur de podcasts.
Activités :![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Visites guidées
-
 Poids de l’avion :
Poids de l’avion : 
-
 Fuselage :
Fuselage : 
Navigation .
![]()
![]()
![]()
![]()
![]()
Page d’accueil du Guide du débutant