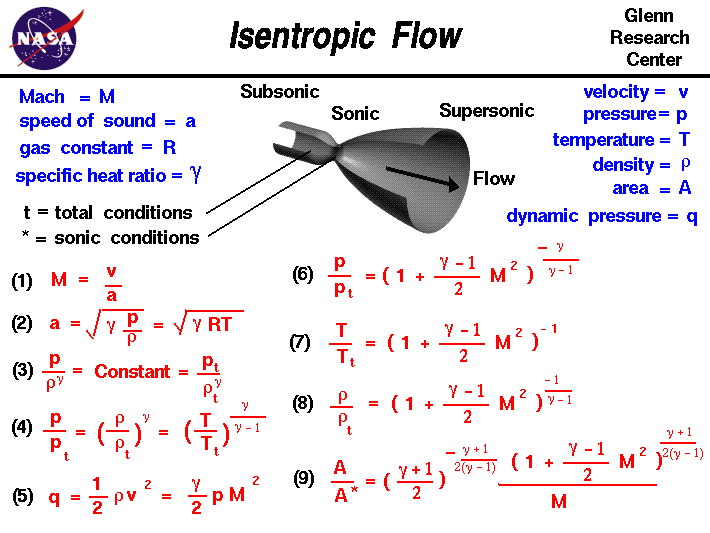
Lorsqu’un gaz est forcé à travers un tube, les molécules de gaz sont déviées par les parois du tube. Si la vitesse du gaz est bien inférieure à la vitesse du son du gaz, la densité du gaz reste constante et la vitesse de l’écoulement augmente.Cependant, lorsque la vitesse de l’écoulement s’approche de la vitesse du son, nous devons tenir compte des effets de compressibilité sur le gaz. Si l’on considère l’écoulement dans un tube, comme le montre la figure, si l’écoulement est très progressivement comprimé (la surface diminue) puis progressivement détendu (la surface augmente), les conditions d’écoulement reviennent à leur valeur initiale. Nous disons qu’un tel processus est réversible.D’après une considération de la seconde lawof thermodynamique,un écoulement réversible maintient une valeur constante d’entropie.Les ingénieurs appellent ce type d’écoulement un écoulement isentropique;une combinaison du mot grec « iso » (même) et de l’entropie.
Les écoulements isentropiques se produisent lorsque le changement des variables de l’écoulement est faible et graduel, comme l’écoulement idéal à travers les buses illustrées ci-dessus.La génération d’ondes sonores est un processus isentropique. Un écoulement supersonique qui est tourné alors que la surface de l’écoulement augmente est également isentropique.Nous appelons cela une expansion isentropique à cause de l’augmentation de la surface.Si un écoulement supersonique est tourné abruptement et que la surface de l’écoulement diminue,des ondes de choc sont générées et l’écoulement est irréversible.Les relations isentropiques ne sont plus valides et l’écoulement est gouverné par les relations de choc oblique ou normal.
Sur cette diapositive, nous avons rassemblé plusieurs des équations importantes qui décrivent un écoulement isentropique. Nous commençons par la définition du nombre de Mach puisque ceparamètreapparaît dans de nombreuses équations d’écoulement isentropique.Le nombre de Mach M est le rapport de la vitesse de l’écoulement v sur la vitesse du son a.
Eq #1 :
La vitesse du son, à son tour, dépend de ladensité r, de la pression, p, de latempérature, T,et du rapport des chaleurs spécifiques gam :
Eq #2 :
où R est la constante des gaz issue des équations d’état. Si l’on commence par les équations de l’entropie d’un gaz, on peut montrer que la pression et la densité d’un écoulement isentropique sont liées comme suit :
Eq #3 :
Nous pouvons déterminer la valeur de la constante en définissant les conditions totales comme étant la pression et la densité lorsque l’écoulement est amené au repos de façon isentropique.L’indice « t » utilisé dans beaucoup de ces équations signifie « conditions totales ». (Vous avez probablement déjà une idée des conditions totales grâce à votre expérience de l’équation de Bernoulli).
Eq #3 :
En utilisant l’équation d’état, nous pouvons facilement déduire les relations suivantes de l’équation (3) :
Eq #4 :
La pression dynamique q est définie comme étant:
Eq #5 :
En utilisant la conservation de la masse, de la quantité de mouvement et de l’énergie et la définition de l’enthalpie totale dans l’écoulement, on candère les relations suivantes :
Eq #6 :
Eq #7 :
Eq #8 :
En considérant ensuite l’équation du débit massique compressible.nous pouvons dériver:
Eq #9 :
Les conditions étoilées se produisent lorsque l’écoulement est étouffé et que le nombre de Mach est égal à un.Remarquez le rôle important que joue le nombre de Mach dans toutes les équations de la partie droite de cette diapositive. Si le nombre de Mach de l’écoulement est déterminé, toutes les autres relations d’écoulement peuvent être déterminées. De même, la détermination de n’importe quelle relation d’écoulement (rapport de pression par exemple) permettra de fixer le nombre de Mach et de définir toutes les autres conditions d’écoulement.
Voici un programme JavaScript qui résout les équations données sur cette diapositive.
Calculer
Vous sélectionnez une variable d’entrée en utilisant le bouton de choix intitulé InputVariable. A côté de la sélection, vous tapez ensuite la valeur de la variable sélectionnée. Lorsque vous appuyez sur le bouton rouge COMPUTER, les valeurs de sortie changent. Certaines variables (comme le rapport de surface) ont une double valeur. Cela signifie que pour le même rapport de surface, il existe une solution subsonique et une solution supersonique. Le bouton de choix en haut à droite sélectionne la solution qui est présentée.La variable « Wcor/A » est la fonction du débit d’air corrigé par unité de surface qui peut être dérivée du débit massique compressible.Cette variable est seulement une fonction du nombre de Mach de l’écoulement. L’angle de Mach et l’angle de Prandtl-Meyer sont également des fonctions du nombre de Mach.Ces variables supplémentaires sont utilisées dans la conception d’inlets, de buses et de conduits à grande vitesse.
Si vous êtes un utilisateur expérimenté de cette calculatrice, vous pouvez utiliser une version allégée du programme qui se charge plus rapidement sur votre ordinateur et n’inclut pas ces instructions.Vous pouvez également télécharger votre propre copie du programme pour l’exécuter hors ligne en cliquant sur ce bouton:
![]()
Activités:
Visites guidées
-
 Aérodynamique compressible :
Aérodynamique compressible : 
-
 Ondes sonores :
Ondes sonores : 
-
 Calculateur d’écoulement isentropique :
Calculateur d’écoulement isentropique : 
-
 Simulateur de buse :
Simulateur de buse : 
Navigation .
![]()
![]()
![]()
![]()
![]()
Beginner’s Guide Home Page