Les origines de la géométrie
Les premières lignes que les hommes ont imaginées étaient des lignes droites et des cercles. Elles ont marqué la naissance de la géométrie, qui signifie littéralement « Mesure de la Terre », nous donnant une idée précise de la destination de ces lignes. Les premiers experts en géométrie étaient des géomètres dans l’Égypte ancienne. Les Grecs les appellent « arpedonapti » – ceux qui nouent les cordes. Les experts égyptiens tendaient des cordes sur le terrain pour marquer les lignes et les cercles. Des traces de cet ancien usage sont encore présentes dans de nombreuses langues modernes, par exemple dans l’expression « tracer une ligne ». L’emploi de cordes pour les opérations de mesure du terrain est resté inchangé pendant plusieurs siècles et on le retrouve encore dans le travail des géomètres à une époque relativement récente.
Les historiens grecs témoignent de la naissance de la géométrie (littéralement:mesure de la terre)en Égypte. Hérodote raconte :
Si le fleuve avait simplement annulé les frontières de la parcelle de terre,c’était le rôle des officiels de redessiner les divisions exactes.
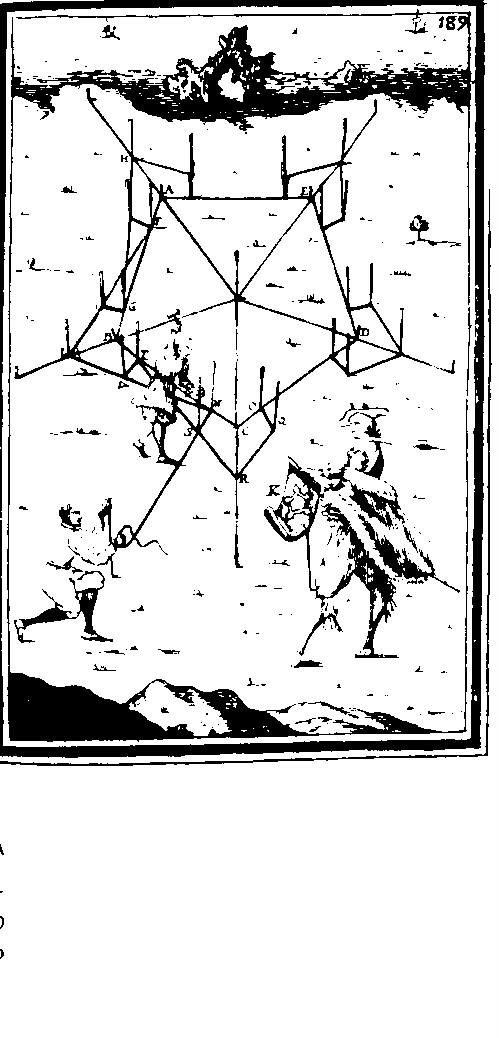 Les experts égyptiens en géométrie étaient appelés « arpedonapti », ceux qui nouent les cordes. C’est en tendant des cordes qu’ils dessinaient les deux lignes les plus simples et les plus importantes en géométrie : la ligne droite et le cercle. La première, en tendant simplement une corde entre deux points, une sorte d’opération dont l’image est encore présente dans les expressions « tracer une ligne », « tracer une perpendiculaire » ; la seconde, en faisant tourner l’un des deux points autour de l’autre qui est maintenu fixe. Pouvaient-ils imaginer l’ampleur du développement de ces deux pratiques élémentaires ? Très probablement pas. En fait, les besoins pratiques des anciens mesureurs du pays auraient rapidement fait apparaître la nécessité de travaux du type de ceux que nous appelons aujourd’hui « avec l’équerre et le compas » et qui devraient plus justement être appelés « avec les cercles et les lignes droites ».
Les experts égyptiens en géométrie étaient appelés « arpedonapti », ceux qui nouent les cordes. C’est en tendant des cordes qu’ils dessinaient les deux lignes les plus simples et les plus importantes en géométrie : la ligne droite et le cercle. La première, en tendant simplement une corde entre deux points, une sorte d’opération dont l’image est encore présente dans les expressions « tracer une ligne », « tracer une perpendiculaire » ; la seconde, en faisant tourner l’un des deux points autour de l’autre qui est maintenu fixe. Pouvaient-ils imaginer l’ampleur du développement de ces deux pratiques élémentaires ? Très probablement pas. En fait, les besoins pratiques des anciens mesureurs du pays auraient rapidement fait apparaître la nécessité de travaux du type de ceux que nous appelons aujourd’hui « avec l’équerre et le compas » et qui devraient plus justement être appelés « avec les cercles et les lignes droites ».
De nos jours, il est si naturel de considérer le papier comme l’arène naturelle de la géométrie, que nous concevons l’usage de l’équerre et du compas seuls, comme une limite arbitraire introduite par des esprits spéculatifs qui préféraient quelques nombres d’axiomes aux multiples conforts dérivant de la multiplicité des instruments. Par conséquent, la différence entre l’expert en géométrie théorique – je me réfère naturellement au classique, à l’euclidien – et le technicien – celui qui prend des mesures, l’architecte – réside principalement dans le fait que le premier décide, volontairement, de ne pas utiliser les instruments, équerres et pantographes, que le second utilise à son avantage.
De cette façon, nous avons tendance à ignorer complètement la géométrie « sur le terrain » en faveur de celle « sur le papier », ceci en omettant de reconnaître que lorsque nous transférons les opérations géométriques du terrain au papier, elles exigeront des techniques et des méthodes parfois totalement différentes.
Il ne faut pas négliger le fait que la précision d’un plan est bien plus nécessaire sur le terrain (à celui qui mesure et divise en parties un terrain, ainsi qu’à l’architecte qui construit des bâtiments – le plus souvent ces deux-là étant la même personne-) que sur le papier.L’architecte qui a une idée claire du plan d’ensemble et qui se souvient du processus qu’il a suivi pour le réaliser aurait besoin d’un brouillon. Les cartes relativement récentes, mais aussi les cartes anciennes qui ont été, inévitablement, dessinées avec des instruments et des supports rudimentaires, ne reproduisent pas exactement les limites d’un terrain. En fait, cela est impossible car même une erreur d’un point de pourcentage – le moins qui puisse se produire à une échelle raisonnablement grande – donnerait naissance à une erreur absolue qui pourrait difficilement être acceptée sur le terrain. Dans ce cas, la connaissance de la forme et des mesures de l’objet à décrire (un champ, un bâtiment), est fondamentale ; il appartiendra au géomètre de reproduire sur le terrain la précision qui fait défaut sur le papier. Il en va de même pour le mathématicien pour qui la précision des figures n’est pas du tout utile dans les démonstrations. La géométrie sur papier substitue à la précision des opérations sur le terrain, la géométrie du processus mental.
Au contraire, de la logique à l’exactitude matérielle, par suite de l’agrandissement d’échelle nécessaire pour passer du plan à sa réalisation effective, l’action de tendre une corde est restée l’une des principales opérations depuis aussi loin que l’Égypte ancienne et la Grèce antique. Cette pratique s’est maintenue jusqu’à l’époque moderne, dépassée seulement par l’invention et le perfectionnement de certains instruments d’optique. Si, sur le papier, il est assez facile de tracer une perpendiculaire à l’aide de règles et d’équerres, la même opération sur le terrain, avec le même degré de précision, exige des méthodes radicalement différentes. Sur le terrain, l’équerre est inutile car elle est trop petite par rapport aux dimensions des formes. Même si l’équerre est extrêmement précise, la perpendiculaire qu’elle peut tracer atteindra au maximum plus ou moins un mètre. Si nous devons marquer un carré de 30 mètres de côté, nous devons prolonger cette ligne 30 fois. Cette opération serait tellement inexacte qu’elle aboutirait probablement aux mêmes résultats que si nous mesurions approximativement l’angle droit.
 Ces réflexions nous ramènent à la question initiale : quelles techniques utilisaient les mesureurs égyptiens pour tracer un terrain carré ? Comment obtenaient-ils un angle carré ?
Ces réflexions nous ramènent à la question initiale : quelles techniques utilisaient les mesureurs égyptiens pour tracer un terrain carré ? Comment obtenaient-ils un angle carré ?
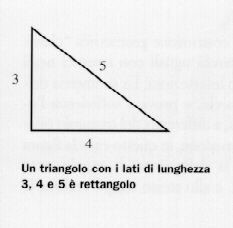
Comme l’ont suggéré certains chercheurs, il est possible qu’ils aient eu la connaissance du théorème de Pythagore ( VIe siècle avant J.-C.) ou, plus exactement, laconscience de son contraire, c’est-à-dire le fait qu’un triangle dont les côtés mesurent 3, 4 et 5, et dont le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, est un triangle rectangle. Par conséquent, si nous tendons une corde en anneau d’une longueur de 12 unités, marquée en trois points à une distance de 3, 4 et 5, vers la forme d’un triangle dont le sommet se trouve aux points marqués, l’angle entre les côtés les plus courts du triangle est un angle droit.
On ne sait pas si c’est le procédé que les anciens arpenteurs utilisaient à leur époque car il n’a pas été prouvé que les anciens Égyptiens savaient que letriangle dont les côtés sont 3, 4 et 5 est un triangle rectangle. Même s’ils étaient au courant de cela, ou d’autres triangles pythagoriciens (comme le suggère fortement la présence de plusieurs trios pythagoriciens, sinon dans les mathématiques égyptiennes, du moins dans celles de Babylone), cela implique nécessairement qu’ils connaissaient la nature de l’angle droit, ou du moins la façon de le créer.
D’où venait cette connaissance ? En raison de l’absence de documentation même partielle et de témoins, nous pouvons essayer d’aborder le problème d’un point de vue différent, mathématique plutôt qu’historique. La question que nous devons poser est la suivante : qu’est-ce qui différencie un angle droit des autres ? ou mieux, quelle est la particularité de l’angle du triangle avec les côtés 3, 4 et 5 ?
La réponse immédiate est la suivante : à la différence des autrestriangles, ceux de Pythagore et plus particulièrement le plus simple d’entre eux,celui dont les côtés sont 3, 4 et 5, on peut les faire s’emboîter en les tournant d’un côté puis de l’autre. De cette façon, on obtient une configuration symétrique qui remplit totalement tout l’espace disponible sans chevauchement ni vide.
 Aucun autre angle que le droit ne présente cette caractéristique symétrique qui trouve sa propre définition dans le premier livre complet de géométrie parvenu à notre époque, les Éléments d’Euclide (IVe siècle av. J.-C.) :
Aucun autre angle que le droit ne présente cette caractéristique symétrique qui trouve sa propre définition dans le premier livre complet de géométrie parvenu à notre époque, les Éléments d’Euclide (IVe siècle av. J.-C.) :
Quand une droite tombant sur une autre forme des angles égaux, ce sont deux droites.
La nature de l’angle droit réside dans le fait que les angles résultant de l’intersection de deux droites sont égaux. Ceci peut être immédiatementdémontré sur le papier en pliant le papier le long d’une des lignes convergentes et en vérifiant que l’autre ligne se replie sur elle-même.
La construction géométrique « classique » quiconsiste à marquer deux cercles puis à unifier leurs intersections possède également cette propriété.Le caractère symétrique de la forme est tout à fait évident, et c’est une preuve évidente de l’égalité des angles. De plus, contrairement au triangle de Pythagore qui nécessite une construction supplémentaire, dans ce cas la forme suggère immédiatement la définition de l’angle carré par l’égalité des angles et en même temps, se construit elle-même.
Ce sont encore de simples suppositions. Sans aucun doute, ce processus estdéfinitivement plus simple et d’une plus grande précision que le premier. On pourrait dire de cette manière que nous ne pouvons que marquer la perpendiculaire qui passe par le centre du segment donné, appelé aussi axe de ce segment. Néanmoins, il n’est pas difficile de remarquer que si nous avons besoin d’une perpendiculaire sur une extrémité, comme dans le cas du dessin d’un carré, il faudra doubler le segment en le prolongeant vers l’endroit où nous voulons tracer la perpendiculaire et ensuite répéter le processus précédent.Il faut observer que toutes ces techniques sont particulièrement adaptées aux terrains plats comme la plaine égyptienne.