4.2 : Moment magnétique et couple

Moment dipolaire magnétique

Nous introduisons ici un raccourci pour les futurs calculs de couple. La quantité \(yz\) est l’aire de la boucle, \(A\). Dans des applications futures, nous pourrons faire en sorte que le courant soit amené dans la boucle par un seul fil, qui est enroulé plusieurs fois autour du périmètre. La force exercée de chaque côté de la boucle (et donc le couple) sera alors multipliée par le nombre de tours du fil, \(N\). Le produit de \(N\), \(I\), et \(A\) s’écrit comme une seule quantité \(\mu\), donnant à la magnitude du couple pour ce cas la forme simple de \(\tau = \mu B\).

Si cette boucle tourne sur son axe, alors le bras de moment se rétrécit. Par exemple, si le haut de la boucle tourne vers l’arrière et le bas tourne vers l’avant de \(90^o\), alors les forces sur ces segments seront directement éloignées les unes des autres. Ces forces agissent directement à travers l’axe, le couple qu’elles produisent est donc nul. Nous savons que le couple et le champ magnétique sont tous deux des vecteurs, et le couple créé est lié à l’orientation de la boucle dans le champ. Nous pouvons rendre compte de l’orientation de la boucle en définissant un moment dipolaire magnétique :

Le vecteur \(\overrightarrow A\) a une magnitude égale à l’aire de la boucle, et a une direction qui est perpendiculaire au plan de la boucle, dans la direction définie comme suit : Courbez les doigts de votre main droite dans une direction qui trace le sens du courant autour de la boucle, et le pouce de cette main pointe la direction du vecteur. Par exemple, la boucle de la figure 4.2.1 aurait un moment magnétique qui pointe vers l’extérieur de la page.

Le vecteur couple peut maintenant être calculé à partir du moment dipolaire magnétique de la même manière que le couple exercé sur un dipôle électrique a été calculé :

Nous pouvons voir que cela fonctionne pour le cas présenté dans la figure 4.2.1 : L’angle entre le moment du dipôle magnétique (qui pointe vers l’extérieur de la page) et le champ magnétique est \(90^o\), donc le sinus de l’angle entre ces vecteurs qui apparaît dans le produit en croix est 1, ce qui donne la réponse que nous avons trouvée ci-dessus. Lorsque la boucle tourne autour de l’axe horizontal, l’angle entre le moment dipolaire magnétique et le champ change, réduisant les bras de moment des forces par un facteur de \(\sin\theta\) – exactement la quantité prise en compte dans le produit en croix. Lorsque la boucle tourne jusqu’au point où son plan est perpendiculaire au champ, le moment magnétique et le champ sont parallèles, ce qui rend le couple nul, comme nous l’avons constaté ci-dessus.

Bien que nous ayons dérivé la formule du moment dipolaire magnétique en utilisant un rectangle, il s’avère que tant que la boucle se trouve dans un plan, la formule fonctionne quelle que soit sa forme. À titre d’exemple, nous allons résoudre le couple sur une boucle circulaire. Cet exemple est plus difficile que celui du rectangle, pour des raisons qui deviendront claires, mais il démontre des outils importants pour intégrer les contributions infinitésimales et traiter les produits vectoriels.

Figure 4.2.2a – Couple sur une boucle circulaire fermée de fil dans un champ magnétique uniforme

Comme nous l’avons fait pour l’intégration des distributions de charges afin d’obtenir des champs, nous commençons par introduire un système de coordonnées (assurez-vous qu’il est à droite, c’est-à-dire.c’est-à-dire choisir les axes de sorte que \(\widehat i \times \widehat j = \widehat k\)), sélectionner un morceau infinitésimal os de la boucle, et le décrire en termes de coordonnées, en étiquetant toutes les variables que nous aurons besoin de connaître en cours de route.

Figure 4.2.2b – Couple sur une boucle circulaire fermée de fil dans un champ magnétique uniforme

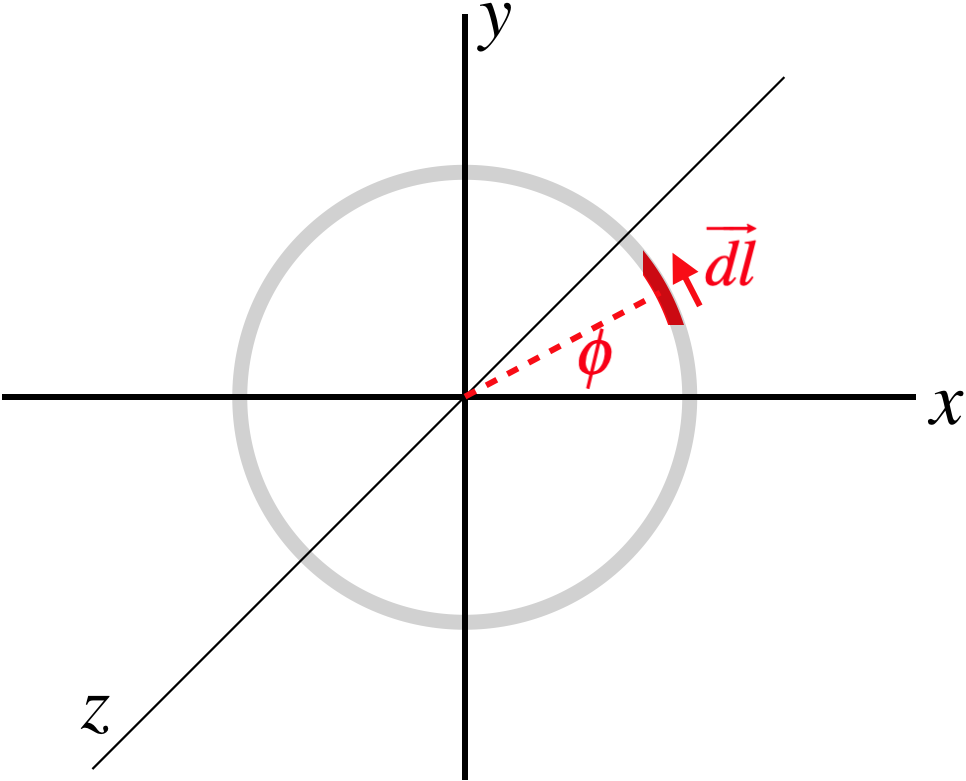
Ici, nous avons choisi de placer la boucle dans le plan \(x\)-\(y\), et le champ magnétique pointe dans la direction \(+x\). Une tranche infinitésimale de fil a été sélectionnée à un angle \(\phi\) vers le haut de l’axe \(+x\)-.

Puis nous devons exprimer mathématiquement le vecteur \(\overrightarrow {dl}\). Sa magnitude est la longueur d’un segment d’arc infinitésimal, soit \(R\;d\phi\). La direction est plus délicate à trouver, mais en gonflant l’image et en faisant un peu de géométrie, on peut déterminer ses composantes :

Figure 4.2.3 – Écriture du vecteur de l’élément courant

Mise en commun en un seul vecteur :

\

Nous avons maintenant tout ce dont nous avons besoin. Aussi compliquée que soit la géométrie avec la force puis le couple, nous n’avons pas besoin de la suivre – tout ce dont nous avons besoin est de faire le calcul vectoriel correctement. Par exemple, la force sur l’élément actuel est :

Gauche]

Rappelant les produits croisés des vecteurs unitaires de la physique 9A, nous branchons \(\widehat i\times\widehat i = 0\) et \(\widehat j\times\widehat i = -\widehat k\), et la force sur cet élément devient :

Pour obtenir le couple, on choisit l’origine comme point de référence, et on calcule directement la contribution infinitésimale au couple. En branchant le vecteur de position et en faisant les mathématiques vectorielles, on obtient :

Il ne reste plus qu’à additionner toutes les contributions au couple, ce qui revient à intégrer sur l’angle \(\phi\) de \(0\rightarrow 2\pi\) 🙂

\N = IR^2B\left=I\left(\pi R^2\right)B\;\widehat j\]

Sure enough, the magnitude of the torque comes out to be \(\mu\;B\), where \(\mu=IA\). Et l’utilisation de la règle de la main droite pour obtenir la direction du moment magnétique (hors de la page) suivie de la direction du couple de la règle de la main droite appliquée à \(\overrightarrow\mu\times\overrightarrow B\), confirme que la direction fonctionne également.

Ce problème semblait très intimidant car la direction de \(\overrightarrow {dl}\) change partout sur le cercle, mais une fois que ce vecteur est écrit en termes de \(\phi\) et des vecteurs unitaires, les mathématiques font le reste !