Suivant : 17.3 Nombres adimensionnels et Up : 17. Transfert de chaleur par convection Previous : 17.1 L’analogie de Reynolds Contents Index
Nous pouvons maintenant analyser des problèmes dans lesquels la conduction et la convection ont lieu, en commençant par une paroi refroidie par un fluide en écoulement de chaque côté. Comme nous l’avons discuté, une description du transfert de chaleur par convection peut être donnée explicitement sous la forme
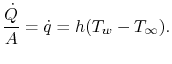
Ceci pourrait représenter un modèle d’aube de turbine avec refroidissement interne. La figure 17.6 illustre cette configuration.
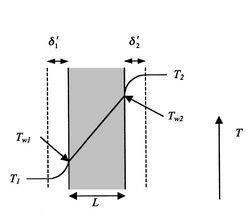
.
Le transfert de chaleur dans le fluide 1 est donné par
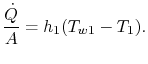
qui est le transfert de chaleur par unité de surface vers le fluide. Le transfert de chaleur dans le fluide 2 est de même donné par
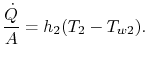
De l’autre côté du mur, on a
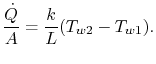
La quantité![]() est la même dans toutes ces expressions.En les mettant bout à bout pour écrire la chute de température globale connue, on obtient une relation entre transfert de chaleur et chute de température globale,
est la même dans toutes ces expressions.En les mettant bout à bout pour écrire la chute de température globale connue, on obtient une relation entre transfert de chaleur et chute de température globale,![]() :
:
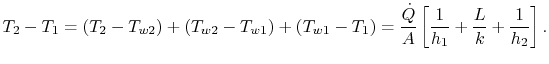 |
(17..20) |
Nous pouvons définir une résistance thermique,![]() , comme précédemment, telle que
, comme précédemment, telle que
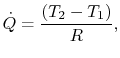
où![]() est donné par
est donné par
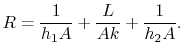 |
(17..21) |
L’équation (17.21) est la résistance thermique pour une paroi solide avec un transfert de chaleur par convection de chaque côté.
Pour une aube de turbine dans un moteur à turbine à gaz, le refroidissement est une considération critique. En termes de figure 17.6, ![]() est la température en sortie de chambre de combustion (entrée de turbine) et
est la température en sortie de chambre de combustion (entrée de turbine) et ![]() est la température en sortie de compresseur. On souhaite trouver
est la température en sortie de compresseur. On souhaite trouver ![]() car c’est la température la plus élevée du métal. D’après(17.20), la température de paroi peut être écrite comme
car c’est la température la plus élevée du métal. D’après(17.20), la température de paroi peut être écrite comme
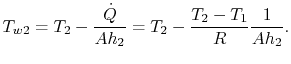 |
(17..22) |
En utilisant l’expression de la résistance thermique, les températures des parois peuvent être exprimées en termes de coefficients de transfert de chaleur et de propriétés des parois comme suit :
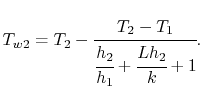 |
(17..23) |
L’équation (17.23) fournit quelques lignes directrices de base pour la conception. L’objectif est d’avoir une faible valeur de![]() . Cela signifie que
. Cela signifie que![]() doit être grand,
doit être grand,![]() doit être grand (mais nous n’aurons peut-être pas beaucoup de flexibilité dans le choix du matériau) et
doit être grand (mais nous n’aurons peut-être pas beaucoup de flexibilité dans le choix du matériau) et![]() doit être petit. Une façon d’atteindre la première de ces conditions est d’avoir
doit être petit. Une façon d’atteindre la première de ces conditions est d’avoir![]() faible (par exemple, pour faire sortir l’air de refroidissement comme dans laFigure 17.1 pour protéger la surface).
faible (par exemple, pour faire sortir l’air de refroidissement comme dans laFigure 17.1 pour protéger la surface).
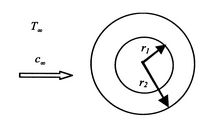
Un deuxième exemple de conduction et de convection combinées est donné par un cylindre exposé à un fluide en mouvement. La géométrie est présentée dans laFigure 17.7.
Pour le cylindre, le flux thermique à la surface extérieure est donné par
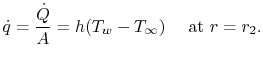
La condition limite à la surface interne pourrait être soit une condition de flux de chaleur, soit une spécification de température ; nous utilisons cette dernière pour simplifier l’algèbre. Ainsi,![]()
![]() . Il s’agit d’un modèle de transfert thermique dans un tuyau de rayon
. Il s’agit d’un modèle de transfert thermique dans un tuyau de rayon![]() entouré d’un isolant d’épaisseur
entouré d’un isolant d’épaisseur![]() . La solution pour une région cylindrique a été donnée dans laSection 16.5.1 comme
. La solution pour une région cylindrique a été donnée dans laSection 16.5.1 comme
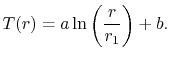
L’utilisation de la condition aux limites![]() donne
donne![]() .
.
À l’interface entre le cylindre et le fluide, ![]() , la température et le flux thermique sont continus. (Question : Pourquoi est-ce le cas ? Comment argumenteriez-vous ce point ?)
, la température et le flux thermique sont continus. (Question : Pourquoi est-ce le cas ? Comment argumenteriez-vous ce point ?)
![$\displaystyle \dot{q} = \underbrace{-k\frac{dT}{dr}}_{{substack{\textrm{heat fl......2}{r_1}\right)+T_1\right)-T_\infty\right]} _\textrm{flux de chaleur de surface vers le fluide}$](https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/img2033.png) |
(17..24) |
Placer la forme de la distribution de température dans le cylindredans l’équation (17.24) yields
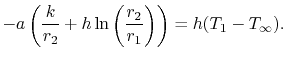
La constante d’intégration,![]() , est
, est
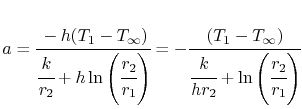
et l’expression de la température est, sous forme non dimensionnelle normalisée,
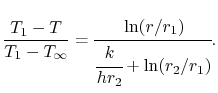 |
(17..25) |
Le flux thermique par unité de longueur,![]() , est donné par
, est donné par
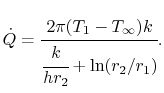 |
(17..26) |
Les unités dans l’équation (17.26) sont W/m-s.
Un problème d’intérêt est de choisir l’épaisseur de l’isolant pour minimiser les pertes de chaleur pour une différence de température fixe ![]() entre l’intérieur de la conduite et le fluide en écoulement éloigné de la conduite. (
entre l’intérieur de la conduite et le fluide en écoulement éloigné de la conduite. (![]() est la distribution de température motrice pour le tuyau). Pour comprendre le comportement du transfert de chaleur, nous examinons le dénominateur de l’équation (17.26) lorsque
est la distribution de température motrice pour le tuyau). Pour comprendre le comportement du transfert de chaleur, nous examinons le dénominateur de l’équation (17.26) lorsque ![]() varie. L’épaisseur de l’isolation qui donne un transfert de chaleur maximal est donnée par
varie. L’épaisseur de l’isolation qui donne un transfert de chaleur maximal est donnée par
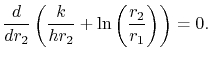 |
(17..27) |
(Question : comment savoir s’il s’agit d’un maximum ?)
D’après l’équation (17.27), la valeur de ![]() pour le maximum
pour le maximum ![]() est donc
est donc
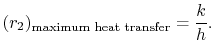 |
(17..28) |
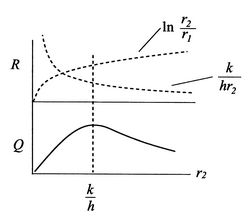
Si![]() est inférieur à cette valeur, nous pouvons ajouter de l’isolation et augmenter les pertes de chaleur. Pour comprendre pourquoi cela se produit, considérez laFigure 17.8, qui montre un schéma de la résistance thermique et du transfert de chaleur. Lorsque
est inférieur à cette valeur, nous pouvons ajouter de l’isolation et augmenter les pertes de chaleur. Pour comprendre pourquoi cela se produit, considérez laFigure 17.8, qui montre un schéma de la résistance thermique et du transfert de chaleur. Lorsque![]() augmente à partir d’une valeur inférieure à
augmente à partir d’une valeur inférieure à![]() , deux effets se produisent. Premièrement, l’épaisseur de l’isolant augmente, ce qui tend à diminuer le transfert de chaleur car le gradient de température diminue.Deuxièmement, la surface extérieure de l’isolant augmente, ce qui tend à augmenter le transfert de chaleur. Le second de ces effets est (vaguement) associé au terme
, deux effets se produisent. Premièrement, l’épaisseur de l’isolant augmente, ce qui tend à diminuer le transfert de chaleur car le gradient de température diminue.Deuxièmement, la surface extérieure de l’isolant augmente, ce qui tend à augmenter le transfert de chaleur. Le second de ces effets est (vaguement) associé au terme![]() , le premier au terme
, le premier au terme![]() . Il y a donc deux effets concurrents qui se combinent pour donner un maximum
. Il y a donc deux effets concurrents qui se combinent pour donner un maximum![]()
![]() .
.
Points névralgiques
Dans l’expression ![]() , que représente
, que représente ![]() ? (MP 17.4)
? (MP 17.4)
Il semble que nous ayons beaucoup simplifié la convection. Trouver le coefficient de transfert de chaleur, ![]() , est-il vraiment difficile ?(MP 17.5)
, est-il vraiment difficile ?(MP 17.5)
Que signifie le « K » dans la formule de la résistance de contact ?(MP 17.6)
Dans l’équation de la température dans un cylindre(17.25), que représente « r » ?(MP 17.7)
Suivant : 17.3 Nombres adimensionnels et Up : 17. Transfert de chaleur par convection Previous : 17.1 L’analogie de Reynolds Sommaire Index
UnifiedTP