Los orígenes de la geometría
Las primeras líneas que el hombre imaginó fueron líneas rectas y círculos. Éstas marcaron el nacimiento de la geometría, que significa literalmente «medida de la tierra», lo que nos da una idea precisa de para qué servían estas líneas. Los primeros expertos en geometría fueron los topógrafos del Antiguo Egipto. Los griegos los llamaban «arpedonapti», es decir, los que anudan las cuerdas. Los expertos egipcios solían tensar cuerdas en la tierra para marcar líneas y círculos. Las huellas de este antiguo uso siguen presentes en muchas lenguas modernas como, por ejemplo, en el dicho «trazar una línea». El uso de cuerdas para las operaciones de medición de la tierra ha permanecido inalterado durante varios siglos y todavía se puede encontrar en el trabajo de los topógrafos en tiempos relativamente recientes.
Los historiadores griegos dan testimonio del nacimiento de la geometría (literalmente: medición de la tierra) en Egipto. Herodoto dice:
Si el río simplemente había anulado los límites de la parcela, era función de los funcionarios volver a trazar las divisiones exactas.
 Los expertos en geometría egipcios se llamaban «arpedonapti», los que anudan cuerdas. Es apretando cuerdas como dibujaban las dos líneas más simples e importantes de la geometría: la línea recta y el círculo. La primera, simplemente tensando una cuerda entre dos puntos, un tipo de operación cuya imagen sigue presente en las expresiones «trazar una línea», «trazar una perpendicular»; la segunda, haciendo girar uno de los dos puntos alrededor del otro que se mantiene fijo. ¿Podrían imaginar el alcance del desarrollo de estas dos prácticas elementales? Probablemente no. De hecho, las necesidades prácticas de los antiguos medidores de tierras supuestamente hicieron surgir pronto la necesidad de trabajos del tipo que hoy llamamos «con escuadra y compás» y que debería llamarse más propiamente «con círculos y rectas».
Los expertos en geometría egipcios se llamaban «arpedonapti», los que anudan cuerdas. Es apretando cuerdas como dibujaban las dos líneas más simples e importantes de la geometría: la línea recta y el círculo. La primera, simplemente tensando una cuerda entre dos puntos, un tipo de operación cuya imagen sigue presente en las expresiones «trazar una línea», «trazar una perpendicular»; la segunda, haciendo girar uno de los dos puntos alrededor del otro que se mantiene fijo. ¿Podrían imaginar el alcance del desarrollo de estas dos prácticas elementales? Probablemente no. De hecho, las necesidades prácticas de los antiguos medidores de tierras supuestamente hicieron surgir pronto la necesidad de trabajos del tipo que hoy llamamos «con escuadra y compás» y que debería llamarse más propiamente «con círculos y rectas».
Hoy en día, es tan natural considerar el papel como el ámbito natural de la geometría, que concebimos el uso de escuadras y compases únicamente, como un límite arbitrario introducido por los espíritus especulativos que preferían un número reducido de axiomas a las múltiples comodidades derivadas de la multiplicidad de instrumentos. En consecuencia, la diferencia entre el geómetra teórico -me refiero naturalmente al clásico, al euclidiano- y el técnico -el que toma medidas, el arquitecto- reside principalmente en el hecho de que el primero decide, voluntariamente, no utilizar instrumentos, escuadras y pantógrafos, que el segundo utiliza en su beneficio.
Así, tendemos a ignorar por completo la geometría «en el campo» en favor de la «en el papel», no reconociendo que cuando trasladamos las operaciones geométricas del campo al papel, éstas exigen a veces técnicas y métodos totalmente diferentes.
No hay que pasar por alto el hecho de que la precisión de un plano es mucho más necesaria en el campo (para el que mide y divide en partes un terreno, así como para el arquitecto que hace edificios -la mayoría de las veces estos dos son la misma persona-) que sobre el papel.El arquitecto que tiene una idea clara del plano general y que recuerda el proceso que siguió para realizarlo necesitaría un borrador. Tanto los mapas relativamente recientes como los antiguos que, inevitablemente, fueron dibujados con instrumentos y soportes rudimentarios, no reproducen con exactitud los límites de un terreno. De hecho, esto es imposible porque incluso un error de un punto porcentual -lo mínimo que podría ocurrir en una escala razonablemente grande- daría lugar a un error absoluto que difícilmente podría aceptarse sobre el terreno. En este caso, el conocimiento de la forma y de las medidas del objeto que se va a describir (un campo, un edificio), es fundamental; será el geómetra quien deba reproducir sobre el terreno la precisión que falta en el papel. Lo mismo ocurre con el matemático, para quien la precisión de las figuras no es en absoluto útil en las demostraciones. La geometría sobre el papel sustituye la precisión de las operaciones sobre el terreno, con la geometría del proceso mental.
Por el contrario, de la lógica a la exactitud material, como consecuencia de la necesaria ampliación de la escala para pasar del plano a la creación real del mismo, la acción de tensar una cuerda ha seguido siendo una de las principales operaciones desde tan lejos como el Antiguo Egipto y la Antigua Grecia. Esta práctica se ha mantenido hasta los tiempos modernos, superada únicamente por la invención y el perfeccionamiento de ciertos instrumentos ópticos. Mientras que, sobre el papel, es bastante fácil trazar una perpendicular por medio de reglas y escuadras, la misma operación sobre el terreno, con el mismo grado de precisión, exige métodos radicalmente diferentes. En el campo, la escuadra es inútil porque es demasiado pequeña en relación con las dimensiones de las formas. Aunque la escuadra sea extremadamente precisa, la perpendicular que puede trazar alcanzará como máximo un metro. Si tenemos que marcar un cuadrado de 30 metros de lado, tendremos que prolongar esta línea 30 veces. Esto sería una operación tan inexacta que probablemente daría los mismos resultados que si midiéramos el ángulo recto de forma aproximada.
 Estas reflexiones nos devuelven a la pregunta inicial: ¿qué técnicas utilizaban los medidores egipcios para trazar un terreno cuadrado? Cómo obtenían el ángulo cuadrado?
Estas reflexiones nos devuelven a la pregunta inicial: ¿qué técnicas utilizaban los medidores egipcios para trazar un terreno cuadrado? Cómo obtenían el ángulo cuadrado?
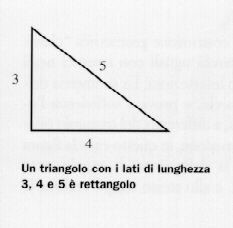
Como han sugerido algunos estudiosos, es posible que tuvieran el conocimiento del teorema de Pitágoras (siglo VI a.C.) o, más exactamente, la conciencia de su contrario, es decir, el hecho de que un triángulo con lados que miden 3, 4 y 5, en el que el cuadrado del lado más largo es igual a la suma de los cuadrados de los otros dos lados, es un triángulo rectángulo. Por lo tanto, si estiramos una cuerda anular con una longitud de 12 unidades, marcada en tres puntos a una distancia de 3, 4 y 5, hacia la forma de un triángulo con el vértice en los puntos marcados, el ángulo entre los lados más cortos del triángulo es un ángulo recto.
No se sabe si este era el proceso que utilizaban los antiguos topógrafos en su época, ya que no se ha demostrado que los antiguos egipcios supieran que el triángulo con los lados 3, 4 y 5 es un triángulo rectángulo. Incluso si eran conscientes de esto, o de otros triángulos pitagóricos (como se sugiere fuertemente por la presencia de varios tríos pitagóricos, si no en las matemáticas egipcias, entonces en las babilónicas), esto implica necesariamente que conocían la naturaleza de, o al menos cómo crear el ángulo recto.
¿De dónde vino este conocimiento? Debido a la falta de documentación y de testigos, incluso parciales, podemos intentar abordar el problema desde un punto de vista diferente, más matemático que histórico. La pregunta que debemos plantear es ¿qué hace que un ángulo recto sea diferente de los demás? O mejor, ¿cuál es la peculiaridad del ángulo del triángulo con lados 3, 4 y 5?
La respuesta inmediata es: a diferencia de otros triángulos, los pitagóricos y en particular el más sencillo de ellos, el de lados 3, 4 y 5, se pueden hacer encajar girándolos por un lado y luego por el otro. De esta manera, se obtiene una configuración simétrica que llena totalmente todo el espacio disponible sin solapamientos ni huecos.
 Ningún otro ángulo, salvo el recto, tiene esta característica de simetría que adquiere su propia definición en el primer libro completo de geometría que llegó a nuestros días, los Elementos de Euclides (siglo IV a.C.):
Ningún otro ángulo, salvo el recto, tiene esta característica de simetría que adquiere su propia definición en el primer libro completo de geometría que llegó a nuestros días, los Elementos de Euclides (siglo IV a.C.):
Cuando una recta que cae sobre otra forma ángulos iguales, estos son ambos rectos.
La naturaleza del ángulo cuadrado reside en que los ángulos resultantes de la intersección de dos rectas son iguales. Esto se puede demostrar inmediatamente sobre el papel doblando el papel a lo largo de una de las líneas convergentes y verificando que la otra línea se dobla sobre sí misma.
La construcción geométrica «clásica» que consiste en marcar dos círculos y luego unificar sus intersecciones también posee esta propiedad.El carácter simétrico de la forma es bastante evidente, y es una prueba clara de la igualdad de los ángulos. Además, a diferencia del triángulo de Pitágoras que necesita una construcción posterior, en este caso la forma sugiere inmediatamente la definición de ángulo cuadrado a través de la igualdad de los ángulos y, al mismo tiempo, se construye a sí misma.
Estas son todavía simples suposiciones. Sin duda, este proceso es definitivamente más sencillo y de mayor precisión que el anterior. Se podría decir que de esta manera sólo podemos marcar la perpendicular que pasa por el centro del segmento dado, también llamado eje de este segmento. No obstante, no es difícil darse cuenta de que si necesitamos una perpendicular en un extremo, como en el caso de dibujar un cuadrado, será necesario duplicar el segmento prolongándolo hacia donde queremos dibujar la perpendicular y luego repetir el proceso anterior.Hay que observar que todas estas técnicas son especialmente adecuadas para terrenos planos como la llanura egipcia.