El orden de las operaciones: PEMDAS

MathHelp.com

Para eliminar esta confusión, tenemos unas reglas de precedencia, establecidas al menos desde el año 1500, llamadas «orden de operaciones». Las «operaciones» son la adición, la sustracción, la multiplicación, la división, la exponenciación y la agrupación; el «orden» de estas operaciones establece qué operaciones tienen prioridad (se ocupan) antes de qué otras operaciones.

Una técnica común para recordar el orden de las operaciones es la abreviatura (o, más bien, el «acrónimo») «PEMDAS», que se convierte en la frase mnemotécnica «Please Excuse My Dear Aunt Sally». Esta frase significa, y ayuda a recordar el orden de «Paréntesis, Exponentes, Multiplicación y División, y Adición y Sustracción». Este listado indica el rango de las operaciones: Los paréntesis superan a los exponentes, que superan a la multiplicación y la división (pero la multiplicación y la división están en el mismo rango), y la multiplicación y la división superan a la suma y la resta (que están juntas en el rango inferior). En otras palabras, la precedencia es:

Cuando tienes un montón de operaciones del mismo rango, simplemente operas de izquierda a derecha. Por ejemplo, 15 ÷ 3 × 4 no es 15 ÷ (3 × 4) = 15 ÷ 12, sino que es (15 ÷ 3) × 4 = 5 × 4, porque, yendo de izquierda a derecha, se llega primero al signo de división.

Si no estás seguro de esto, pruébalo en tu calculadora, que ha sido programada con la jerarquía de orden de operaciones. Por ejemplo, escribiendo la expresión anterior en una calculadora gráfica, obtendrás:

Usando la jerarquía anterior, vemos que, en la pregunta «4 + 2×3» del principio de este artículo, la opción 2 era la respuesta correcta, porque hay que hacer la multiplicación antes de hacer la suma.

El contenido continúa a continuación

(Nota: Los hablantes del inglés británico suelen utilizar el acrónimo «BODMAS», en lugar de «PEMDAS». BODMAS significa «Brackets, Orders, Division and Multiplication, and Addition and Subtraction». Dado que «paréntesis» es lo mismo que paréntesis y «órdenes» es lo mismo que exponentes, las dos siglas significan lo mismo. Además, puede ver que la «M» y la «D» están invertidas en la versión inglesa-británica; esto confirma que la multiplicación y la división están en el mismo «rango» o «nivel». Los angloparlantes canadienses dividen la diferencia, utilizando BEDMAS.)

El orden de las operaciones se estableció para evitar la incomunicación, pero PEMDAS puede generar su propia confusión; algunos estudiantes a veces tienden a aplicar la jerarquía como si todas las operaciones de un problema estuvieran en el mismo «nivel» (simplemente yendo de izquierda a derecha), pero a menudo esas operaciones no son «iguales». Muchas veces ayuda trabajar los problemas de dentro a fuera, en lugar de ir de izquierda a derecha, porque a menudo algunas partes del problema están «más abajo» que otras. La mejor manera de explicar esto es hacer algunos ejemplos:

• Simplifica 4 + 32.

Necesito simplificar el término con el exponente antes de intentar sumar en el 4:

4 + 32 = 4 + 9 = 13

• Simplifica 4 + (2 + 1)2.

Tengo que simplificar dentro del paréntesis antes de poder sacar el exponente. Sólo entonces puedo hacer la suma del 4.

4 + (2 + 1)2 = 4 + (3)2 = 4 + 9 = 13

Anuncio

• Simplifica 4 + 2.

Afiliado

No debería intentar hacer estos paréntesis anidados de izquierda a derecha; ese método es simplemente demasiado propenso a errores. En su lugar, intentaré trabajar de dentro a fuera. Primero simplificaré dentro de los paréntesis curvos, luego simplificaré dentro de los corchetes, y sólo entonces me ocuparé del cuadrado. Una vez hecho esto, podré añadir finalmente el 4:

4 + 2

= 4 + 2

= 4 + 2

= 4 + 9

= 13

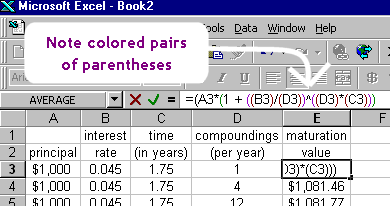
No hay ningún significado especial en el uso de los corchetes (la «» de arriba) en lugar de los paréntesis. Los corchetes y las llaves (los caracteres «{» y «}») se utilizan cuando hay paréntesis anidados, como ayuda para saber qué paréntesis van con qué. Los diferentes caracteres de agrupación se utilizan sólo por conveniencia. Esto es similar a lo que ocurre en una hoja de cálculo de Excel cuando se introduce una fórmula utilizando paréntesis: cada conjunto de paréntesis está codificado por colores, para que pueda distinguir los pares:

• Simplificar

Simplificaré primero dentro de los paréntesis:

Así que mi respuesta simplificada es

La siguiente página tiene más ejemplos trabajados….

URL: https://www.purplemath.com/modules/orderops.htm

Página 1Página 2Página 3