Un análisis de correlación o de regresión lineal simple puede determinar si dos variables numéricas están relacionadas linealmente de forma significativa. Un análisis de correlación proporciona información sobre la fuerza y la dirección de la relación lineal entre dos variables, mientras que un análisis de regresión lineal simple estima los parámetros de una ecuación lineal que puede utilizarse para predecir los valores de una variable en función de la otra.
Correlación
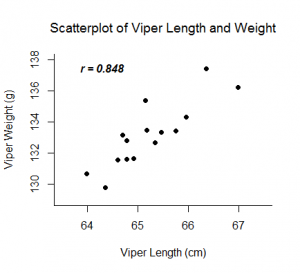
El coeficiente de correlación de Pearson, r, puede tomar valores entre -1 y 1. Cuanto más se aleje r de cero, más fuerte será la relación lineal entre las dos variables. El signo de r corresponde a la dirección de la relación. Si r es positivo, cuando una variable aumenta, la otra tiende a aumentar. Si r es negativo, cuando una variable aumenta, la otra tiende a disminuir. Una relación lineal perfecta (r=-1 o r=1) significa que una de las variables puede ser perfectamente explicada por una función lineal de la otra.
Ejemplos:

Regresión lineal
Un análisis de regresión lineal produce estimaciones para la pendiente y el intercepto de la ecuación lineal que predice una variable de resultado, Y, basándose en los valores de una variable de predicción, X. Una forma general de esta ecuación se muestra a continuación:
![]()
La intercepción, b0, es el valor predicho de Y cuando X=0. La pendiente, b1, es el cambio promedio en Y por cada aumento de una unidad en X. Además de darle la fuerza y la dirección de la relación lineal entre X e Y, la estimación de la pendiente permite una interpretación de cómo cambia Y cuando X aumenta. Esta ecuación también puede utilizarse para predecir valores de Y para un valor de X.
Ejemplos:


Se pueden realizar pruebas inferenciales tanto en la correlación como en las estimaciones de la pendiente calculadas a partir de una muestra aleatoria de una población. Ambos análisis son pruebas t ejecutadas sobre la hipótesis nula de que las dos variables no están relacionadas linealmente. Si se ejecuta con los mismos datos, una prueba de correlación y una prueba de pendiente proporcionan la misma estadística de prueba y el mismo valor p.
Supuestos:
- Muestras aleatorias
- Observaciones independientes
- La variable predictora y la variable de resultado están relacionadas linealmente (evaluadas mediante la comprobación visual de un gráfico de dispersión).
- La población de valores del resultado se distribuye normalmente para cada valor del predictor (evaluado mediante la confirmación de la normalidad de los residuos).
- La varianza de la distribución del resultado es la misma para todos los valores del predictor (evaluado mediante la comprobación visual de un gráfico de residuos para un patrón de embudo).
Hipótesis:
Ho: Las dos variables no están relacionadas linealmente.
Ha: Las dos variables están relacionadas linealmente.
Ecuaciones relevantes:
Grados de libertad: df = n-2


![]()
Ejemplo 1: Cálculo de manos
Estos vídeos investigan la relación lineal entre las alturas de las personas y las medidas de la extensión de los brazos.
Correlación:


Regresión:


Conclusión de la muestra: Al investigar la relación entre la envergadura de los brazos y la altura, encontramos una gran correlación positiva (r=.95), lo que indica una fuerte relación lineal positiva entre las dos variables. Calculamos la ecuación de la línea de mejor ajuste como Armspan=-1,27+1,01(Altura). Esto indica que para una persona que mide cero pulgadas, su envergadura predicha sería de -1,27 pulgadas. Este no es un valor posible ya que el rango de nuestros datos será mucho mayor. Por cada aumento de 1 pulgada en la altura, se predice que la envergadura de los brazos aumentará en 1,01 pulgadas.
Ejemplo 2: Realización del análisis en Excel 2016
Algunos de estos análisis requieren que tenga activado el complemento Data Analysis ToolPak en Excel. Para obtener instrucciones para realizar este análisis en versiones anteriores de Excel, visite https://stat.utexas.edu/videos
Conjunto de datos utilizado en los vídeos
Matriz de correlación y valor p:
Direcciones del PDF correspondientes al vídeo
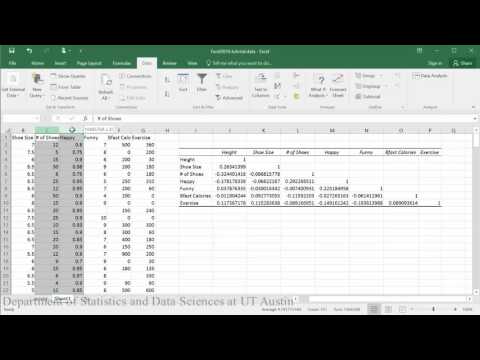

Creación de gráficos de dispersión:
Direcciones del PDF correspondientes al vídeo
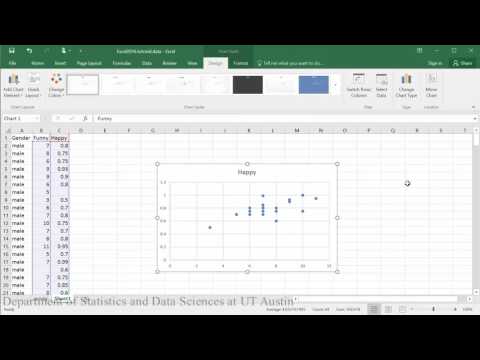

Modelo lineal (primera mitad del tutorial):
Direcciones del PDF correspondientes al vídeo
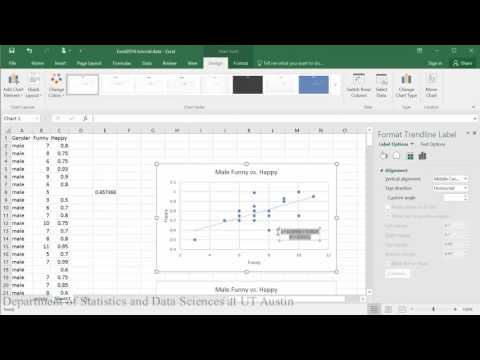

Creación de gráficos residuales:
Direcciones del PDF correspondientes al vídeo
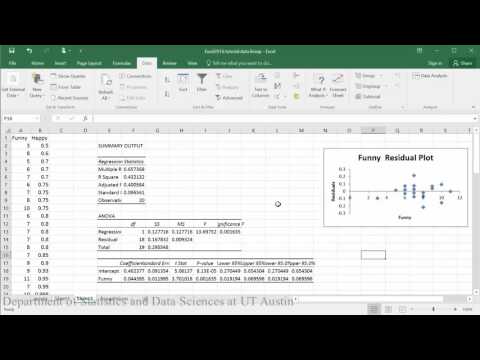

Conclusión de la muestra: Al evaluar la relación entre lo feliz que es alguien y lo divertido que lo califican los demás, el diagrama de dispersión indica que parece haber una relación lineal positiva moderadamente fuerte entre las dos variables, lo que se apoya en el coeficiente de correlación (r = .65). La comprobación de los supuestos mediante el gráfico de residuos no indicó ningún problema con los datos. La ecuación lineal para predecir la felicidad a partir de la diversión fue Happy=.04+0.46(Funny). La intersección Y indica que para una persona cuya valoración de la diversión es cero, se predice que su felicidad es de 0,04. La calificación de funny predice significativamente la felicidad de tal manera que por cada aumento de 1 punto en la calificación de funny se predice que los varones aumentan en 0,46 de felicidad (t = 3,70, p = 0,002).
Ejemplo 3: Realización de análisis en R
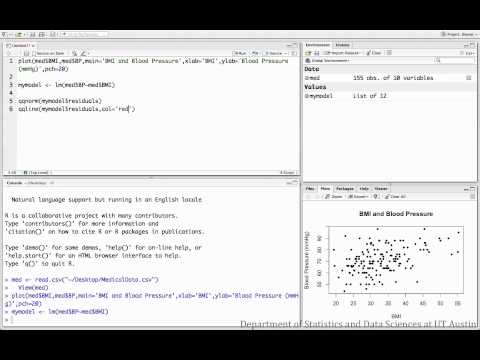
Los siguientes vídeos investigan la relación entre el IMC y la presión arterial para una muestra de pacientes médicos.
Conjunto de datos utilizado en los vídeos
Correlación:
Archivo de script de R utilizado en el vídeo
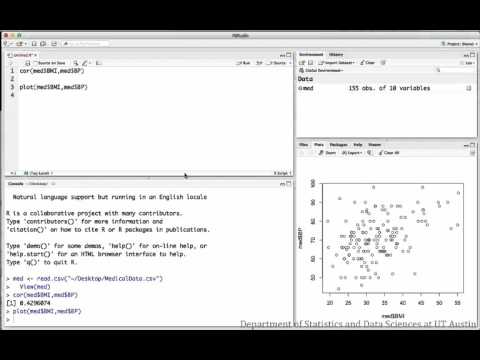

Regresión:
Archivo de script R utilizado en el vídeo