Conceptos de estadística

Propiedades de r

Ahora discutimos e ilustramos varias propiedades importantes del coeficiente de correlación como medida numérica de la fuerza de una relación lineal.

1. La correlación no cambia cuando las unidades de medida de cualquiera de las variables cambian. En otras palabras, si cambiamos las unidades de medida de la variable explicativa y/o de la variable de respuesta, no tiene ningún efecto sobre la correlación (r).

Para ilustrarlo, compare las dos versiones del diagrama de dispersión de la relación entre la edad de un conductor y la distancia máxima para leer una señal de tráfico.

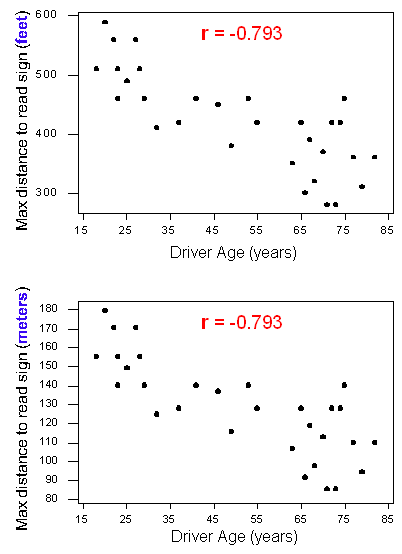
El gráfico de dispersión superior muestra los datos originales donde las distancias máximas se miden en pies. El gráfico de dispersión inferior muestra la misma relación, pero con las distancias máximas cambiadas a metros. Observe que los valores Y han cambiado, pero las correlaciones son las mismas. Este ejemplo ilustra que un cambio en las unidades no cambia r. Esto es cierto incluso si cambiamos las unidades en ambas variables. Tiene sentido porque un cambio en las unidades no cambia el patrón de los datos. La dirección, la forma y la fuerza de la relación siguen siendo las mismas. Como r mide la dirección y la fuerza de una relación lineal, el valor de r sigue siendo el mismo.

2. La correlación mide sólo la fuerza de una relación lineal entre dos variables. Ignora cualquier otro tipo de relación, por muy fuerte que sea. Por ejemplo, considere la relación entre el consumo medio de combustible al conducir una distancia fija en un coche y la velocidad a la que conduce el coche:

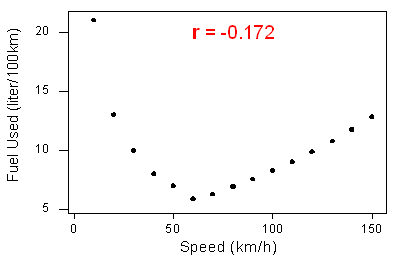
Los datos tienen una forma curvilínea suave. La relación es muy fuerte porque los datos siguen la curva perfectamente.

Nota que la correlación r = -0,172 indica una relación lineal débil. Esto tiene sentido porque los datos no siguen estrechamente una forma lineal. Así que el coeficiente de correlación sólo da información sobre la fuerza de una relación lineal. No da información fiable sobre la fuerza de una relación curvilínea.

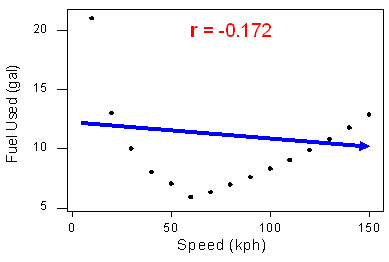
Este ejemplo ilustra que el coeficiente de correlación es inútil como medida de fuerza si la relación no es lineal. También ilustra una regla importante: Hacer siempre un gráfico de dispersión de los datos antes de calcular e interpretar el significado de r.

¿Por qué debemos hacer primero un gráfico de dispersión? Si no miráramos el diagrama de dispersión, sino que nos fijáramos sólo en r, ¿qué error podríamos cometer? Podríamos concluir que la relación entre las variables es débil (o que no hay relación) porque r es cercana a cero. Pero esta conclusión es errónea. Hemos interpretado erróneamente «r cercano a 0» como un indicador de una relación débil o de ausencia de relación, en lugar de una relación lineal débil o de ausencia de relación lineal. Podemos evitar fácilmente esta interpretación errónea de r observando el gráfico de dispersión.

Resumamos. Si r está cerca de cero, significa que los datos tienen una relación lineal muy débil o ninguna relación lineal. Cuando r está cerca de cero, es posible que los datos tengan una relación curvilínea fuerte (como vimos en este ejemplo). Para evitar errores, debemos mirar la forma de los datos en el diagrama de dispersión antes de calcular e interpretar r. Si la forma no es lineal, no utilice r.

3. La correlación por sí misma no es suficiente para determinar si una relación es lineal. Para ver esto, veamos una situación con un valor de r que se acerca a 1 pero una relación que no es lineal. Recordemos el estudio en el que se pagó a los participantes para que completaran una encuesta. El estudio examinó la relación entre la cantidad del incentivo monetario y el porcentaje de la muestra que devolvió la encuesta.

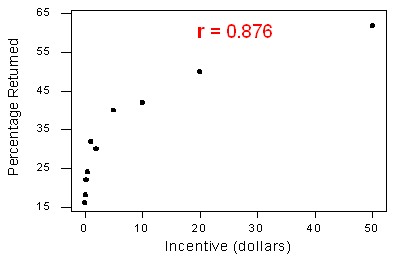
Las variables tienen una fuerte relación curvilínea, sin embargo la correlación es r = 0.876, bastante cercana a 1.

Revisando los dos últimos ejemplos, vemos que las relaciones curvilíneas fuertes pueden tener una correlación cercana a 0 o cercana a 1. Así que la correlación por sí sola no nos dice si una relación es lineal. Debemos mirar un gráfico de dispersión de los datos.

¡Siempre mira los datos!