El centro de gravedad es una propiedad geométrica de cualquier objeto.El centro de gravedad es el lugar medio del peso de un objeto. Podemos describir completamente el movimiento de cualquier objeto a través del espacio en términos de la traslación del centro de gravedad del objeto de un lugar a otro, y la rotación del objeto alrededor de su centro de gravedad si es libre de rotar. Si el objeto está confinado a girar alrededor de algún otro punto, como una bisagra, aún podemos describir su movimiento.En el vuelo, tanto los aviones como los cohetes giran alrededor de sus centros de gravedad.Una cometa, por otro lado, gira alrededor del punto de la brida.Pero el borde de una cometa aún depende de la ubicación del centro de gravedad en relación con el punto de la brida, porque para cada objeto el peso siempre actúa a través del centro de gravedad.
Determinar el centro de gravedad es muy importante para cualquier objeto volador.¿Cómo determinan los ingenieros la ubicación del centro de gravedad para un avión que están diseñando?
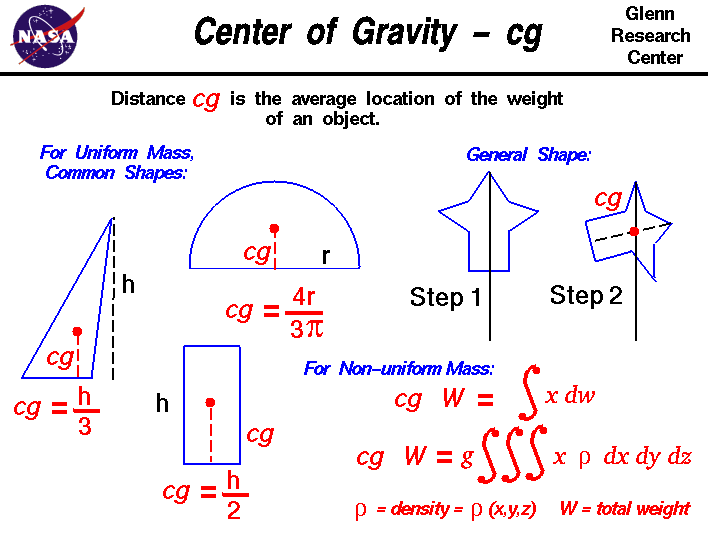
En general, determinar el centro de gravedad (cg) es un procedimiento complicado porque la masa (y el peso) pueden no estar distribuidos uniformemente por todo el objeto. Si la masa está distribuida uniformemente, el problema se simplifica en gran medida. Si el objeto tiene una línea (o plano) de simetría, el cg se encuentra en la línea de simetría. Para un bloque sólido de material uniforme, el centro de gravedad se encuentra simplemente en la ubicación media de las dimensiones físicas. (Para un bloque rectangular, 50 X 20 X 10, el centro de gravedad está en el punto (25,10, 5) ).Para un triángulo de altura h, el cg está en h/3, y para un semicírculo de radior, el cg está en (4*r/(3*pi)) donde pi es la relación entre la circunferencia del círculo y el diámetro. En los libros de matemáticas y ciencias existen tablas con la ubicación del centro de gravedad de muchas formas sencillas. Las tablas se generaron utilizando la ecuación de cálculo que se muestra en la diapositiva.
Para un objeto de forma general, hay una forma mecánica sencilla de determinar el centro de gravedad:
- Si simplemente equilibramos el objeto utilizando una cuerda o un borde, el punto en el que el objeto está equilibrado es el centro de gravedad. (¡Igual que equilibrar un lápiz en el dedo!)
- Otra forma, más complicada, es un método de dos pasos que se muestra en la diapositiva. En el paso 1, cuelgas el objeto de un punto cualquiera y dejas caer una cuerda con peso desde el mismo punto. Dibuja una línea en el objeto a lo largo de la cuerda. Para el paso 2, repite el procedimiento desde otro punto del objeto. Ahora tienes dos líneas dibujadas en el objeto que se cruzan. El centro de gravedad es el punto de intersección de las líneas. Este procedimiento funciona bien para los objetos de forma irregular que son difíciles de equilibrar.
- Si la masa del objeto no está distribuida uniformemente, debemos utilizar el cálculopara determinar el centro de gravedad.Utilizaremos el símbolo S dw para denotar la integración de una función continua con respecto al peso. Entonces el centro de gravedad se puede determinar a partir de:
cg * W = S x dw
donde x es la distancia desde una línea de referencia, dw es unincremento del peso, yW es el peso total del objeto. Para evaluar el lado derecho, tenemos que determinar cómo varía el pesogeométricamente. A partir de la ecuación del peso, sabemos que:
w = m * g
donde m es la masa del objeto, y g es la constante gravitatoria. A su vez, la masa m de cualquier objeto es igual a la densidad, rho,del objeto por el volumen, V:
m = rho * V
Podemos combinar las dos últimas ecuaciones:
w = g * rho * V
entonces
dw = g * rho * dV
dw = g * rho(x,y,z) * dx dy dz
Si tenemos una forma funcional para la distribución de la masa, podemos resolver la ecuación para el centro de gravedad:
cg * W = g * SSS x * rho(x,y,z) dx dy dz
donde SSS indica una integral triple sobre dx. dy. y dz.Si no conocemos la forma funcional de la distribución de masas,podemos integrar numéricamente la ecuación utilizando una hoja de cálculo.Dividir la distancia en un número de pequeños segmentos de volumen ydeterminar el valor medio del peso/volumen (densidad por gravedad) sobre ese pequeño segmento. La suma del valor medio del peso/volumen por la distancia y el segmento de volumen dividido por el peso dará como resultado el centro de gravedad.
Puedes ver un cortometraje de «Orville y Wilbur Wright» que explica cómo el centro de gravedad afectó al vuelo de su avión. El archivo de la película puede guardarse en su ordenador y verse como un Podcast en su reproductor de podcasts.
Actividades:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Visitas guiadas
-
 Peso del avión:
Peso del avión: 
-
 Fuselaje:
Fuselaje: 
Navegación .
![]()
![]()
![]()
![]()
![]()
Página principal de la Guía para principiantes