17.2 Conducción y convección combinadas

Siguiente: 17.3 Números adimensionales y Up: 17. Transferencia de calor convectiva Previous: 17.1 La analogía de Reynolds Contents Index

Ahora podemos analizar problemas en los que ocurren tanto conducción como convección, comenzando con una pared enfriada por un fluido que fluye a cada lado. Como se ha discutido, una descripción de la transferencia de calor por convección puede darse explícitamente como

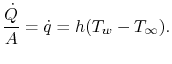
$\displaystyle \frac{dot{Q}{A}=\dot{q} = h(T_w-T_infty).$

Esto podría representar un modelo de un álabe de turbina con refrigeración interna. La figura 17.6 muestra la configuración.

Figura 17.6:Pared conductora con transferencia de calor por convección

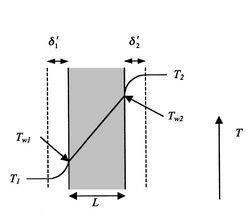
La transferencia de calor en el fluido 1 viene dada por

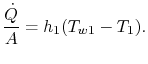
$\displaystyle \frac{dot{Q}{A} = h_1(T_{w1}-T_1).$

que es la transferencia de calor por unidad de superficie al fluido. La transferencia de calor en el fluido 2 viene dada de forma similar por

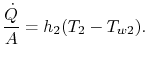
$\displaystyle \frac{dot{Q}{A} = h_2 (T_2 -T_{w2}).$

Al otro lado de la pared, tenemos

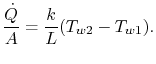$$\displaystyle \frac{dot{Q}{A} = \frac{k}{L}(T_{w2} -T_{w1}).La cantidad$ $ \dot{Q}/A$

es la misma en todas estas expresiones.Poniéndolas todas juntas para escribir la caída de temperatura global conocida se obtiene una relación entre la transferencia de calor y la caída de temperatura global, :

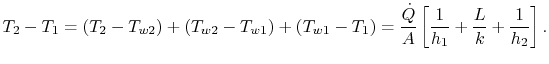$\displaystyle T_2-T_1 = (T_2-T_{w2})+(T_{w2}-T_{w1})+(T_{w1}-T_1) =\frac{\dot{Q}{A}left.$

(17..20)

Podemos definir una resistencia térmica,

, como antes, tal que

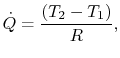
$\displaystyle \dot{Q} =\frac{(T_2 -T_1)}{R},$

donde viene dado por

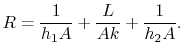$\displaystyle R = \frac{1}{h_1A} + \frac{L}{Ak} + \frac{1}{h_2A}.$

(17..21)

La ecuación (17.21) es la resistencia térmica para una pared sólida con transferencia de calor por convección en cada lado.

Para un álabe de turbina en un motor de turbina de gas, la refrigeración es una consideración crítica. En términos de la figura 17.6, es la temperatura de salida de la cámara de combustión (entrada de la turbina) y es la temperatura a la salida del compresor. Queremos encontrar $T_{w2}$ porque es la temperatura más alta del metal. A partir de(17.20), la temperatura de la pared se puede escribir como

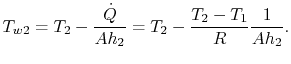$\displaystyle T_{w2} = T_2 - \frac{\dot{Q}{Ah_2}= T_2 - \frac{T_2 - T_1}{R}\frac{1}{Ah_2}.$

(17..22)

Utilizando la expresión de la resistencia térmica, las temperaturas de la pared pueden expresarse en términos de coeficientes de transferencia de calor y propiedades de la pared como

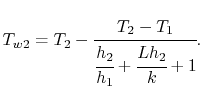$\displaystyle T_{w2} = T_2 - \cfrac{T_2 - T_1}{\cfrac{h_2}{h_1}+\cfrac{Lh_2}{k}+1}.$

(17..23)

La ecuación (17.23) proporciona algunas pautas básicas de diseño. El objetivo es tener un valor bajo de $T_{w2}$ . Esto significa que debe ser grande, debe ser grande (pero puede que no tengamos mucha flexibilidad en la elección del material) y debe ser pequeño. Una forma de conseguir lo primero es tener bajo (por ejemplo, hacer fluir aire de refrigeración hacia fuera como en laFigura 17.1 para proteger la superficie).

Un segundo ejemplo de conducción y convección combinadas viene dado por un cilindro expuesto a un fluido que fluye. La geometría se muestra en laFigura 17.7.

Figura 17.7:Cilindro en un fluido que fluye

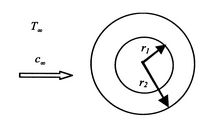
Para el cilindro el flujo de calor en la superficie exterior viene dado por

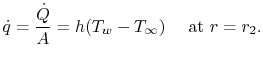$$\displaystyle \dot{q} = \frac{dot{Q}{A} = h(T_w-T_\infty)\Ncuadrado \textrm{en}r=r_2.La condición de contorno en la superficie interior puede ser una condición de flujo de calor o una especificación de temperatura; utilizamos esta última para simplificar el álgebra. Así,$ $ T = T_1$

en . Se trata de un modelo para la transferencia de calor en un tubo de radio rodeado por un aislamiento de espesor . La solución para una región cilíndrica se dio en la sección 16.5.1 como

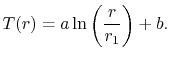
$\displaystyle T(r) =a\ln\left(\frac{r}{r_1}\right) +b.$

El uso de la condición de contorno produce .

En la interfase entre el cilindro y el fluido, , la temperatura y el flujo de calor son continuos. (Pregunta: ¿Por qué es esto? ¿Cómo argumentarías el punto?)

$$\ndisplaystyle \q} = \\ ~subbrace{-k\frac{dT}{dr}}{{substack{textrm{calor fl......2}{r_1}{right)+T_1{right)-T_\infty{right]}$

(17..24)

Colocando la forma de la distribución de temperatura en el cilindroen la Ecuación (17.24) yields

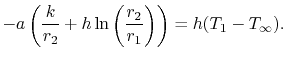
$\displaystyle -a\left(\frac{k}{r_2}+h\ln\left(\frac{r_2}{r_1}\right)\right)=h(T_1-T_\infty).$

La constante de integración, , es

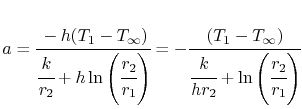
$\displaystyle a=\cfrac{-h(T_1-T_infty)}{cfrac{k}{r_2}+h\ln\left(\cfrac{r_2}{r......t)}=-\cfrac{(T_1-T_infty)}{cfrac{k}{hr_2}+\ln\left(\cfrac{r_2}{r_1}\right)}$

y la expresión para la temperatura es, en forma normalizada no dimensional,

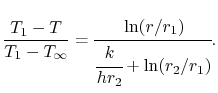$\displaystyle \frac{T_1-T}{T_1-T_infty} = \cfrac{ln(r/r_1)}{cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..25)

El flujo de calor por unidad de longitud, $\dot{Q}$ , viene dado por

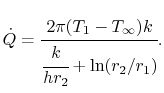$\displaystyle \dot{Q}=\cfrac{2\pi(T_1-T_infty)k}{cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..26)

Las unidades de la ecuación (17.26) son W/m-s.

Un problema de interés es elegir el espesor del aislamiento para minimizar la pérdida de calor para una diferencia de temperatura fija $T_1-T_\infty$ entre el interior de la tubería y el fluido que fluye lejos de la misma. ( $T_1-T_\infty$ es la distribución de la temperatura de conducción para la tubería). Para comprender el comportamiento de la transferencia de calor, examinamos el denominador de la ecuación (17.26) a medida que varía . El espesor del aislamiento que proporciona la máxima transferencia de calor viene dado por

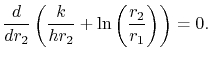$\displaystyle \frac{d}{dr_2}\left(\frac{k}{hr_2}+\ln\left(\frac{r_2}{r_1}\right)\right)=0.$

(17..27)

(Pregunta: ¿Cómo sabemos que es un máximo?)

De la ecuación (17.27), el valor de para el máximo $\dot{Q}$ es, pues,

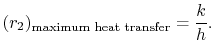$\displaystyle (r_2)_{textrm{máxima transferencia de calor}} = \frac{k}{h}.$

(17..28)

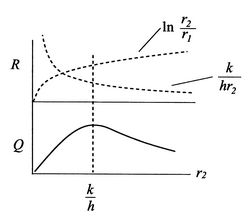
Si es menor que esto, podemos añadir aislamiento y aumentar la pérdida de calor. Para entender por qué ocurre esto, considera laFigura 17.8, que muestra un esquema de la resistencia térmica y la transferencia de calor. A medida que aumenta desde un valor inferior a , se producen dos efectos. En primer lugar, el grosor del aislamiento aumenta, lo que tiende a reducir la transferencia de calor porque el gradiente de temperatura disminuye; en segundo lugar, el área de la superficie exterior del aislamiento aumenta, lo que tiende a incrementar la transferencia de calor. El segundo está asociado (vagamente) al término , el primero al término $\ln(r_2/r_1)$ . Por tanto, hay dos efectos que compiten entre sí y que se combinan para dar un máximo $\dot{Q}$ en .