Wenn ein Gas durch ein Rohr gepresst wird, werden die Gasmoleküle von den Wänden des Rohrs abgelenkt. Wenn die Geschwindigkeit des Gases viel geringer ist als die Schallgeschwindigkeit des Gases, bleibt die Dichte des Gases konstant und die Geschwindigkeit der Strömung nimmt zu.Wenn sich die Geschwindigkeit der Strömung jedoch der Schallgeschwindigkeit nähert, müssen wir die Kompressibilitätseffekte des Gases berücksichtigen. Die Dichte des Gases variiert von einer Stelle zur nächsten. Wenn die Strömung durch ein Rohr, wie in der Abbildung gezeigt, sehr allmählich komprimiert (Fläche nimmt ab) und dann allmählich expandiert (Fläche nimmt zu) wird, kehren die Strömungsbedingungen zu ihren ursprünglichen Werten zurück. Aus der Betrachtung des zweiten Hauptsatzes der Thermodynamik ergibt sich, dass eine reversible Strömung einen konstanten Wert der Entropie beibehält.
Ingenieure bezeichnen diese Art von Strömung als isentrope Strömung; eine Kombination aus dem griechischen Wort „iso“ (gleich) und Entropie.
Isentrope Strömungen treten auf, wenn die Änderung der Strömungsgrößen klein und allmählich ist, wie z. B. bei der oben gezeigten idealen Strömung durch die Düsen.
Die Erzeugung von Schallwellen ist ein isentroper Prozess. Die Erzeugung von Schallwellen ist ein isentroper Vorgang.
Eine Überschallströmung, die bei zunehmender Strömungsfläche gedreht wird, ist ebenfalls isentrop.
Wir nennen dies wegen der Flächenvergrößerung eine isentrope Expansion.
Wird eine Überschallströmung abrupt gedreht und nimmt die Strömungsfläche ab, werden Schockwellen erzeugt und die Strömung ist irreversibel.
Die isentropen Beziehungen sind nicht mehr gültig und die Strömung wird von den schrägen oder normalen Schockbeziehungen beherrscht.
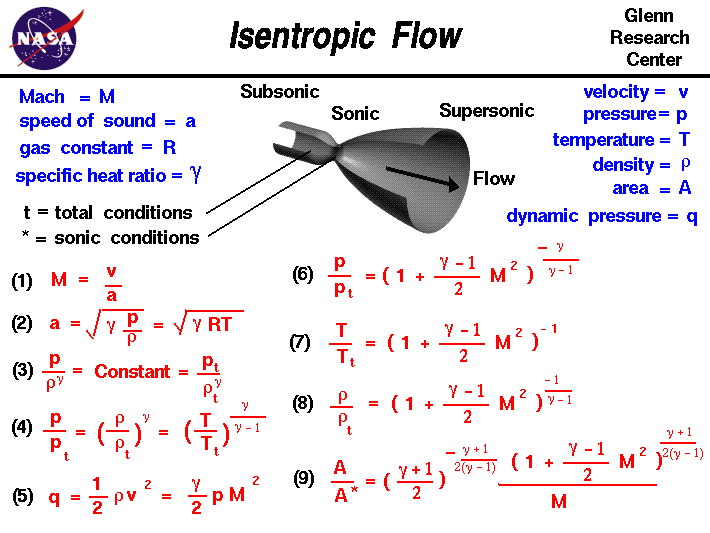
Auf dieser Folie haben wir viele der wichtigen Gleichungen gesammelt, die eine isentrope Strömung beschreiben. Wir beginnen mit der Definition der Machzahl, da dieser Parameter in vielen Gleichungen der isentropen Strömung vorkommt.
Die Machzahl M ist das Verhältnis der Strömungsgeschwindigkeit v zur Schallgeschwindigkeit a.
Gleichung 1:
Die Schallgeschwindigkeit hängt wiederum von der Dichte r, dem Druck p, der Temperatur T und dem Verhältnis der spezifischen Wärme gam ab:
Gleichung #2:
wobei R die Gaskonstante aus den Zustandsgleichungen ist. Wenn wir mit den Entropiegleichungen für ein Gas beginnen, kann gezeigt werden, dass Druck und Dichte einer isentropen Strömung wie folgt zusammenhängen:
Gleichung #3:
Wir können den Wert der Konstante bestimmen, indem wir die Gesamtbedingungen als Druck und Dichte definieren, wenn die Strömung isentrop zur Ruhe gebracht wird.Das tiefgestellte „t“, das in vielen dieser Gleichungen verwendet wird, steht für „totalconditions“. (Sie haben wahrscheinlich bereits eine Vorstellung von den totalen Bedingungen aus der Erfahrung mit der Bernoulli-Gleichung).
Gleichung (3):
Mit Hilfe der Zustandsgleichung können wir aus Gleichung (3) leicht die folgenden Beziehungen ableiten:
Gleichung #4:
Der dynamische Druck q ist definiert als:
Gleichung #5:
Unter Verwendung der Massen-, Impuls- und Energieerhaltung und der Definition der Gesamtenthalpie in der Strömung können wir die folgenden Beziehungen ableiten:
Gleichung #6:
Gleichung #7:
Gleichung #8:
Betrachten wir dann die kompressible Massenflussgleichung.können wir ableiten:
Gleichung #9:
Die starren Bedingungen treten auf, wenn die Strömung gedrosselt ist und die Machzahl gleich eins ist.Beachten Sie die wichtige Rolle, die die Machzahl in allen Gleichungen auf der rechten Seite dieser Folie spielt. Wenn die Machzahl der Strömung bestimmt ist, können alle anderen Strömungsbeziehungen bestimmt werden. In ähnlicher Weise wird durch die Bestimmung einer beliebigen Strömungsbeziehung (z. B. Druckverhältnis) die Machzahl festgelegt und alle anderen Strömungsbedingungen bestimmt.
Hier ist ein JavaScript-Programm, das die Gleichungen auf dieser Folie löst.
Berechnen
Sie wählen eine Eingangsvariable aus, indem Sie die Auswahltaste mit der Bezeichnung InputVariable benutzen. Neben der Auswahl geben Sie dann den Wert der gewählten Variable ein. Wenn Sie den roten COMPUTE-Button drücken, ändern sich die Ausgangswerte. Einige der Variablen (z. B. das Flächenverhältnis) sind doppelwertig. Das bedeutet, dass es für dasselbe Flächenverhältnis eine Unterschall- und eine Überschalllösung gibt. Die Variable „Wcor/A“ ist die aus dem kompressiblen Massenstrom ableitbare Funktion des korrigierten Luftstroms pro Flächeneinheit, die nur von der Machzahl der Strömung abhängig ist. Diese zusätzlichen Größen werden bei der Auslegung von Hochgeschwindigkeitseinlässen, Düsen und Kanälen verwendet.
Wenn Sie ein erfahrener Benutzer dieses Rechners sind, können Sie eine abgespeckte Version des Programms verwenden, die schneller auf Ihren Computer geladen wird und diese Anweisungen nicht enthält.Sie können auch Ihre eigene Kopie des Programms herunterladen, um es offline auszuführen, indem Sie auf diese Schaltfläche klicken:
![]()
Aktivitäten:
Führungen
-
 Kompressible Aerodynamik:
Kompressible Aerodynamik: 
-
 Schallwellen:
Schallwellen: 
-
 Isentrope Strömungsberechnung:
Isentrope Strömungsberechnung: 
-
 Düsensimulator:
Düsensimulator: 
Navigation …
![]()
![]()
![]()
![]()
![]()
Anfängerhandbuch Startseite