Mit einer Korrelations- oder einfachen linearen Regressionsanalyse kann festgestellt werden, ob zwei numerische Variablen in einem signifikanten linearen Zusammenhang stehen. Eine Korrelationsanalyse liefert Informationen über die Stärke und Richtung der linearen Beziehung zwischen zwei Variablen, während eine einfache lineare Regressionsanalyse Parameter in einer linearen Gleichung schätzt, die zur Vorhersage von Werten einer Variablen auf der Grundlage der anderen verwendet werden kann.
Korrelation
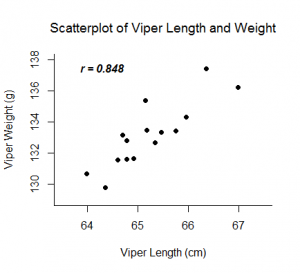
Der Pearson-Korrelationskoeffizient, r, kann Werte zwischen -1 und 1 annehmen. Je weiter r von Null entfernt ist, desto stärker ist die lineare Beziehung zwischen den beiden Variablen. Das Vorzeichen von r entspricht der Richtung des Zusammenhangs. Wenn r positiv ist, steigt mit dem Anstieg der einen Variable auch die andere. Wenn r negativ ist, dann nimmt die andere Variable tendenziell ab, wenn eine Variable zunimmt. Eine perfekte lineare Beziehung (r=-1 oder r=1) bedeutet, dass eine der Variablen perfekt durch eine lineare Funktion der anderen erklärt werden kann.
Beispiele:

Lineare Regression
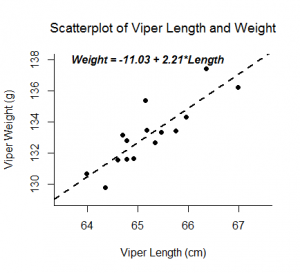
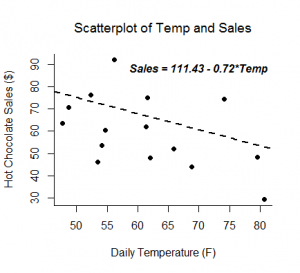
Eine lineare Regressionsanalyse liefert Schätzungen für die Steigung und den Achsenabschnitt der linearen Gleichung, die eine Ergebnisvariable, Y, basierend auf den Werten einer Prädiktorvariable, X, vorhersagt. Eine allgemeine Form dieser Gleichung ist unten dargestellt:
![]()
Der Achsenabschnitt, b0, ist der vorhergesagte Wert von Y, wenn X=0 ist. Die Steigung, b1, ist die durchschnittliche Änderung von Y für jede Erhöhung von X um eine Einheit. Die Steigungsschätzung gibt nicht nur die Stärke und Richtung der linearen Beziehung zwischen X und Y an, sondern erlaubt auch eine Interpretation, wie sich Y ändert, wenn X zunimmt. Diese Gleichung kann auch verwendet werden, um Werte von Y für einen Wert von X vorherzusagen.
Beispiele:
Inferenz
Inferenztests können sowohl für die Korrelations- als auch für die Steigungsschätzungen durchgeführt werden, die aus einer Stichprobe einer Population berechnet wurden. Beide Analysen sind t-Tests, die auf die Nullhypothese ausgeführt werden, dass die beiden Variablen nicht linear miteinander verbunden sind. Wenn ein Korrelationstest und ein Steigungstest mit denselben Daten durchgeführt werden, liefern sie dieselbe Teststatistik und denselben p-Wert.
Annahmen:
- Stichproben
- Independente Beobachtungen
- Die Prädiktorvariable und die Ergebnisvariable stehen in einem linearen Verhältnis zueinander (beurteilt durch visuelle Überprüfung eines Streudiagramms).
- Die Grundgesamtheit der Werte für das Ergebnis ist für jeden Wert des Prädiktors normalverteilt (beurteilt durch Bestätigung der Normalität der Residuen).
- Die Varianz der Verteilung des Ergebnisses ist für alle Werte des Prädiktors gleich (beurteilt durch visuelle Überprüfung eines Residuenplots auf ein Trichtermuster).
Hypothesen:
Ho: Die beiden Variablen sind nicht linear miteinander verbunden.
Ha: Die beiden Variablen stehen in einem linearen Zusammenhang.
Relevante Gleichungen:
Freiheitsgrade: df = n-2


![]()
Beispiel 1: Handberechnung
In diesen Videos wird der lineare Zusammenhang zwischen der Körpergröße von Personen und der Messung der Armspannweite untersucht.
Korrelation:


Regression:


Fazit: Bei der Untersuchung des Zusammenhangs zwischen Armspanne und Körpergröße finden wir eine große positive Korrelation (r=.95), was auf einen starken positiven linearen Zusammenhang zwischen den beiden Variablen hinweist. Wir haben die Gleichung für die beste Anpassungslinie als Armspanne=-1,27+1,01(Höhe) berechnet. Dies bedeutet, dass für eine Person, die null Zoll groß ist, die vorhergesagte Armspanne -1,27 Zoll betragen würde. Dies ist kein möglicher Wert, da der Bereich unserer Daten viel höher liegen wird. Für jede Zunahme der Körpergröße um 1 Zoll wird eine Zunahme der Armspanne um 1,01 Zoll vorhergesagt.
Beispiel 2: Durchführen der Analyse in Excel 2016
Für einen Teil dieser Analyse müssen Sie das Add-in Data Analysis ToolPak in Excel aktiviert haben. Anweisungen zur Durchführung dieser Analyse in früheren Versionen von Excel finden Sie unter https://stat.utexas.edu/videos
Datensatz, der in den Videos verwendet wird
Korrelationsmatrix und p-Wert:
PDF-Richtungen entsprechend dem Video

Streudiagramme erstellen:
PDF-Anleitung entsprechend dem Video
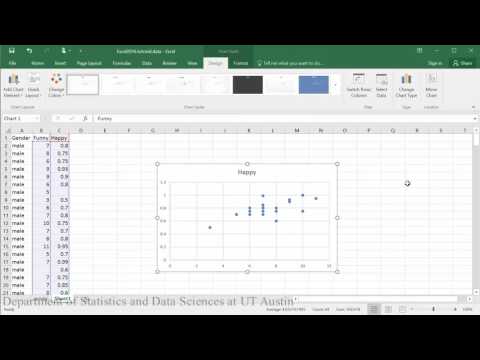

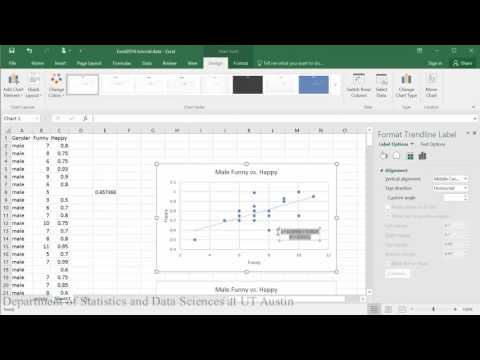
Lineares Modell (erste Hälfte des Tutorials):
PDF-Anleitung zum Video

Erstellen von Residuenplots:
PDF-Anleitung zum Video
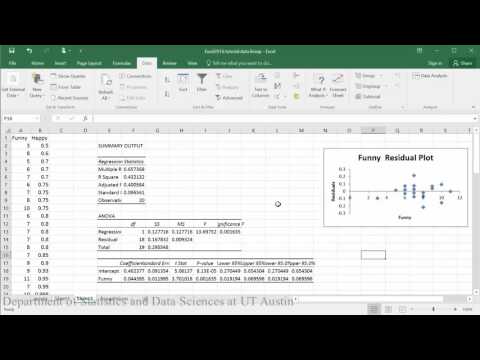

Beispielhafte Schlussfolgerung: Bei der Auswertung des Zusammenhangs zwischen der Frage, wie glücklich jemand ist und wie lustig andere ihn bewerten, zeigt das Streudiagramm, dass es einen mäßig starken positiven linearen Zusammenhang zwischen den beiden Variablen zu geben scheint, was durch den Korrelationskoeffizienten (r = .65) unterstützt wird. Eine Überprüfung der Annahmen anhand des Residuenplots zeigte keine Probleme mit den Daten. Die lineare Gleichung für die Vorhersage von Happy aus Funny lautete Happy=.04+0.46(Funny). Der y-Achsenabschnitt zeigt an, dass für eine Person, deren Lustigkeitsbewertung Null war, ihr Glücklichsein mit 0,04 vorhergesagt wird. Das Funny-Rating sagt das Glück signifikant voraus, so dass für jede Erhöhung des Funny-Ratings um 1 Punkt eine Erhöhung des Glücks um .46 vorhergesagt wird (t = 3.70, p = .002).
Beispiel 3: Durchführung der Analyse in R
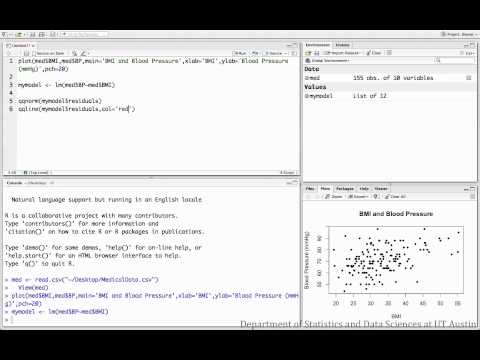
Die folgenden Videos untersuchen den Zusammenhang zwischen BMI und Blutdruck für eine Stichprobe von medizinischen Patienten.
Datensatz, der in den Videos verwendet wird
Korrelation:
R-Skriptdatei, die im Video verwendet wird

Regression:
R-Skriptdatei, die im Video verwendet wird