MRI Physics: Diffusionsgewichtete Bildgebung

Moleküle im Gewebe sind nicht an ihrem Platz fixiert, sondern bewegen sich mit der Zeit. Ein Teil dieser Bewegung steht im Zusammenhang mit aktiven Prozessen, wie z.B. der Blutzirkulation, während ein anderer Teil der Bewegung einfach eine zufällige Bewegung ohne Nettoziel ist. Dieses letztere Phänomen hängt mit der Wärme (Energie) im Gewebe zusammen und wird als Brownsche Bewegung bezeichnet. Wie bereits erwähnt, gibt es keine Netto-Flussrichtung – die Moleküle werden in der Lösung einfach geschüttelt und springen umher, bewegen sich auf einem zufälligen, mäandernden Pfad und ändern ihre Richtung, wenn sie auf andere Moleküle stoßen. Die Bewegung der Moleküle über die Zeit wird als molekulare Diffusion bezeichnet.

Die Bewegung dieser Wassermoleküle kann durch das Vorhandensein von Barrieren, vor allem Zellmembranen, eingeschränkt werden. Eine Illustration dieses Prozesses sehen Sie unten. Der Grad der Diffusionsbeschränkung kann durch einen Diffusionskoeffizienten quantifiziert werden, der die durchschnittliche Entfernung widerspiegelt, die ein Teilchen in einer Sekunde zurücklegt; der tatsächliche Diffusionskoeffizient ist normalerweise nicht wichtig, aber er ist für die Terminologie nützlich.

Freies Wasser	Intrazelluläres Wasser
	Ihr Browser unterstützt den HTML-Canvas nicht.	Ihr Browser unterstützt den HTML-Canvas nicht.

Illustration der Brownschen Bewegung; links, freie Wasserdiffusion und rechts, durch eine Zellmembran eingeschränkte Bewegung. Führen Sie die Simulation mehrmals durch, um zu sehen, wie die Wege durch die Zelle eingeschränkt werden. Die rote Linie markiert den Weg des Moleküls, während die graue Linie die Nettoverschiebung am Ende des Durchlaufs anzeigt.

Wie Sie sich vorstellen können, wirken sich Änderungen in der Zelldichte des Gewebes und der Menge an intrazellulärem gegenüber extrazellulärem Wasser auf den Grad der Diffusionsbeschränkung in diesem Gewebevolumen aus. Zustände wie ischämische Infarkte im Gehirn, eitrige Abszesse und kleine, runde Blauzellentumore neigen zu einer starken Einschränkung der Diffusion; Zysten und Ödeme weisen einen geringen Grad an Diffusionseinschränkung auf.

Diffusionsgewichtete Bildgebung

Diffusionsgradienten. Die Fähigkeit, die Diffusionskoeffizienten innerhalb eines Organs zu messen und zu vergleichen, ist für eine wachsende Zahl von Anwendungen wichtig, wie z. B. für die Beurteilung eines akuten Schlaganfalls. Eine MR-Pulssequenz kann so gestaltet werden, dass sie empfindlich auf die Molekulardiffusion reagiert, wobei ähnliche Konzepte wie bei der flussbezogenen Dephasierung und der Phasenkontrast-MRA zum Einsatz kommen.

Insbesondere werden Partikel, die sich zwischen der Anwendung zweier räumlicher Gradientenpulse bewegen, unterschiedliche Gradientenstärken erfahren (da sie sich an unterschiedlichen Positionen befinden).

Erinnern Sie sich daran, dass die Anwendung eines Gradientenpulses eine Phasenverschiebung in der Protonenpräzession induziert; um dieses Konzept zu überprüfen, können Sie den Abschnitt über die Phasencodierung für die räumliche Lokalisierung lesen. Wenn wir einen Gradienten anlegen und ihn dann genau umkehren, erfahren Teilchen, die sich an der gleichen Stelle befinden, keine Netto-Phasenverschiebung, während Teilchen, die sich bewegt haben, eine Phasenverschiebung erfahren.

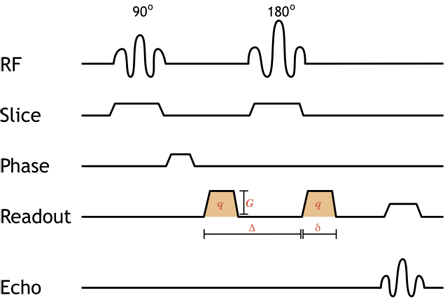
Vereinfachtes Pulsdiagramm einer diffusionsgewichteten Spin-Echo-Bildsequenz. Die orange schattierten Gradienten sind die Diffusionsgradienten (man beachte, dass beide positiv sind, da der 180-Grad-Puls dazwischen die Präzessionsrichtung umkehrt, so dass der zweite eigentlich negativ ist). Das Hinzufügen von gleichen, gepaarten Diffusionsgradienten zur Standard-Spin-Echo-Sequenz bewirkt, dass sich bewegende Protonen dephasieren. Der Grad der Diffusionsgewichtung hängt von der Stärke des Gradienten (Amplitude G und Dauer δ) sowie dem zeitlichen Abstand zwischen ihnen (Δ) ab – dies wird als b-Wert bezeichnet, der weiter unten besprochen wird.

Ihr Browser unterstützt den HTML-Canvas nicht.

Illustration der Gradienten, die für die diffusionsgewichtete Bildgebung verwendet werden. In der oberen Hälfte des Bildes sind zwei graue stationäre Protonen dargestellt, in der unteren Hälfte zwei blaue bewegliche Protonen. Der Diffusionsgradient (der entlang der x-Achse variiert) ist unten in rot dargestellt, wenn er eingeschaltet ist. Für die stationären Protonen ist zu beachten, dass sie zu Beginn der Pulssequenz synchronisiert sind, mit dem Gradienten dephasieren und dann wieder in Phase gehen, wenn der Gradient umgekehrt wird. Die mobilen Protonen können sich jedoch nicht umphasieren, da sie sich bewegt haben – sie erfahren nicht die gleiche Gradientenstärke wie zu Beginn.

Diese Protonen akkumulieren ungleiche Phasenverschiebungen, und das Nettosignal wird verringert (Dephasierung).

b-Wert. Für ein diffusionsgewichtetes Bild können wir das Ausmaß der DWI-Gewichtung ändern, das wir wollen, d. h. was unser „Schwellenwert“ für die Diffusionseinschränkung ist.

Indem wir den Zeitabstand und die Stärke der Diffusionsgradienten anpassen, können wir das Bild mehr oder weniger empfindlich für molekulare Bewegungen machen. Eine Vergrößerung des Gradienten oder eine Erhöhung des zeitlichen Abstands zwischen den Dephasierungs- und Rephasierungsgradienten führt zu einer wesentlich stärkeren Dephasierung bei gleichem Ausmaß der Brownschen Bewegung. Der Grad der DWI-Gewichtung wird als b-Wert bezeichnet (quantitativ: b ∝ q2 * Δ , wobei q die Gradientenstärke und Δ die Zeit zwischen den beiden Gradienten ist). Bilder mit niedrigem b-Wert werden nur geringfügig durch die Diffusionseigenschaften des Gewebes beeinflusst.Ein höherer b-Wert ergibt insgesamt ein dunkleres Bild, da die meisten Gewebe das Signal durch die molekulare Bewegung verlieren – aber begrenzte Läsionen werden auffälliger sein;typischerweise werden wir aus den unten besprochenen Gründen mehrere b-Werte erfassen, um ein ADC-Bild zu berechnen. Siehe unten für eine Simulation, die diesen Punkt veranschaulicht.

DWI-Impulssequenz. Wir können nun praktische Details diskutieren – wie akquiriert man ein diffusionsgewichtetes Bild? Typische DWI-Sequenzen sind Spin-Echosequenzen, mit 90- und 180-Grad-Pulsen. (Es werden neuere Methoden zur Durchführung von DWI entwickelt, die nicht alle Spin-Echo-Sequenzen verwenden.) Die Diffusionsgradienten werden vor und nach dem 180-Grad-Puls eingeschaltet (es sind also beide positive Gradienten, weil der 180-Grad-Puls dazu dient, die Wirkung des zweiten Pulses umzukehren). DWI-Sequenzen müssen extrem schnell sein, um jede Bewegung innerhalb des Körperteils zu eliminieren – da der gesamte Zweck der DWI-Sequenz darin besteht, infinitesimale Bewegungen von Wassermolekülen zu messen, werden unsere Bilder durch makroskopische Bewegungen vollständig zerstört. Lange Zeit war die schnellste verfügbare Sequenz die echoplanare Bildgebung (EPI), und praktisch alle derzeit verwendeten DWI-Sequenzen verwenden EPI.

Im Grunde möchten wir, dass unsere DWI-Bilder vollständig „DWI-gewichtet“ sind – mit anderen Worten, wir möchten nur die Ergebnisse der Diffusion sehen, nicht aber andere Eigenschaften des Gewebes. Die TR ist lang, um T1-Effekte zu reduzieren und das Signal zu verbessern. Die TE wird so kurz wie möglich gehalten, aber die Einblendung des Diffusionsgradienten nach dem 180er-Puls erfordert eine längere TE; daher sind DWI-Bilder auch T2-gewichtet. Dies ist ein sehr wichtiger Punkt, der zu beachten ist – Läsionen können auf der DWI allein aufgrund von T2-Effekten hell sein (dies ist als T2-Shine-Through bekannt), und Läsionen mit eingeschränkter Diffusion und langer T2-Relaxation erscheinen sehr hell!

Fett. Fett bereitet in der DWI aus mehreren Gründen Probleme. Erstens ist es auf DWI-Bildern hell, weil sich Fettmoleküle nicht sehr viel bewegen (sie sind relativ eingeschränkt); das Fettsignal kann Läsionen verdecken. Zweitens wird das Artefakt der chemischen Verschiebung (der ersten Art) durch die echoplanare Bildgebung (EPI) stark vergrößert, oft um 10 Pixel einer Verschiebung! (Dies liegt daran, dass sich Phasenverschiebungen über die einzelne Aufnahme der EPI-Sequenz akkumulieren; eine technische Diskussion finden Sie in den Referenzen). Daher könnte Fett aus dem subkutanen Gewebe Läsionen im Gehirn oder in der Leber verdecken. Aus diesen beiden Gründen ist eine homogene Fettunterdrückung für DWI-Bilder notwendig.

Scheinbarer Diffusionskoeffizient

Wie oben beschrieben, sind DWI-Bilder von Natur aus T2-gewichtet. Daher erscheinen Läsionen mit langer T2-Relaxation hell, auch wenn sie die Diffusion nicht einschränken. Dieser Effekt wird besonders auf Bildern mit niedrigem b-Wert deutlich, bei denen die Diffusionsgewichtung geringer ist (d. h. Läsionen mit schneller Diffusion haben nicht viel Signal verloren und werden daher immer noch hell erscheinen). Freies Wasser (z. B. Liquor, Zysten) ist aufgrund seines extrem langen T2 auch auf relativ hohen b-Werten hell. Wir möchten die T2-Effekte eliminieren, um eine genauere Vorstellung von der Diffusionsbeschränkung zu erhalten und störende helle Flecken zu vermeiden. Um dies zu erreichen, können wir den Diffusionskoeffizienten tatsächlich berechnen, indem wir mehrere DWI-Serien mit unterschiedlichen b-Werten verwenden.

Scheinender Diffusionskoeffizient. Die Diffusionskoeffizienten, die wir im MRT messen, stellen Mittelwerte des gesamten Voxels und jeder Diffusionsrichtung dar (siehe Diskussion über Anisotropie und DTI später). Daher verwenden wir das Wort scheinbar, um die von uns berechneten Werte zu beschreiben. Das Signal eines bestimmten Gewebes nimmt mit zunehmendem b-Wert exponentiell ab. Bei einem scheinbaren Diffusionskoeffizienten D ist die Signalintensität I

I = I0 * e-b * D, wobei I0 von den T2-Eigenschaften abhängt

Wenn wir mindestens 2 DWI-Sequenzen mit unterschiedlichen b-Werten aufnehmen, können wir diese in die Gleichung einsetzen, um D zu lösen.z. B. 40, 400 und 800); wir können den Logarithmus der Intensität nehmen, um den Graphen zu linearisieren, und dann eine lineare Regression verwenden, um einen Best-Fit-D-Wert zu erhalten. Indem wir D für jedes Pixel auftragen, erhalten wir das ADC-Bild (manchmal ADC-Karte genannt).

DWI b-Wert:		ADC
	Ihr Browser unterstützt das HTML-Canvas nicht.	Ihr Browser unterstützt das HTML-Canvas nicht.	Ihr Browser unterstützt das HTML-Canvas nicht.

Simulation, wie sich unterschiedliche b-Werte auf das Erscheinungsbild von DWI-Bildern auswirken und wie man ADC berechnet. Links, simulierte DWI-Bilder mit hellem Liquor auf den Bildern mit niedrigem b-Wert und erhöhter Sichtbarkeit des linken frontalen Schlaganfalls auf den Bildern mit hohem b-Wert. Mitte, Darstellung des Logarithmus der Signalintensität verschiedener Gewebe (blau, Liquor; grau, Gehirn; braun, Schlaganfall) bei unterschiedlichen b-Werten. Die Steigung der Linie, die den Punkt verbindet, ist die ADC. Rechts, simuliertes ADC-Bild; Bereiche mit Diffusionseinschränkung, die die flachste Steigung auf dem mittleren Diagramm aufweisen, haben das dunkelste Signal auf dem ADC-Bild.

Bereiche mit Diffusionseinschränkung verlieren das geringste Signal auf Bildern mit hohen b-Werten (weil sich ihre Protonen nicht bewegen). Die Steigung der Linie auf dem DWI-Plot (siehe oben) wird flach sein, und somit wird der ADC-Wert klein sein (also dunkle Pixel). Andererseits verlieren Bereiche mit schneller Diffusion das meiste Signal, wenn die b-Werte steigen, was zu einer großen Steigung führt – und zu hellen Pixeln auf dem ADC-Bild. Wichtig ist, dass das T2-Shine-Through – d.h. die Helligkeit auf DWI-Bildern in Bezug auf das zugrunde liegende T2-Signal im Gewebe – nur die Anfangsposition der Punkte im DWI-Plot beeinflusst; es hat keinen Einfluss auf die Steigung, daher ist das ADC-Bild unabhängig vom T2-Shine-Through – es spiegelt allein die Diffusion wider.

Klinisch verwenden wir typischerweise immer noch DWI-Bilder, weil helle Anomalien viel leichter zu sehen sind als dunkle Anomalien (Sie können dies vielleicht in der obigen Simulation sehen). Man hat verschiedene Strategien entwickelt, um das ADC-Bild in eine „hell = schlecht“-Karte umzuwandeln; zum Beispiel nimmt die exponentielle ADC (EADC)-Karte den Exponentialwert der ADC-Werte, was zu einer invertierten Skala führt, die dem DWI ähnlicher ist (aber wiederum T2-Shine-Through-Effekte eliminiert). Ein weiterer wichtiger Grund für die Verwendung von DWI-Bildern ist, dass das ADC-Bild aufgrund der Tatsache, dass es auf mehreren DWI-Bildern basiert, von Natur aus anfälliger für Artefakte ist als einzelne DWI-Bilder. Schließlich sind viele Anomalien nicht nur diffusionseinschränkend, sondern auch hell auf T2; daher können wir den T2-Glanz-Effekt ausnutzen, um Läsionen auffälliger zu machen und dann die wahre Diffusionseinschränkung auf der ADC-Karte zu bestätigen.

Diffusion Tensor Imaging

Bislang hatten wir eine vereinfachte Sicht der Diffusion – dass Wassermoleküle in alle Richtungen gleichermaßen diffundieren können. Tatsächlich ist dies, zumindest in einigen Geweben, überhaupt nicht der Fall. In stark strukturierten Geweben, insbesondere in Nerven und Bahnen der weißen Substanz im Gehirn, erfolgt die Diffusion bevorzugt in eine Richtung: In der weißen Substanz umschließen Myelinscheiden die Neuronen und verhindern die Wasserdiffusion durch die Scheide, erlauben sie aber in Richtung der Axone. Diffusion, die richtungsabhängig ist, wird als anisotrop bezeichnet (d.h. nicht in jeder Richtung gleich). Das bedeutet, dass wir, wenn wir die Diffusion mit Gradienten in einer Richtung messen, eine andere Antwort erhalten, als wenn wir sie in einer anderen Richtung messen. Ebenso wichtig ist, dass wir, wenn wir die Diffusion in einer Richtung messen, unterschiedliche Antworten für verschiedene Teile derselben (gesunden) weißen Substanz erhalten, je nach der Richtung der Axone in jedem Teil.

Intuitiv wäre es naheliegend, dass die Lösung für dieses Problem darin besteht, die Diffusion in mehreren Richtungen zu messen und eine Art Mittelwert zu bilden – dies würde alle Richtungsverzerrungen ausgleichen. Die einfachste Methode, die Diffusion in verschiedenen Richtungen zu messen, nennt sich Diffusion Tensor Imaging (DTI).DTI geht davon aus, dass innerhalb jedes Voxels eine einzige Richtungsverzerrung vorliegt, z. B. eine einzige Richtung der Neuronenbündel. Es modelliert dann die Diffusion innerhalb eines Axons nicht als Skalar (einzelne Zahl), sondern als 3-dimensionales Ellipsoid, das als Tensor bezeichnet wird.

Illustration des Diffusionstensors. Dargestellt ist ein Bündel von Axonen (gelb) in 3 Dimensionen. Wassermoleküle können entlang der Axone diffundieren, aber nicht durch sie hindurch. Der Diffusionstensor (braun) stellt die Diffusion als Ellipsoid dar, das entlang der Axone orientiert ist, wobei die Dicke des Ellipsoids in jeder Richtung dem Diffusionskoeffizienten in dieser bestimmten Richtung entspricht. Die Ellipse hat also eine dünne Taille, da die ADC entlang der Axone niedrig ist, aber die Ellipse ist länglich, da die ADC entlang der Achse der Axone hoch ist.

Aus der obigen Abbildung können Sie ersehen, dass die Spezifizierung des Diffusionstensors zwei separate Parametersätze erfordert: die Richtung der schnellsten Diffusion (d.h. die Richtung des Axonbündels) und die tatsächlichen Diffusionskoeffizienten entlang und über die Axone. Eine Richtung im 3-dimensionalen Raum erfordert3 Zahlen; und die Dicke der Ellipse erfordert 3 Zahlen (für jede Achse der Ellipse selbst). Dies bedeutet, dass DTI die Messung der Diffusion in 6 verschiedenen Richtungen erfordert. (Diese Richtungen müssen für jeden b-Wert ungleich Null gemessen werden.)

DTI-Sequenzen sind notwendig, um gleichmäßige diffusionsgewichtete Bilder im Gehirn zu erzeugen – andernfalls würden die Trakte der weißen Substanz aussehen, als würden sie die Diffusion einschränken. Die mittleren Diffusionsbilder werden dann durch Mittelung von drei der Richtungen erzeugt, und das ist es, was typischerweise für DWI- und ADC-Karten verwendet wird.

Durch die Aufnahme der 6 verschiedenen Richtungen können wir jedoch auch andere Karten berechnen. Eine der gebräuchlichsten ist die Karte der fraktionierten Anisotropie (FA). Erinnern Sie sich daran, dass die Anisotropie den Grad darstellt, in dem die Diffusion nicht in allen Richtungen gleich ist; FA wird berechnet, indem die Längen der einzelnen Achsen des Tensor-Ellipsoids mit ihrem Durchschnitt verglichen werden. Wenn es einen großen Unterschied gibt (wie in der Abbildung oben), dann ist die FA hoch und repräsentiert anisotrope Diffusion. Normale Trakte der weißen Substanz haben eine hohe FA, die bei vielen Krankheitsprozessen verloren geht.

Tractographie. Schließlich kann DTI gute niedrig aufgelöste Bilder von allgemeinen Traktrichtungen der weißen Substanz erzeugen; durch Berechnung der Hauptrichtung des Tensorellipsoids erhalten wir die durchschnittliche Richtung der Axonalbündel im Voxel. Wir können Voxel nach Richtung farbcodieren und erhalten so eine Traktographiekarte. Eine viel anspruchsvollere, hochauflösende Traktographie kann durch Messung der Diffusion in mehr Richtungen erhalten werden. Dabei können Bereiche mit sich kreuzenden Faserbündeln berücksichtigt werden (die bei der normalen DTI einfach herausgemittelt würden). Mit Hilfe dieser Karten können wir 3-dimensioale in vivo Gehirnkonnektivitätskarten erstellen. Dies ist derzeit ein aktives Forschungsgebiet.

Intravoxel Incoherent Motion

Die traditionelle DWI geht davon aus, dass sich alle Wassermoleküle innerhalb eines Voxels gleich verhalten (daher ein einziger ADC pro Voxel). Das stimmt natürlich nicht: Wassermoleküle erleben selbst innerhalb eines einzelnen Voxels sehr unterschiedliche Umgebungen. Moleküle im fließenden Blut haben eine Basisgeschwindigkeit und diffundieren daher sehr schnell; intra- und extrazelluläre Kompartimente haben ebenfalls eine unterschiedliche Diffusivität. Während das vereinfachte Modell für die meisten klinischen Zwecke (z. B. Schlaganfall) ausreichend ist, deuten neue Daten darauf hin, dass einige klinisch relevante Befunde in komplexeren Modellen gefunden werden können. Die beiden Hauptkategorien der fortgeschrittenen Diffusionsmodellierung sind die Diffusionskurtose-Bildgebung, die hier nicht diskutiert wird, und die intravoxel inkohärente Bewegung (IVIM).

In unserer obigen Diskussion über ADC haben wir angenommen, dass die Beziehung zwischen b-Wert und Signalintensität linear ist – mit anderen Worten, dass es einen einzigen ADC-Wert für ein Voxel gibt. Tatsächlich ist die Beziehung in einigen Geweben nicht linear. Insbesondere ist der Signalintensitätsabfall bei niedrigen b-Werten viel steiler; dies impliziert, dass es eine kleine Unterpopulation von sehr schnell diffundierenden Wassermolekülen gibt. Dieses Phänomen ist in der Leber am auffälligsten, und es wird angenommen, dass es mit dem Blutfluss in den Kapillaren zusammenhängt (obwohl unser Verständnis unvollständig ist). Um IVIM zu messen, müssen wir statt derADC -Messung mit 3 b-Werten mehr verwenden (z. B. 8) – insbesondere bei niedrigen b-Werten. Derzeit wird IVIM als Maß für Leberfibrose erforscht.

1. Hagmann P, et al. „Understanding Diffusion MR Imaging Techniques: From Scalar Diffusion-weighted Imaging to Diffusion Tensor Imaging and Beyond.“ Radiographics 26(S1): S205.
2. Koh D, et al. „Intravoxel Incoherent Motion in Body Diffusion-Weighted MRI: Reality and Challenges.“ Am J Roentgenol 188(6): 1622.
3. Dietrich O, et al. „Technical aspects of MR diffusion imaging of the body.“ Eur J Radiol 76: 314.
4. „Chemical Shift: Phase Effects.“ MRI-Questions – Diskussion über die Übertreibung der chemischen Verschiebung in EPI-Sequenzen.
5. Wenn Sie sich für die ursprüngliche (sehr technische!) Arbeit über DWI interessieren: Stejskal EO und Tanner JE. „Spin Diffusion Measurements: Spin Echoes in the Presence of a TimeDependent Field Gradient.“ J Chem Phys 42 (288): 288.