Konzepte in der Statistik

Eigenschaften von r

Wir besprechen und veranschaulichen nun einige wichtige Eigenschaften des Korrelationskoeffizienten als numerisches Maß für die Stärke einer linearen Beziehung.

1. Die Korrelation ändert sich nicht, wenn sich die Maßeinheiten einer der beiden Variablen ändern. Mit anderen Worten, wenn wir die Maßeinheiten der erklärenden Variable und/oder der Antwortvariable ändern, hat dies keine Auswirkung auf die Korrelation (r).

Zur Veranschaulichung vergleichen Sie die beiden Versionen des Streudiagramms der Beziehung zwischen dem Alter eines Fahrers und der maximalen Entfernung zum Lesen eines Autobahnschildes.

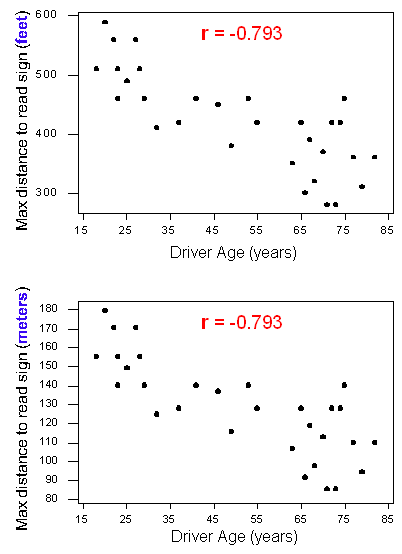
Das obere Streudiagramm zeigt die Originaldaten, bei denen die maximalen Entfernungen in Fuß gemessen werden. Das untere Streudiagramm zeigt die gleiche Beziehung, wobei die maximalen Entfernungen in Meter geändert wurden. Beachten Sie, dass sich die y-Werte geändert haben, die Korrelationen aber gleich geblieben sind. Dieses Beispiel veranschaulicht, dass eine Änderung der Einheiten r nicht ändert. Dies gilt auch dann, wenn wir die Einheiten beider Variablen ändern. Das ist sinnvoll, weil eine Änderung der Einheiten das Muster in den Daten nicht ändert. Die Richtung, Form und Stärke der Beziehung bleiben gleich. Da r Richtung und Stärke einer linearen Beziehung misst, bleibt der Wert von r gleich.

2. Die Korrelation misst nur die Stärke einer linearen Beziehung zwischen zwei Variablen. Sie ignoriert jede andere Art von Beziehung, unabhängig davon, wie stark sie ist. Betrachten Sie zum Beispiel die Beziehung zwischen dem durchschnittlichen Kraftstoffverbrauch beim Fahren einer festgelegten Strecke mit einem Auto und der Geschwindigkeit, mit der das Auto fährt:

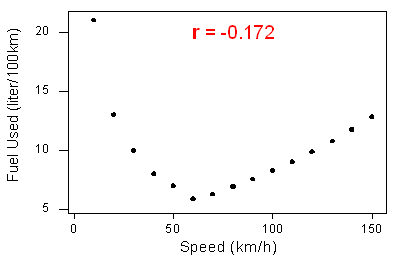
Die Daten haben eine glatte kurvilineare Form. Die Beziehung ist sehr stark, weil die Daten der Kurve perfekt folgen.

Beachten Sie, dass die Korrelation r = -0,172 eine schwache lineare Beziehung anzeigt. Das macht Sinn, weil die Daten nicht genau einer linearen Form folgen. Der Korrelationskoeffizient gibt also nur Auskunft über die Stärke eines linearen Zusammenhangs. Er gibt keine verlässlichen Informationen über die Stärke einer krummlinigen Beziehung.

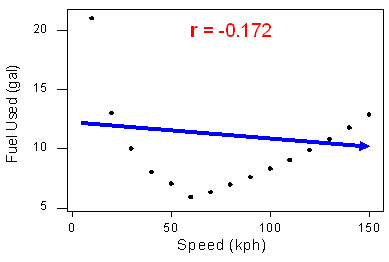
Dieses Beispiel illustriert, dass der Korrelationskoeffizient als Maß für die Stärke nutzlos ist, wenn die Beziehung nicht linear ist. Es veranschaulicht auch eine wichtige Regel: Machen Sie immer einen Scatterplot der Daten, bevor Sie die Bedeutung von r berechnen und interpretieren.

Warum sollten wir zuerst einen Scatterplot machen? Welchen Fehler könnten wir machen, wenn wir uns das Streudiagramm nicht ansehen, sondern nur r betrachten? Wir könnten den Schluss ziehen, dass die Beziehung zwischen den Variablen schwach ist (oder dass es keine Beziehung gibt), weil r nahe bei Null liegt. Aber diese Schlussfolgerung ist falsch. Wir haben „r nahe bei 0“ als Indikator für eine schwache Beziehung oder keine Beziehung und nicht für eine schwache lineare Beziehung oder keine lineare Beziehung fehlinterpretiert. Wir können diese Fehlinterpretation von r leicht vermeiden, indem wir uns das Streudiagramm ansehen.

Fassen wir zusammen. Wenn r nahe bei Null liegt, bedeutet das, dass die Daten eine sehr schwache lineare Beziehung oder keine lineare Beziehung haben. Wenn r nahe bei Null liegt, ist es möglich, dass die Daten eine starke kurvilineare Beziehung haben (wie wir in diesem Beispiel gesehen haben). Um Fehler zu vermeiden, müssen wir uns die Form der Daten im Streudiagramm ansehen, bevor wir r berechnen und interpretieren. Wenn die Form nicht linear ist, sollten Sie r nicht verwenden.

3. Die Korrelation allein reicht nicht aus, um zu bestimmen, ob eine Beziehung linear ist. Um dies zu sehen, lassen Sie uns eine Situation mit einem r-Wert betrachten, der nahe bei 1 liegt, aber eine Beziehung, die nicht linear ist. Erinnern Sie sich an die Studie, in der die Teilnehmer für das Ausfüllen einer Umfrage bezahlt wurden. Die Studie untersuchte die Beziehung zwischen der Höhe des monetären Anreizes und dem Prozentsatz der Stichprobe, der die Umfrage zurücksandte.

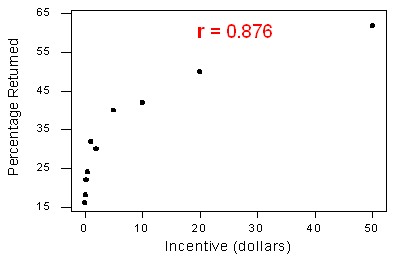
Die Variablen haben eine starke kurvenförmige Beziehung, dennoch ist die Korrelation r = 0.876, also ziemlich nahe bei 1.

Bei Betrachtung der letzten beiden Beispiele sehen wir, dass starke krummlinige Beziehungen eine Korrelation nahe bei 0 oder nahe bei 1 haben können. Die Korrelation allein sagt uns also nicht, ob eine Beziehung linear ist. Wir müssen uns ein Streudiagramm der Daten ansehen.

Schauen Sie sich immer die Daten an!

4. Die Korrelation wird durch Ausreißer stark beeinflusst. Wie Sie in den nächsten beiden Aktivitäten lernen werden, hängt die Art und Weise, wie der Ausreißer die Korrelation beeinflusst, davon ab, ob der Ausreißer mit dem Muster der linearen Beziehung übereinstimmt oder nicht.

Anhand der folgenden Simulation wollen wir untersuchen, wie ein Ausreißer die Korrelation beeinflusst.

Klicken Sie hier, um diese Simulation in einem eigenen Fenster zu öffnen.

Um zu sehen, wie sich ein Ausreißer auf die Korrelation auswirkt, gehen Sie wie folgt vor:

1. Füllen Sie das Streudiagramm mit einer hypothetischen positiven linearen Beziehung zwischen X und Y (indem Sie etwa ein Dutzend Mal auf das Diagramm klicken, beginnend unten links und diagonal nach oben rechts). Achten Sie auf den Korrelationskoeffizienten, der links oben berechnet wird. (Wenn Sie auf den Mülleimer klicken, können Sie von vorne beginnen.)
2. Wenn Sie mit Ihren hypothetischen Daten zufrieden sind, erstellen Sie einen Ausreißer, indem Sie auf einen der Datenpunkte oben rechts im Diagramm klicken und ihn an der rechten Seite des Diagramms nach unten ziehen. Achten Sie wieder darauf, was mit dem Wert der Korrelation passiert.

Was hat diese Übung gezeigt? Diese Aktivität veranschaulicht, dass die Korrelation abnimmt, wenn der Ausreißer vom Muster der Beziehung abweicht. Indem Sie einen Datenpunkt von rechts oben nach rechts unten gezogen haben, haben Sie einen Ausreißer erzeugt, der nicht zu der positiven Assoziation im Rest der Daten passt. Dies verringert die Stärke der linearen Beziehung und verursacht eine Abnahme von r .

In der nächsten Aktivität werden Sie sehen, wie die Korrelation zunimmt, wenn der Ausreißer mit der Richtung der linearen Beziehung übereinstimmt.

Let’s Summarize

• Ein Spezialfall der Beziehung zwischen zwei quantitativen Variablen ist die lineare Beziehung, bei der eine gerade Linie die Beziehung einfach und adäquat zusammenfasst.
• Wenn das Streudiagramm eine lineare Beziehung anzeigt, ergänzen wir es durch den Korrelationskoeffizienten (r), der die Stärke und Richtung einer linearen Beziehung zwischen zwei quantitativen Variablen misst. Der Korrelationskoeffizient liegt zwischen -1 und 1. Werte in der Nähe von -1 zeigen eine starke negative lineare Beziehung an, Werte in der Nähe von 0 zeigen eine schwache lineare Beziehung an und Werte in der Nähe von 1 zeigen eine starke positive lineare Beziehung an.
• Die Korrelation ist ein geeignetes numerisches Maß nur für lineare Beziehungen und ist empfindlich gegenüber Ausreißern. Daher sollte die Korrelation nur als Ergänzung zu einem Streudiagramm verwendet werden (nachdem wir uns die Daten angesehen haben).