Die Ursprünge der Geometrie
Die ersten Linien, die sich die Menschen ausdachten, waren Geraden und Kreise. Sie waren die Geburtsstunde der Geometrie, was wörtlich übersetzt „Vermessung der Erde“ bedeutet und uns eine genaue Vorstellung davon gibt, wofür diese Linien gedacht waren. Die ersten Geometrieexperten waren Landvermesser im alten Ägypten. Die Griechen nannten sie „Arpedonapti“ – diejenigen, die Seile knoten. Die ägyptischen Experten zogen Seile auf dem Land an, um Linien und Kreise zu markieren. Spuren dieser antiken Verwendung sind noch in vielen modernen Sprachen zu finden, wie z. B. in der Redewendung „eine Linie ziehen“. Der Einsatz von Seilen für Vermessungsarbeiten ist über mehrere Jahrhunderte unverändert geblieben und findet sich auch in jüngerer Zeit noch in der Arbeit von Landvermessern.
Griechische Historiker bezeugen die Geburt der Geometrie (wörtlich: Erdvermessung) in Ägypten. Herodot sagt:
Wenn der Fluss einfach die Grenzen des Grundstücks aufgehoben hatte, war es die Aufgabe der Beamten, die genauen Einteilungen neu zu zeichnen.
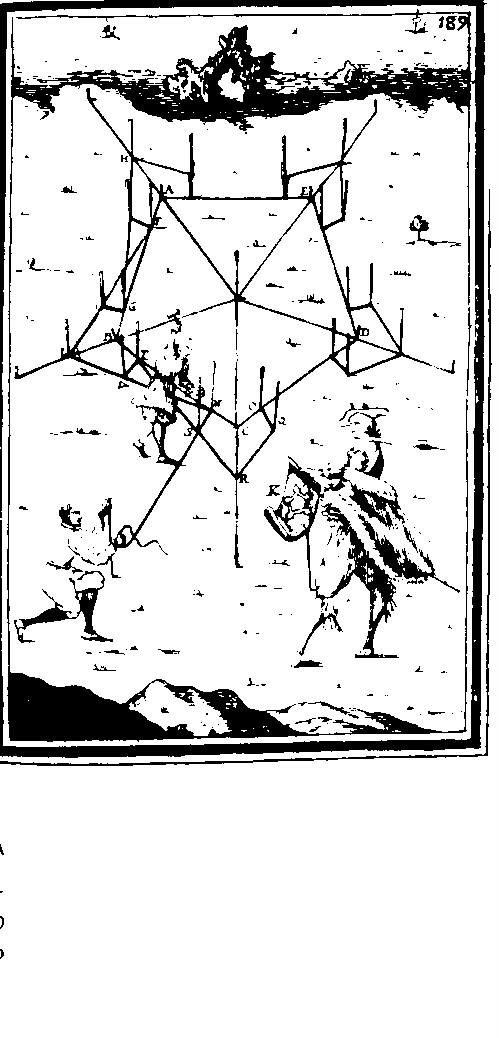 Ägyptische Geometrieexperten wurden „arpedonapti“ genannt, diejenigen, die Seile knoten. Durch das Spannen von Seilen zeichneten sie die beiden einfachsten und wichtigsten Linien in der Geometrie: die Gerade und den Kreis. Die erste, indem sie einfach ein Seil zwischen zwei Punkten spannten, eine Art von Operation, deren Bild noch immer in den Ausdrücken „eine Linie ziehen“, „ein Lot ziehen“ präsent ist; die zweite, indem sie einen der beiden Punkte um den anderen, der fest gehalten wird, drehen ließen. Konnten sie sich das Ausmaß der Entwicklung dieser beiden elementaren Praktiken vorstellen? Wahrscheinlich nicht. In der Tat dürften die praktischen Bedürfnisse der antiken Landvermesser bald die Notwendigkeit von Arbeiten der Art hervorgerufen haben, die wir heute „mit Winkel und Zirkel“ nennen und die eigentlich „mit Kreisen und Geraden“ heißen müssten.
Ägyptische Geometrieexperten wurden „arpedonapti“ genannt, diejenigen, die Seile knoten. Durch das Spannen von Seilen zeichneten sie die beiden einfachsten und wichtigsten Linien in der Geometrie: die Gerade und den Kreis. Die erste, indem sie einfach ein Seil zwischen zwei Punkten spannten, eine Art von Operation, deren Bild noch immer in den Ausdrücken „eine Linie ziehen“, „ein Lot ziehen“ präsent ist; die zweite, indem sie einen der beiden Punkte um den anderen, der fest gehalten wird, drehen ließen. Konnten sie sich das Ausmaß der Entwicklung dieser beiden elementaren Praktiken vorstellen? Wahrscheinlich nicht. In der Tat dürften die praktischen Bedürfnisse der antiken Landvermesser bald die Notwendigkeit von Arbeiten der Art hervorgerufen haben, die wir heute „mit Winkel und Zirkel“ nennen und die eigentlich „mit Kreisen und Geraden“ heißen müssten.
Heute ist es so selbstverständlich, Papier als den natürlichen Schauplatz der Geometrie zu betrachten, dass wir den Gebrauch von Winkel und Zirkel allein als eine willkürliche Beschränkung ansehen, die von spekulativen Geistern eingeführt wurde, die eine geringe Anzahl von Axiomen den vielfältigen Annehmlichkeiten vorzogen, die sich aus der Vielzahl der Instrumente ergeben. Der Unterschied zwischen dem theoretischen Geometrieexperten – ich beziehe mich natürlich auf den klassischen, euklidischen – und dem Techniker – demjenigen, der Maß nimmt, dem Architekten – besteht also hauptsächlich darin, dass der erste freiwillig auf Instrumente, Winkel und Stromabnehmer verzichtet, die der zweite zu seinem Vorteil nutzt.
Auf diese Weise neigen wir dazu, die Geometrie „auf dem Feld“ zugunsten derjenigen „auf dem Papier“ völlig zu ignorieren, wobei wir nicht erkennen, dass die Übertragung geometrischer Operationen vom Feld auf das Papier manchmal völlig andere Techniken und Methoden erfordert.
Man sollte nicht übersehen, dass die Präzision eines Plans im Feld (für denjenigen, der ein Stück Land ausmisst und in Teile unterteilt, wie auch für den Architekten, der ein Gebäude baut – meistens sind diese beiden ein und dieselbe Person -) viel notwendiger ist als auf dem Papier.
Der Architekt, der eine klare Vorstellung vom Gesamtplan hat und sich an den Prozess erinnert, dem er gefolgt ist, um ihn zu erstellen, würde einen Entwurf benötigen. Relativ neue wie auch alte Karten, die zwangsläufig mit rudimentären Instrumenten und Hilfsmitteln gezeichnet wurden, geben die Grenzen eines Grundstücks nicht exakt wieder. In der Tat ist dies unmöglich, denn selbst ein Fehler von einem Prozentpunkt – das Mindeste, was in einem einigermaßen großen Maßstab vorkommen könnte – würde zu einem absoluten Fehler führen, der in der Praxis kaum akzeptiert werden könnte. In diesem Fall ist die Kenntnis der Form und der Maße des zu beschreibenden Objekts (ein Feld, ein Gebäude) von grundlegender Bedeutung; es ist dann die Aufgabe des Geometrieexperten, die auf dem Papier fehlende Präzision auf dem Feld zu reproduzieren. Das Gleiche geschieht mit dem Mathematiker, dem die Genauigkeit der Zahlen bei Demonstrationen überhaupt nicht nützlich ist. Die Geometrie auf dem Papier ersetzt die Präzision der Operationen auf dem Feld, durch die Geometrie des mentalen Prozesses.
Im Gegenteil, von der logischen zur materiellen Exaktheit, als Folge der notwendigen Vergrößerung des Maßstabs, um vom Plan zur tatsächlichen Herstellung desselben überzugehen, ist die Handlung des Spannens eines Seils eine der Hauptoperationen geblieben, bis ins alte Ägypten und das alte Griechenland. Diese Praxis hat sich bis in die Neuzeit erhalten, nur durch die Erfindung und Verbesserung bestimmter optischer Instrumente überholt. Während es auf dem Papier recht einfach ist, ein Lot mit Hilfe von Lineal und Winkel zu zeichnen, erfordert die gleiche Operation auf dem Feld, mit dem gleichen Grad an Präzision, radikal andere Methoden. Auf dem Feld ist das Quadrat unbrauchbar, weil es im Verhältnis zu den Abmessungen der Formen zu klein ist. Selbst wenn das Quadrat extrem genau ist, reicht das Lot, das es ziehen kann, höchstens bis zu einem Meter. Wenn wir ein Quadrat von 30 Metern pro Seite markieren müssen, müssen wir diese Linie 30 Mal verlängern. Das wäre eine so ungenaue Operation, dass sie wahrscheinlich zu den gleichen Ergebnissen führen würde, als wenn wir den rechten Winkel grob messen würden.
 Diese Überlegungen bringen uns zurück zur Ausgangsfrage: Welche Techniken wurden von den ägyptischen Vermessern verwendet, um ein quadratisches Stück Land zu zeichnen? Wie haben sie einen quadratischen Winkel erhalten?
Diese Überlegungen bringen uns zurück zur Ausgangsfrage: Welche Techniken wurden von den ägyptischen Vermessern verwendet, um ein quadratisches Stück Land zu zeichnen? Wie haben sie einen quadratischen Winkel erhalten?
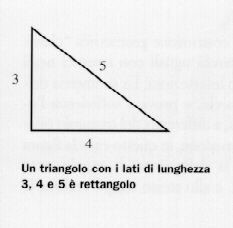
Wie einige Gelehrte vorgeschlagen haben, ist es möglich, dass sie den Satz des Pythagoras (VI. Jahrhundert v. Chr.) kannten oder, genauer gesagt, sich seines Gegenteils bewusst waren, d. h. der Tatsache, dass ein Dreieck mit den Seitenmaßen 3, 4 und 5, bei dem das Quadrat auf der längeren Seite gleich der Summe der Quadrate auf den anderen beiden Seiten ist, ein rechtwinkliges Dreieck ist. Wenn wir also ein Ringseil mit einer Länge von 12 Einheiten, das an drei Punkten im Abstand von 3, 4 und 5 markiert ist, zur Form eines Dreiecks spannen, dessen Scheitelpunkt in den markierten Punkten liegt, ist der Winkel zwischen den kürzesten Seiten des Dreiecks ein rechter Winkel.
Es ist nicht bekannt, ob dies das Verfahren war, das die alten Landvermesser zu ihrer Zeit verwendeten, da nicht bewiesen ist, dass die alten Ägypter wussten, dass das Dreieck mit den Seiten 3, 4 und 5 ein rechtwinkliges Dreieck ist. Selbst wenn sie sich dessen oder anderer pythagoräischer Dreiecke bewusst waren (was durch das Vorhandensein mehrerer pythagoräischer Trios, wenn nicht in der ägyptischen, so doch in der babylonischen Mathematik, stark nahegelegt wird), impliziert dies notwendigerweise, dass sie die Natur des rechten Winkels kannten oder zumindest wussten, wie man ihn herstellt.
Woher kam diesesWissen? Aufgrund des Mangels an auch nur teilweiser Dokumentation und Zeugen können wir versuchen, uns dem Problem von einem anderen Standpunkt aus zu nähern, einem mathematischen und nicht einem historischen. Die Frage, die wir uns stellen müssen, lautet: Was unterscheidet einen rechten Winkel von den anderen? Oder besser: Was ist die Besonderheit des Winkels des Dreiecks mit den Seiten 3, 4 und 5?
Die unmittelbare Antwort lautet: Im Gegensatz zu anderen Dreiecken können pythagoräische Dreiecke und insbesondere das einfachste von ihnen, das mit den Seiten 3, 4 und 5, dazu gebracht werden, sie auf einer Seite zu drehen und dann wieder auf der anderen. Auf diese Weise erhält man eine symmetrische Konfiguration, die den verfügbaren Raum vollständig ausfüllt, ohne Überlappungen oder Lücken.
 Kein anderer Winkel als der rechte hat diese symmetrische Eigenschaft, die im ersten vollständigen Buch der Geometrie, das unsere Zeit erreicht hat, Euklids Elemente (IV. Jahrhundert v. Chr.), eine eigene Definition erhält:
Kein anderer Winkel als der rechte hat diese symmetrische Eigenschaft, die im ersten vollständigen Buch der Geometrie, das unsere Zeit erreicht hat, Euklids Elemente (IV. Jahrhundert v. Chr.), eine eigene Definition erhält:
Wenn eine gerade Linie, die auf eine andere fällt, gleiche Winkel bildet, so sind diese beiden rechtwinklig.
Das Wesen des rechten Winkels liegt darin, dass die Winkel, die sich aus dem Schnittpunkt zweier Geraden ergeben, gleich sind. Dies lässt sich sofort auf dem Papier demonstrieren, indem man das Papier entlang einer der konvergierenden Linien faltet und überprüft, dass die andere Linie auf sich selbst faltet.
Die „klassische“ geometrische Konstruktion, die darin besteht, zwei Kreise zu markieren und dann ihre Schnittpunkte zu vereinigen, besitzt ebenfalls diese Eigenschaft.
Der symmetrische Charakter der Form ist ganz offensichtlich, und es ist ein klarer Beweis für die Gleichheit der Winkel. Außerdem legt die Form im Gegensatz zum Pythagoradreieck, das einer weiteren Konstruktion bedarf, in diesem Fall durch die Gleichheit der Winkel sofort die Definition des rechten Winkels nahe und konstruiert sich gleichzeitig selbst.
Das sind noch einfache Vermutungen. Zweifellos ist dieser Prozess deutlich einfacher und präziser als der erste. Man könnte sagen, dass wir auf diese Weise nur die Senkrechte markieren, die durch den Mittelpunkt des gegebenen Segments verläuft, auch Achse dieses Segments genannt. Dennoch ist es nicht schwer zu bemerken, dass, wenn wir ein Lot an einem Ende benötigen, wie im Fall des Zeichnens eines Quadrats, es notwendig sein wird, das Segment zu verdoppeln und es in Richtung der Stelle zu verlängern, an der wir das Lot zeichnen wollen, und dann den vorhergehenden Prozess zu wiederholen.
Es ist notwendig zu beachten, dass alle diese Techniken besonders für flaches Land wie die ägyptische Ebene geeignet sind.