Die Reihenfolge der Operationen: PEMDAS

Es scheint, als ob die Antwort davon abhängt, wie man das Problem betrachtet. Aber diese Art von Flexibilität können wir in der Mathematik nicht haben; Mathematik funktioniert nicht, wenn man sich der Antwort nicht sicher sein kann, oder wenn der exakt gleiche Ausdruck so berechnet werden kann, dass man zu zwei oder mehr verschiedenen Antworten kommt.

Um diese Verwirrung zu beseitigen, haben wir einige Vorrangregeln, die mindestens bis ins Jahr 1500 zurückreichen, die sogenannte „Reihenfolge der Operationen“. Die „Operationen“ sind Addition, Subtraktion, Multiplikation, Division, Potenzierung und Gruppierung; die „Reihenfolge“ dieser Operationen gibt an, welche Operationen vor welchen anderen Operationen Vorrang haben (erledigt werden).

Eine gängige Technik, um sich die Reihenfolge der Operationen zu merken, ist die Abkürzung (oder, richtiger, das „Akronym“) „PEMDAS“, die in die mnemonische Phrase „Please Excuse My Dear Aunt Sally“ umgewandelt wird. Diese Phrase steht für „Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction“ und hilft, sich die Reihenfolge zu merken. Diese Auflistung verrät Ihnen die Rangfolge der Operationen: Klammern sind ranghöher als Exponenten, diese ranghöher als Multiplikation und Division (aber Multiplikation und Division stehen auf dem gleichen Rang), und Multiplikation und Division sind ranghöher als Addition und Subtraktion (die zusammen auf dem letzten Rang stehen). Mit anderen Worten, die Rangfolge ist:

Wenn Sie eine Reihe von Operationen gleichen Ranges haben, operieren Sie einfach von links nach rechts. Zum Beispiel ist 15 ÷ 3 × 4 nicht 15 ÷ (3 × 4) = 15 ÷ 12, sondern (15 ÷ 3) × 4 = 5 × 4, weil man von links nach rechts zuerst zum Divisionszeichen kommt.

Wenn Sie sich nicht sicher sind, testen Sie es in Ihrem Taschenrechner, der mit der Reihenfolge der Operationen programmiert wurde. Wenn Sie zum Beispiel den obigen Ausdruck in einen grafischen Taschenrechner eingeben, erhalten Sie:

Anhand der obigen Hierarchie sehen wir, dass bei der Frage „4 + 2×3“ am Anfang dieses Artikels Wahl 2 die richtige Antwort war, weil wir vor der Addition die Multiplikation durchführen müssen.

(Hinweis: Sprecher des britischen Englisch verwenden stattdessen oft das Akronym „BODMAS“, anstatt „PEMDAS“. BODMAS steht für „Brackets, Orders, Division and Multiplication, and Addition and Subtraction“. Da „Klammern“ dasselbe sind wie Klammern und „Ordnungen“ dasselbe sind wie Exponenten, bedeuten die beiden Akronyme dasselbe. Außerdem können Sie sehen, dass das „M“ und das „D“ in der britisch-englischen Version vertauscht sind; dies bestätigt, dass Multiplikation und Division auf demselben „Rang“ oder „Niveau“ stehen. Kanadische Englischsprachige teilen den Unterschied auf, indem sie BEDMAS verwenden.)

Die Reihenfolge der Operationen wurde festgelegt, um Missverständnisse zu vermeiden, aber PEMDAS kann seine eigene Verwirrung erzeugen; einige Schüler neigen manchmal dazu, die Hierarchie so anzuwenden, als ob alle Operationen in einem Problem auf der gleichen „Ebene“ sind (einfach von links nach rechts gehen), aber oft sind diese Operationen nicht „gleich“. Oft hilft es, Probleme von innen nach außen zu bearbeiten, anstatt von links nach rechts, weil oft einige Teile des Problems „tiefer liegen“ als andere Teile. Am besten lässt sich das anhand einiger Beispiele erklären:

• Vereinfachen Sie 4 + 32.

• Vereinfache 4 + (2 + 1)2.

• Vereinfache 4 + 2.

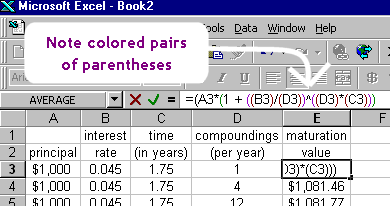
Eine besondere Bedeutung hat die Verwendung von eckigen Klammern (das „“ oben) anstelle von Klammern nicht. Klammern und geschweifte Klammern (die Zeichen „{“ und „}“) werden bei verschachtelten Klammern verwendet, um die Übersicht zu behalten, welche Klammer zu welcher gehört. Die verschiedenen Gruppierungszeichen werden nur der Einfachheit halber verwendet. Dies ist vergleichbar mit dem, was in einer Excel-Tabelle passiert, wenn Sie eine Formel mit Klammern eingeben: Jeder Satz von Klammern ist farblich gekennzeichnet, so dass Sie die Paare erkennen können:

• Vereinfachen

Auf der nächsten Seite finden Sie weitere Arbeitsbeispiele….