17.2 Kombinierte Konduktion und Konvektion

Weiter: 17.3 Dimensionslose Zahlen und Up: 17. Konvektive Wärmeübertragung Previous: 17.1 Die Reynolds-Analogie Contents Index

Wir können nun Probleme analysieren, bei denen sowohl Leitung als auch Konvektion auftreten, und zwar ausgehend von einer Wand, die auf beiden Seiten durch ein strömendes Fluid gekühlt wird. Wie besprochen, kann eine Beschreibung der konvektiven Wärmeübertragung explizit als

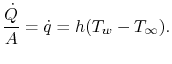
$\displaystyle \frac{\dot{Q}}{A}=\dot{q} = h(T_w-T_\infty).$

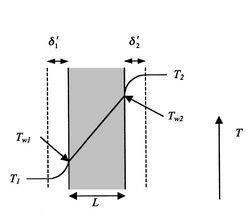
Dies könnte ein Modell einer Turbinenschaufel mit Innenkühlung darstellen. Abbildung 17.6 zeigt die Konfiguration.

Abbildung 17.6:Leitende Wand mit konvektiverWärmeübertragung

Der Wärmeübergang in Fluid 1 ist gegeben durch

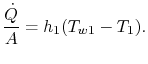
$\displaystyle \frac{\dot{Q}}{A} = h_1(T_{w1}-T_1).$

, was der Wärmeübertragung pro Flächeneinheit auf das Fluid entspricht. Der Wärmeübergang im Fluid 2 ist in ähnlicher Weise gegeben durch

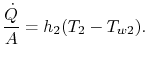
$\displaystyle \frac{\dot{Q}}{A} = h_2 (T_2 -T_{w2}).$

Auf der anderen Seite der Wand haben wir

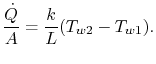
$\displaystyle \frac{\dot{Q}}{A} = \frac{k}{L}(T_{w2} -T_{w1}).$

Die Größe $\dot{Q}/A$ ist in all diesen Ausdrücken gleich.Setzt man sie alle zusammen, um den bekannten Gesamttemperaturabfall zu schreiben, ergibt sich eine Beziehung zwischen Wärmeübertragung und Gesamttemperaturabfall,:

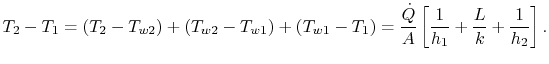$\displaystyle T_2-T_1 = (T_2-T_{w2})+(T_{w2}-T_{w1})+(T_{w1}-T_1) =\frac{\dot{Q}}{A}\left.$

(17..20)

Wir können einen thermischen Widerstand,, definieren, wie zuvor, so dass

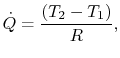
$\displaystyle \dot{Q} =\frac{(T_2 -T_1)}{R},$

wobeigegeben ist durch

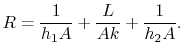$\displaystyle R = \frac{1}{h_1A} + \frac{L}{Ak} + \frac{1}{h_2A}.$

(17..21)

Gleichung (17.21) ist der Wärmewiderstand für eine feste Wand mit Konvektionswärmeübertragung auf jeder Seite.

Für eine Turbinenschaufel in einem Gasturbinentriebwerk ist die Kühlung eine kritische Überlegung. In Bezug auf Abbildung 17.6 ist die Temperatur am Brennkammeraustritt (Turbineneintritt) und die Temperatur am Verdichterausgang. Wir wollen $T_{w2}$ finden, weil dies die höchste Metalltemperatur ist. Aus(17.20), kann die Wandtemperatur geschrieben werden als

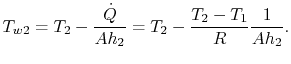$\displaystyle T_{w2} = T_2 - \frac{\dot{Q}}{Ah_2}= T_2 - \frac{T_2 - T_1}{R}\frac{1}{Ah_2}.$

(17..22)

Unter Verwendung des Ausdrucks für den thermischen Widerstand, können die Wandtemperaturen in Form von Wärmeübergangskoeffizienten und Wandeigenschaften ausgedrückt werden als

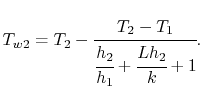$\displaystyle T_{w2} = T_2 - \cfrac{T_2 - T_1}{\cfrac{h_2}{h_1}+\cfrac{Lh_2}{k}+1}.$

(17..23)

Gleichung (17.23) liefert einige grundlegende Designrichtlinien. Das Ziel ist es, einen niedrigen Wert von $T_{w2}$ zu haben. Das bedeutet,sollte groß sein,sollte groß sein (aber wir haben möglicherweise nicht viel Flexibilität bei der Wahl des Materials) undsollte klein sein. Eine Möglichkeit, das erste Ziel zu erreichen, besteht darin,niedrig zu halten (z. B. Kühlluft wie in Abbildung 17.1 ausströmen zu lassen, um die Oberfläche abzuschirmen).

Ein zweites Beispiel für kombinierte Leitung und Konvektion ist ein Zylinder, der einer strömenden Flüssigkeit ausgesetzt ist. Die Geometrie ist inAbbildung 17.7 dargestellt.

Abbildung 17.7:Zylinder in einem strömenden Fluid

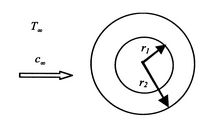
Für den Zylinder ist der Wärmestrom an der Außenfläche gegeben durch

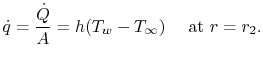
$\displaystyle \dot{q} = \frac{\dot{Q}}{A} = h(T_w-T_infty)\quad \textrm{ at}r=r_2.$

Die Randbedingung an der inneren Oberfläche kann entweder eine Wärmestrombedingung oder eine Temperaturvorgabe sein; wir verwenden letztere zur Vereinfachung der Algebra. Also,bei. Dies ist ein Modell für den Wärmeübergang in einem Rohr mit Radius, das von einer Isolierung der Dickeumgeben ist. Die Lösung für einen zylindrischen Bereich wurde inAbschnitt 16.5.1 als

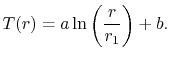
$\displaystyle T(r) =a\ln\left(\frac{r}{r_1}\right) +b gegeben.$

Die Verwendung der Randbedingungergibt.

An der Grenzfläche zwischen dem Zylinder und dem Fluid, , sind die Temperatur und der Wärmestrom stetig. (Frage: Warum ist das so und wie würden Sie das begründen?)

$\displaystyle \dot{q} = \underbrace{-k\frac{dT}{dr}}_{\substack{\textrm{heat fl......2}{r_1}\right)+T_1\right)-T_\infty\right]} _\textrm{Oberflächenwärmestrom zum Fluid}$

(17..24)

Setzt man die Form der Temperaturverteilung im Zylinder in Gleichung (17.24) yields

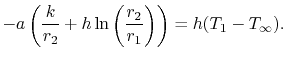
$\displaystyle -a\left(\frac{k}{r_2}+h\ln\left(\frac{r_2}{r_1}\right)\right)=h(T_1-T_\infty).$

Die Integrationskonstante,, ist

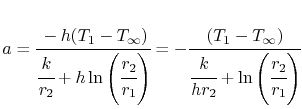
$\displaystyle a=\cfrac{-h(T_1-T_\infty)}{\cfrac{k}{r_2}+h\ln\left(\cfrac{r_2}{r......t)}=-\cfrac{(T_1-T_\infty)}{\cfrac{k}{hr_2}+\ln\left(\cfrac{r_2}{r_1}\right)}$

und der Ausdruck für die Temperatur ist, in normierter, nichtdimensionaler Form,

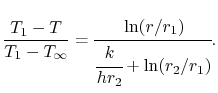$\displaystyle \frac{T_1-T}{T_1-T_\infty} = \cfrac{\ln(r/r_1)}{\cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..25)

Der Wärmefluss pro Längeneinheit, $\dot{Q}$ , ist gegeben durch

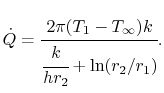$\displaystyle \dot{Q}=\cfrac{2\pi(T_1-T_\infty)k}{\cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..26)

Die Einheiten in Gleichung (17.26) sind W/m-s.

Ein interessantes Problem ist die Wahl der Dämmungsdicke zur Minimierung des Wärmeverlustes für eine feste Temperaturdifferenz $T_1-T_\infty$ zwischen der Rohrinnenseite und der vom Rohr entfernten strömenden Flüssigkeit. ( $T_1-T_\infty$ ist die treibende Temperaturverteilung für das Rohr.) Um das Verhalten des Wärmeübergangs zu verstehen, untersuchen wir den Nenner inGleichung (17.26), wenn variiert. Die Dicke der Isolierung, die eine maximale Wärmeübertragung ergibt, ist gegeben durch

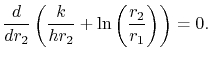$\displaystyle \frac{d}{dr_2}\left(\frac{k}{hr_2}+\ln\left(\frac{r_2}{r_1}\right)\right)=0.$

(17..27)

(Frage: Woher wissen wir, dass dies ein Maximum ist?)

Aus Gleichung (17.27), ist der Wert von für das Maximum $\dot{Q}$ also

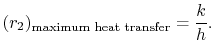$\displaystyle (r_2)_{\textrm{maximale Wärmeübertragung}} = \frac{k}{h}.$

(17..28)

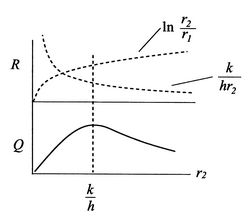
Wennkleiner als dieser Wert ist, können wir eine Isolierung hinzufügen und den Wärmeverlust erhöhen. Um zu verstehen, warum dies geschieht, betrachten Sie Abbildung 17.8, die ein Schema des Wärmewiderstands und der Wärmeübertragung zeigt. Wennvon einem Wert kleiner alsansteigt, treten zwei Effekte auf. Erstens nimmt die Dicke der Isolierung zu, wodurch der Wärmeübergang tendenziell sinkt, weil der Temperaturgradient abnimmt, und zweitens nimmt die Fläche der Außenfläche der Isolierung zu, wodurch der Wärmeübergang tendenziell steigt. Der zweite ist (lose) mit dem-Term verbunden, der erste mit dem $\ln(r_2/r_1)$ -Term. Es gibt also zwei konkurrierende Effekte, die zusammen ein Maximum $\dot{Q}$ beiergeben.