PEMDASE-voorbeeldenEen probleem
Purplemath
Als je gevraagd wordt om iets als “4 + 2×3” te vereenvoudigen, dan is de vraag die natuurlijk opkomt: “Op welke manier doe ik dat? Want er zijn twee mogelijkheden!” Ik zou eerst kunnen optellen:
4 + 2×3 = (4 + 2)×3 = 6×3 = 18
…of ik zou eerst kunnen vermenigvuldigen:
4 + 2×3 = 4 + (2×3) = 4 + 6 = 10
Welk antwoord is het juiste?
Content Continues Below
MathHelp.com

Het lijkt erop dat het antwoord afhangt van de manier waarop je naar het probleem kijkt. Maar in de wiskunde kunnen we dit soort flexibiliteit niet hebben; wiskunde werkt niet als je niet zeker kunt zijn van het antwoord, of als exact dezelfde uitdrukking kan worden berekend zodat je op twee of meer verschillende antwoorden kunt uitkomen.
Affiliate
Om deze verwarring weg te nemen, hebben we een aantal voorrangsregels, minstens al in de jaren 1500 vastgesteld, die de “volgorde van bewerkingen” worden genoemd. De “operaties” zijn optellen, aftrekken, vermenigvuldigen, delen, exponentiëren en groeperen; de “volgorde” van deze operaties geeft aan welke operaties voorrang hebben (worden afgehandeld) vóór welke andere operaties.
Een veelgebruikte techniek om de volgorde van operaties te onthouden is de afkorting (of, beter gezegd, het “acroniem”) “PEMDAS”, die wordt omgezet in de mnemotechnische uitdrukking “Please Excuse My Dear Aunt Sally”. Deze zin staat voor, en helpt bij het onthouden van, de volgorde van “Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction”. Deze opsomming vertelt je de rangorde van de operaties: Haakjes staan hoger dan exponenten, die hoger staan dan vermenigvuldigen en delen (maar vermenigvuldigen en delen staan op dezelfde rang), en vermenigvuldigen en delen staan hoger dan optellen en aftrekken (die samen op de onderste rang staan). Met andere woorden, de rangorde is:
- Parentheses (vereenvoudig binnen ‘em)
- Exponenten
- Vermenigvuldiging en deling (van links naar rechts)
- Toevoeging en Aftrekking (van links naar rechts)
Wanneer je een stel bewerkingen van dezelfde rang hebt, opereer je gewoon van links naar rechts. Zo is 15 ÷ 3 × 4 niet 15 ÷ (3 × 4) = 15 ÷ 12, maar is het eerder (15 ÷ 3) × 4 = 5 × 4, omdat je van links naar rechts eerst bij het deelteken komt.
Als je hier niet zeker van bent, test het dan in je rekenmachine, die is geprogrammeerd met de hiërarchie van de volgorde van bewerkingen. Als je bijvoorbeeld de bovenstaande uitdrukking in een grafische rekenmachine typt, krijg je:

Gebruik makend van bovenstaande hiërarchie, zien we dat, in de “4 + 2×3” vraag aan het begin van dit artikel, keuze 2 het juiste antwoord was, omdat we de vermenigvuldiging moeten doen voordat we de optelling doen.
Content Continues Below
(Opmerking: Sprekers van Brits Engels gebruiken in plaats van “PEMDAS” vaak het acroniem “BODMAS”. BODMAS staat voor “Haakjes, Orders, Delen en Vermenigvuldigen, en Optellen en Aftrekken”. Aangezien “haakjes” hetzelfde zijn als haakjes en “volgordes” hetzelfde zijn als exponenten, betekenen de twee acroniemen hetzelfde. U kunt ook zien dat de “M” en de “D” in de Brits-Engelse versie zijn omgekeerd; dit bevestigt dat vermenigvuldigen en delen op dezelfde “rang” of “niveau” staan. Canadese Engelstaligen splitsen het verschil, met behulp van BEDMAS.)
De volgorde van bewerkingen is vastgesteld om miscommunicatie te voorkomen, maar PEMDAS kan zijn eigen verwarring genereren; sommige leerlingen hebben soms de neiging om de hiërarchie toe te passen alsof alle bewerkingen in een probleem op hetzelfde “niveau” zitten (gewoon van links naar rechts), maar vaak zijn die bewerkingen niet “gelijk”. Vaak helpt het om problemen van binnen naar buiten te werken, in plaats van van links naar rechts, omdat sommige delen van het probleem vaak “dieper” liggen dan andere delen. De beste manier om dit uit te leggen is aan de hand van enkele voorbeelden:
-
Vergelijk 4 + 32.
Ik moet de term met de exponent vereenvoudigen voordat ik de 4 probeer toe te voegen:
4 + 32 = 4 + 9 = 13
-
Vereenvoudig 4 + (2 + 1)2.
Ik moet eerst vereenvoudigen binnen de haakjes voordat ik de exponent kan doorrekenen. Pas dan kan ik de optelling van de 4 doen.
4 + (2 + 1)2 = 4 + (3)2 = 4 + 9 = 13
Versimpeling
-
Versimpelen 4 + 2.
Affiliate
Ik moet niet proberen om deze geneste haakjes van links naar rechts te doen; die methode is gewoon te foutgevoelig. In plaats daarvan zal ik proberen om van binnen naar buiten te werken. Eerst vereenvoudig ik binnen de gekromde haakjes, dan vereenvoudig ik binnen de vierkante haakjes, en dan pas zorg ik voor de kwadratuur. Als dat gedaan is, kan ik eindelijk de 4 toevoegen:
4 + 2
= 4 + 2
= 4 + 2
= 4 + 9
= 13
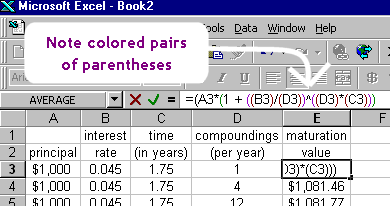
Er is geen bijzondere betekenis in het gebruik van vierkante haakjes (de “” hierboven) in plaats van haakjes. Haakjes en accolades (de “{” en “}” tekens) worden gebruikt wanneer er geneste haakjes zijn, als een hulpmiddel om bij te houden welke haakjes bij welke horen. De verschillende groeperingstekens worden alleen voor het gemak gebruikt. Dit is vergelijkbaar met wat er in een Excel-spreadsheet gebeurt wanneer je een formule met haakjes invoert: elke set haakjes krijgt een kleurcode, zodat je de paren kunt onderscheiden:
-
Vereenvoudigen
Ik zal eerst vereenvoudigen binnen de haakjes:
Dus mijn versimpelde antwoord is
Op de volgende pagina staan meer uitgewerkte voorbeelden….
URL: https://www.purplemath.com/modules/orderops.htm
Pagina 1Pagina 2Pagina 3