Concepten in de statistiek

Eigenschappen van r

We bespreken en illustreren nu verschillende belangrijke eigenschappen van de correlatiecoëfficiënt als numerieke maat voor de sterkte van een lineair verband.

1. De correlatie verandert niet wanneer de meeteenheden van een van de variabelen veranderen. Met andere woorden, als we de meeteenheden van de verklarende variabele en/of de responsvariabele veranderen, heeft dat geen effect op de correlatie (r).

Om dit te illustreren, vergelijk de twee versies van de scatterplot van de relatie tussen de leeftijd van een bestuurder en de maximale afstand voor het lezen van een verkeersbord.

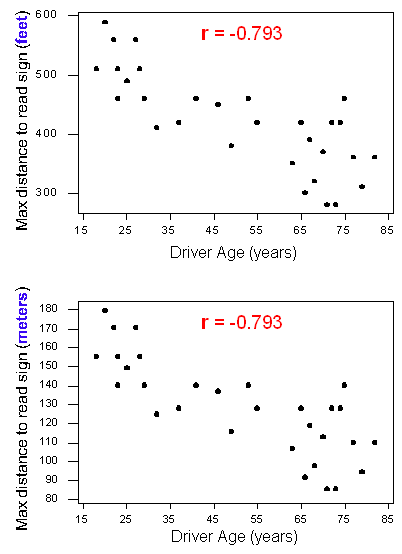
De bovenste scatterplot geeft de oorspronkelijke gegevens weer, waarbij de maximumafstanden in voeten zijn gemeten. De onderste scatterplot toont dezelfde relatie, maar met de maximumafstanden veranderd in meters. Merk op dat de y-waarden zijn veranderd, maar dat de correlaties hetzelfde zijn. Dit voorbeeld illustreert dat een verandering van eenheid niet leidt tot een verandering van r. Dit is waar, zelfs als we de eenheden van beide variabelen veranderen. Dit is logisch omdat een verandering in de eenheden het patroon in de gegevens niet verandert. De richting, de vorm en de sterkte van het verband blijven dezelfde. Aangezien r de richting en de sterkte van een lineair verband meet, blijft de waarde van r gelijk.

2. De correlatie meet alleen de sterkte van een lineair verband tussen twee variabelen. Zij negeert elk ander type verband, hoe sterk dat ook is. Neem bijvoorbeeld het verband tussen het gemiddelde brandstofverbruik bij het rijden van een vaste afstand in een auto en de snelheid waarmee de auto rijdt:

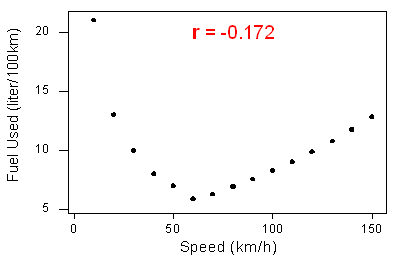
De gegevens hebben een vloeiende kromlijnige vorm. Het verband is zeer sterk omdat de gegevens de kromme perfect volgen.

Merk op dat de correlatie r = -0,172 wijst op een zwak lineair verband. Dit is logisch omdat de gegevens geen lineaire vorm volgen. De correlatiecoëfficiënt geeft dus alleen informatie over de sterkte van een lineair verband. Hij geeft geen betrouwbare informatie over de sterkte van een kromlijnige relatie.

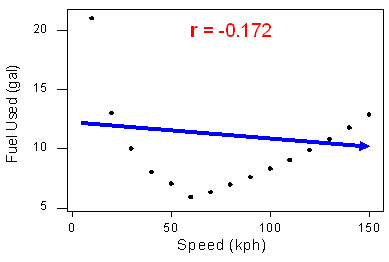
Dit voorbeeld illustreert dat de correlatiecoëfficiënt nutteloos is als maatstaf voor sterkte als de relatie niet lineair is. Het illustreert ook een belangrijke regel: Maak altijd eerst een scatterplot van de gegevens voordat je de betekenis van r berekent en interpreteert.

Waarom moeten we eerst een scatterplot maken? Als we niet naar de scatterplot zouden kijken, maar alleen naar r, welke fout zouden we dan kunnen maken? We zouden kunnen concluderen dat het verband tussen de variabelen zwak is (of dat er geen verband is) omdat r dicht bij nul ligt. Maar deze conclusie is fout. We hebben “r dicht bij 0” verkeerd geïnterpreteerd als een indicator van een zwak verband of geen verband in plaats van een zwak lineair verband of geen lineair verband. We kunnen deze verkeerde interpretatie van r gemakkelijk vermijden door naar de scatterplot te kijken.

Laten we even samenvatten. Als r dicht bij nul ligt, betekent dit dat de gegevens een zeer zwak lineair verband of geen lineair verband hebben. Als r dicht bij nul ligt, is het mogelijk dat de gegevens een sterk kromlijnig verband hebben (zoals we in dit voorbeeld zagen). Om fouten te voorkomen, moeten we naar de vorm van de gegevens in de scatterplot kijken voordat we r berekenen en interpreteren. Als de vorm niet lineair is, gebruik r dan niet.

3. De correlatie op zichzelf is niet genoeg om te bepalen of een relatie lineair is. Laten we, om dit te zien, eens kijken naar een situatie met een r-waarde die dicht bij 1 ligt, maar een relatie die niet lineair is. Denk aan het onderzoek waarbij deelnemers werden betaald om een enquête in te vullen. De studie onderzocht de relatie tussen het bedrag van de geldelijke stimulans en het percentage van de steekproef dat de enquête terugstuurde.

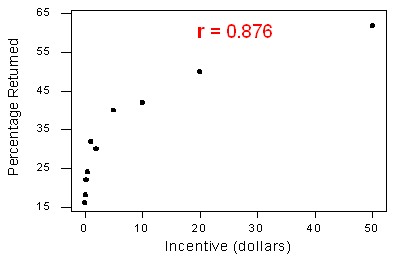
De variabelen hebben een sterk kromlijnig verband, maar de correlatie is r = 0.876, dicht bij 1.

Als we de laatste twee voorbeelden bekijken, zien we dat sterke kromlijnige relaties een correlatie kunnen hebben die dicht bij 0 of dicht bij 1 ligt. Dus de correlatie alleen zegt ons niet of een relatie lineair is. We moeten kijken naar een scatterplot van de gegevens.

Kijk altijd naar de gegevens!

4. De correlatie wordt sterk beïnvloed door uitbijters. Zoals je in de volgende twee activiteiten zult leren, hangt de manier waarop de uitbijter de correlatie beïnvloedt af van de vraag of de uitbijter consistent is met het patroon van het lineaire verband of niet.

Met behulp van de onderstaande simulatie gaan we onderzoeken hoe een uitbijter de correlatie beïnvloedt.

Klik hier om deze simulatie in een eigen venster te openen.

Om te zien hoe een uitschieter de correlatie beïnvloedt, doe je het volgende:

1. Vul de scatterplot met een hypothetisch positief lineair verband tussen X en Y (door ongeveer een dozijn keer op de grafiek te klikken, beginnend linksonder en diagonaal omhoog naar rechtsboven). Let op de correlatiecoëfficiënt die linksboven in de simulatie wordt berekend. (Als je op de vuilnisbak klikt, kun je opnieuw beginnen.)
2. Als je tevreden bent met je hypothetische gegevens, maak je een uitbijter door op een van de gegevenspunten rechtsboven in de grafiek te klikken en deze langs de rechterkant van de grafiek naar beneden te slepen. Let ook nu weer op wat er met de waarde van de correlatie gebeurt.

Wat heeft deze activiteit geïllustreerd? Deze activiteit illustreert dat de correlatie afneemt wanneer de uitbijter afwijkt van het patroon van de relatie. Door een gegevenspunt van rechtsboven naar rechtsonder te slepen, heb je een uitbijter gecreëerd die niet past bij het positieve verband in de rest van de gegevens. Dit vermindert de sterkte van het lineaire verband en veroorzaakt een afname van r .

In de volgende activiteit zul je zien hoe de correlatie toeneemt wanneer de uitbijter in overeenstemming is met de richting van het lineaire verband.

Let’s Summarize

• Een speciaal geval van het verband tussen twee kwantitatieve variabelen is het lineaire verband waarbij een rechte lijn het verband eenvoudig en adequaat samenvat.
• Wanneer de scatterplot een lineair verband weergeeft, vullen we deze aan met de correlatiecoëfficiënt (r), die de sterkte en richting van een lineair verband tussen twee kwantitatieve variabelen meet. De correlatiecoëfficiënt ligt tussen -1 en 1. Waarden in de buurt van -1 wijzen op een sterk negatief lineair verband, waarden in de buurt van 0 wijzen op een zwak lineair verband en waarden in de buurt van 1 wijzen op een sterk positief lineair verband.
• De correlatie is alleen een geschikte numerieke maat voor lineaire verbanden en is gevoelig voor uitbijters. Daarom moet de correlatie alleen worden gebruikt als aanvulling op een scatterplot (nadat we naar de gegevens hebben gekeken).