4.2: Magnetisch Moment en Koppel

Magnetisch dipoolmoment

Hier introduceren we een snelkoppeling voor toekomstige koppelberekeningen. De grootheid (yz) is de oppervlakte van de lus, (A). In toekomstige toepassingen kunnen we de stroom in de lus laten lopen door een enkele draad, die verschillende keren rond de omtrek wordt gewikkeld. De kracht die aan elke kant van de lus wordt uitgeoefend (en dus het koppel) wordt dan vermenigvuldigd met het aantal windingen in de draad, \(N). Het product van N(N), I(I), en A(A) wordt geschreven als één grootheid, waardoor de grootte van het koppel in dit geval de eenvoudige vorm heeft van TTIU = TTIU B.

Als deze lus om zijn as draait, dan krimpt de momentenarm. Bijvoorbeeld, als de bovenkant van de lus naar achteren draait en de onderkant naar voren met 90°, dan zullen de krachten op die segmenten recht van elkaar af staan. Deze krachten werken recht door de as, dus het koppel dat ze veroorzaken is nul. We weten dat koppel en magnetisch veld beide vectoren zijn, en het gecreëerde koppel is gerelateerd aan de oriëntatie van de lus in het veld. We kunnen de oriëntatie van de lus verklaren door een magnetisch dipoolmoment te definiëren:

De vector (\Overrechtarrow A\) heeft een grootte gelijk aan de oppervlakte van de lus, en heeft een richting die loodrecht staat op het vlak van de lus, in de richting die als volgt gedefinieerd is: Krul de vingers van je rechterhand in een richting die de richting van de stroom rond de lus volgt, en de duim van die hand wijst de richting van de vector aan. Zo zou de lus in figuur 4.2.1 een magnetisch moment hebben dat naar buiten wijst.

De koppelvector kan nu uit het magnetisch dipoolmoment worden berekend op dezelfde manier als het koppel dat op een elektrische dipool wordt uitgeoefend:

We zien dat dit werkt voor het geval in figuur 4.2.1: De hoek tussen het magnetische dipoolmoment (dat buiten de bladzijde wijst) en het magnetische veld is 90o, dus de sinus van de hoek tussen deze vectoren die in het kruisproduct voorkomt is 1, wat het antwoord geeft dat we hierboven vonden. Als de lus om de horizontale as draait, verandert de hoek tussen het magnetisch dipoolmoment en het veld, waardoor de momentarmen van de krachten met een factor ⅓(⅓sin ⅓ta) afnemen – precies de hoeveelheid die in het kruisproduct is opgenomen. Als de lus draait tot het punt waar het vlak loodrecht op het veld staat, zijn het magnetisch moment en het veld evenwijdig, waardoor het koppel nul wordt, zoals we hierboven vonden.

Hoewel we de formule voor het magnetisch dipoolmoment afleidden met een rechthoek, blijkt dat zolang de lus in een vlak ligt, de formule werkt ongeacht welke vorm hij heeft. Als illustratief voorbeeld zullen we het koppel op een cirkelvormige lus oplossen. Dit is een moeilijker voorbeeld dan de rechthoek, om redenen die duidelijk zullen worden, maar het toont wel belangrijke hulpmiddelen voor het integreren van infinitesimale bijdragen en het omgaan met vectorproducten.

Figuur 4.2.2a – Koppel op een gesloten cirkelvormige lus van draad in een eenvormig magnetisch veld

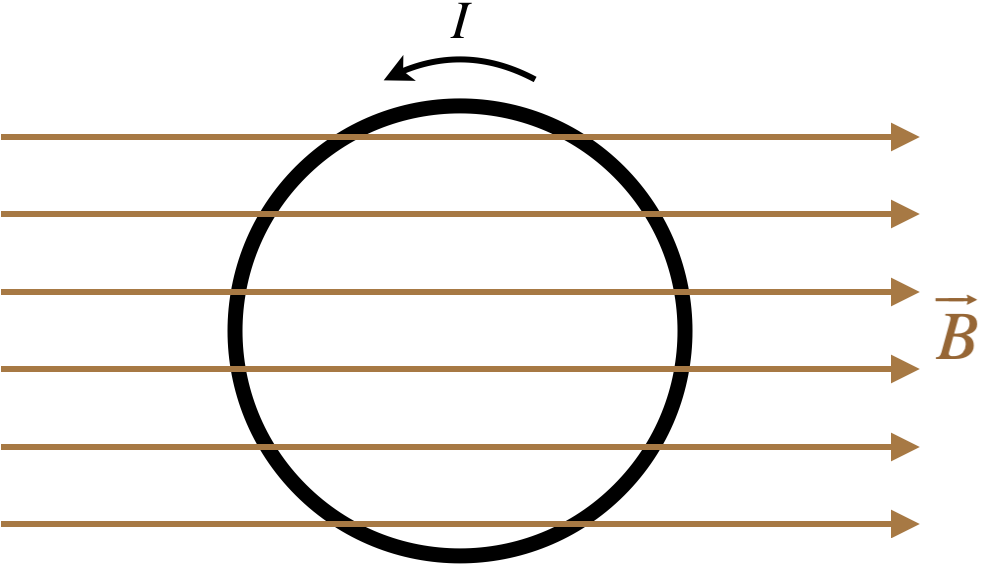
Zoals bij de integratie van ladingsverdelingen om velden te verkrijgen, beginnen we met het invoeren van een coördinatenstelsel (zorg ervoor dat het rechtshandig is, d.w.z.Kies de assen zo dat i maal j = j), selecteer een infinitesimaal stukje van de lus, en beschrijf het in termen van de coördinaten, met een label voor alle variabelen die we onderweg nodig zullen hebben.

Figuur 4.2.2b – Koppel aan een gesloten cirkelvormige lus van draad in een uniform magneetveld

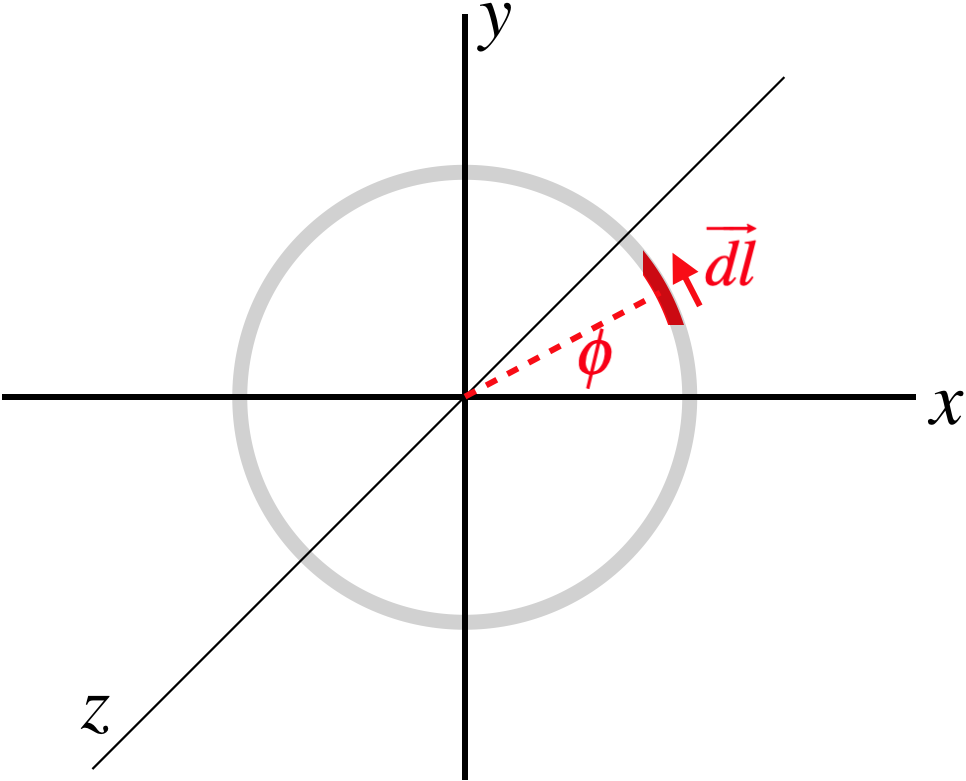
Hier hebben we ervoor gekozen de lus in het xxx y-vlak te plaatsen, en het magneetveld in de xxx-richting. Een oneindig klein stukje draad is gekozen onder een hoek ⁰(⁰) omhoog van de ⁰(+x)-as.

Daarna moeten we de vector ⁰(⁰overrechts) mathematisch uitdrukken. De grootte is de lengte van een infinitesimaal boogsegment, dat is ⁰(R⁰;d⁰). De richting is lastiger te bepalen, maar door het plaatje op te blazen en een beetje meetkunde toe te passen, kunnen we de componenten bepalen:

Figuur 4.2.3 – De huidige elementvector schrijven

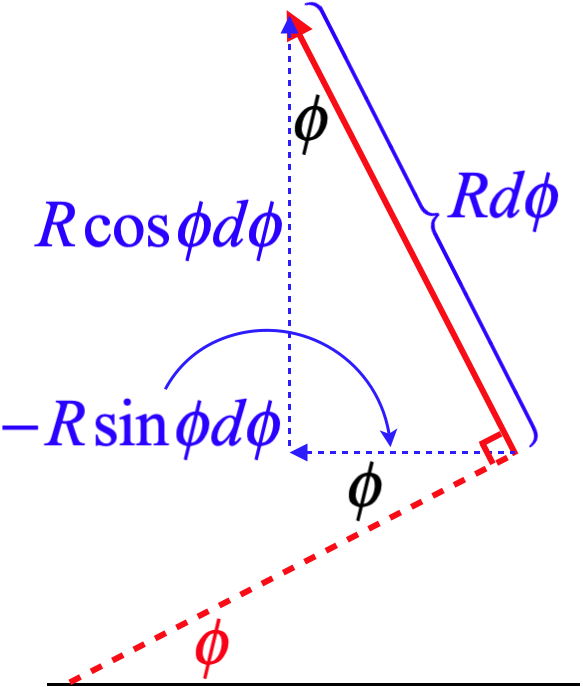
Het samenvoegen tot één vector:

We hebben nu alles wat we nodig hebben. Hoe gecompliceerd de geometrie ook is met de kracht en vervolgens het koppel, we hoeven het niet te volgen – we hoeven alleen maar de vectorwiskunde goed uit te voeren. Bijvoorbeeld, de kracht op het huidige element is:

Met behulp van de kruisproducten van eenheidsvectoren uit Natuurkunde 9A, vullen we \(\widehat i = 0) en \(\widehat j\timeswidehat i = -widehat k\) in, en de kracht op dit element wordt:

Om het koppel te krijgen, kiezen we de oorsprong als referentiepunt, en berekenen de infinitesimale bijdrage aan het koppel rechtstreeks. Door de positievector in te voeren en vectoren te rekenen krijgen we:

Alles wat overblijft is het optellen van alle bijdragen aan het koppel, wat inhoudt dat we integreren over de hoek \(\phi) vanaf \(\rightarrow 2\pi):

= IR^2B_Links=Iinks(\pi R^2RECHTS)B;\widehat j]

Zeker, de grootte van het koppel komt uit op \(\mu;B), waarbij \mu=IA\). En als we de rechterhand-regel gebruiken om de richting van het magnetisch moment te bepalen (uit de bladzijde), gevolgd door de richting van het koppel uit de rechterhand-regel toegepast op (\mu=IA), bevestigen we dat de richting ook werkt.

Dit probleem leek erg lastig omdat de richting van \overrightarrow {dl} overal op de cirkel verandert, maar als deze vector eenmaal is geschreven in termen van \(\) en de eenheidsvectoren, doet de wiskunde de rest!