17.2 Gecombineerde geleiding en convectie

Volgende: 17.3 Dimensieloze Getallen en Up: 17. Convectieve Warmteoverdracht Previous: 17.1 De Reynolds Analogie Inhoudsopgave

We kunnen nu problemen analyseren waarin zowel geleiding als convectie voorkomen, te beginnen met een wand die aan beide zijden gekoeld wordt door stromende vloeistof. Zoals besproken, kan een beschrijving van de convectieve warmteoverdracht expliciet worden gegeven als

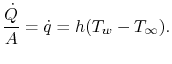
$\displaystyle \frac{\dot{Q}}{A}=\dot{q} = h(T_w-T_\infty).$

Dit zou een model van een turbineblad met inwendige koeling kunnen voorstellen. Figuur 17.6 toont de configuratie.

Figuur 17.6:Geleidende wand met convectieve warmteoverdracht

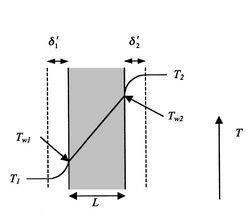
De warmteoverdracht in vloeistof 1 wordt gegeven door

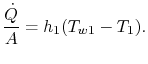
$#displaystyle \frac{Q}}{A} = h_1(T_{w1}-T_1).$

dat is de warmteoverdracht per oppervlakte-eenheid naar de vloeistof. De warmteoverdracht in vloeistof 2 wordt op dezelfde manier gegeven door

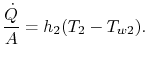
$#displaystyle \frac{\dot{Q}}{A} = h_2 (T_2 -T_{w2}).$

Over de muur heen hebben we

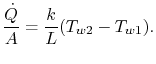
$$\displaystyle \frac{\dot{Q}}{A} = \frac{k}{L}(T_{w2} -T_{w1}).$

De grootheid $\dot{Q}}/A$ is in al deze uitdrukkingen hetzelfde.Door ze allemaal samen te voegen om de bekende totale temperatuurdaling te schrijven, ontstaat een relatie tussen warmteoverdracht en totale temperatuurdaling,:

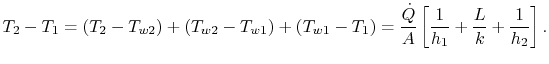$displaystyle T_2-T_1 = (T_2-T_{w2})+(T_{w2}-T_{w1})+(T_{w1}-T_1) ={frac{\dot{Q}}{A}}linkshand.$

(17..20)

We kunnen een warmteweerstand definiëren,, zoals voorheen, zodanig dat

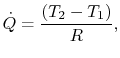
waarbijwordt gegeven door

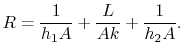$\displaystyle R = \frac{1}{h_1A} + \frac{L}{Ak} + \frac{1}{h_2A}.$

(17..21)

Vergelijking (17..21) is de thermische weerstand voor een massieve wand met convectiewarmteoverdracht aan elke kant.

Voor een turbineblad in een gasturbinemotor is koeling een criticalconsideration. In termen van figuur 17.6 is de verbrandingsuittredetemperatuur (turbine-inlaat) en de temperatuur bij de compressoruittredetemperatuur. We willen $T_{w2}$ vinden, omdat dit de hoogste metaaltemperatuur is. Uit(17.20), kan de wandtemperatuur worden geschreven als

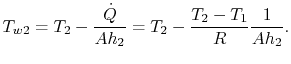$\displaystyle T_{w2} = T_2 - \frac{\dot{Q}}{Ah_2}= T_2 - \frac{T_2 - T_1}{R}\frac{1}{Ah_2}.$

(17..22)

Met behulp van de uitdrukking voor de warmteweerstand, kan de wandtemperatuur worden uitgedrukt in termen van warmtedoorgangscoëfficiënten en wandeigenschappen als

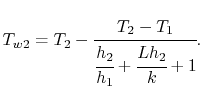$$\displaystyle T_{w2} = T_2 -$

(17..23)

Vergelijking (17.23) geeft een aantal basis ontwerprichtlijnen. Het doel is om een lage waarde van $T_{w2}$ te hebben. Dit betekent datgroot moet zijn,groot moet zijn (maar we hebben wellicht niet veel flexibiliteit in de keuze van het materiaal) enklein moet zijn. Een manier om het eerste te bereiken is doorlaag te houden (bijvoorbeeld door koellucht naar buiten te laten stromen zoals inFiguur 17.1 om het oppervlak af te schermen).

Een tweede voorbeeld van gecombineerde geleiding en convectie wordt gegeven door een cilinder die is blootgesteld aan een stromende vloeistof. De geometrie is weergegeven inFiguur 17.7.

Figuur 17.7:Cilinder in een stromende vloeistof

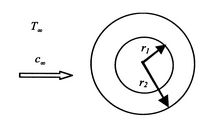
Voor de cilinder wordt de warmteflux aan het buitenoppervlak gegeven door

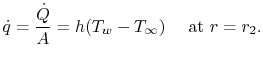$$\displaystyle \dot{q} = \frac{\dot{Q}}{A} = h(T_w-T_infty)\quad \textrm{ at}r=r_2.De randvoorwaarde aan het binnenoppervlak kan een warmtefluxvoorwaarde zijn of een temperatuurspecificatie; wij gebruiken de laatste om de algebra te vereenvoudigen. Dus,$ $ T = T_1$

bij. Dit is een model voor de warmteoverdracht in een pijp met straal, omgeven door isolatie met dikte. De oplossing voor een cilindrisch gebied werd in paragraaf 16.5.1 gegeven als

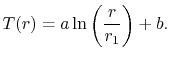
Gebruik van de randvoorwaardelevert.

Op het grensvlak tussen de cilinder en de vloeistof, , zijn de temperatuur en de warmtestroom ononderbroken. (Vraag: Waarom is dit zo? Hoe zou je dit argumenteren?)

$\displaystyle \dot{q} = \underbrace{-k\frac{dT}{dr}}_{{substack{textrm{warmtefl......2}{r_1}rechts)+T_1}rechts)-T_inftyrechts]} _textrm{oppervlaktewarmtestroom naar vloeistof}$

(17..24)

Stoppen van de vorm van de temperatuurverdeling in de cilinder in vergelijking (17..24) levert

24) yields

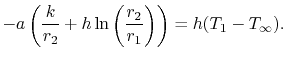
$\displaystyle -a\left(\frac{k}{r_2}+h\ln\left(\frac{r_2}{r_1}\right)\right)=h(T_1-T_\infty).$

De constante van integratie, , is

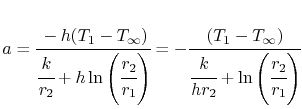
$\displaystyle a=\cfrac{-h(T_1-T_\infty)}{\cfrac{k}{r_2}+h\ln\left(\cfrac{r_2}{r......t)}=-(T_1-T_infty)}{cfrac{k}{hr_2}+h\ln-links(\cfrac{r_2}{r_1}}rechts)}$

en de uitdrukking voor de temperatuur is, in genormaliseerde niet-dimensionale vorm,

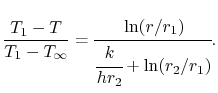(17..25)

De warmtestroom per lengte-eenheid, $\dot{Q}$ , wordt gegeven door

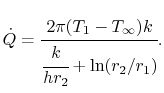$\displaystyle \dot{Q}=\cfrac{2:pi(T_1-T_\infty)k}{\cfrac{k}{hr_2}+\ln(r_2/r_1)}.$

(17..26)

De eenheden in Vergelijking (17.26) zijn W/m-s.

Een interessant probleem is het kiezen van de dikte van de isolatie om het warmteverlies te minimaliseren bij een vast temperatuurverschil tussen de binnenkant van de pijp en de stromende vloeistof ver weg van de pijp. ( $T_1-T_\infty$ is de stuwtemperatuurverdeling voor de pijp). Om het gedrag van de warmtetransfer te begrijpen onderzoeken we de noemer in vergelijking (17.26) als varieert. De dikte van de isolatie die maximale warmteoverdracht geeft, wordt gegeven door

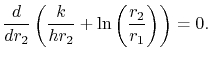$\displaystyle \frac{d}{dr_2}\left(\frac{k}{hr_2}+\ln\left(\frac{r_2}{r_1}\right)\right)=0.$

(17..27)

(Vraag: Hoe weten we dat dit een maximum is?)

Vanuit Vergelijking (17..27)

(Vraag: Hoe weten we dat dit een maximum is?)

Vanuit Vergelijking (17..27)

.27), is de waarde van voor maximum $\dot{Q}$ dus

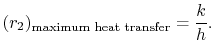(17..28)

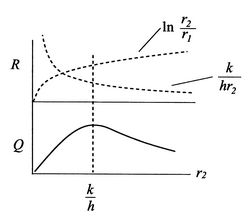
Als kleiner is dan dit, kunnen we isolatie toevoegen en het warmteverlies vergroten. Om te begrijpen waarom dit gebeurt, zie figuur 17.8, die een schematische weergave geeft van de warmteweerstand en de warmteoverdracht. Als toeneemt vanaf een waarde lager dan , treden er twee effecten op. Ten eerste neemt de dikte van de isolatie toe, waardoor de warmteoverdracht daalt omdat de temperatuurgradiënt afneemt; ten tweede neemt de oppervlakte van het buitenoppervlak van de isolatie toe, waardoor de warmteoverdracht toeneemt. Het tweede wordt (losjes) geassocieerd met de term , het eerste met de term $\ln(r_2/r_1)$ . Er zijn dus twee concurrerende effecten die samen een maximum $\dot{Q}$ geven bij .